Trochu optiky na domácej pôde
Ivan Baník, Marcela Chovancová
Abstrakt: Príspevok uvádza niekoľko námetov na jednoduché experimenty z geometrickej optiky. Tie sa dajú realizovať aj v bežných domácich podmienkach. Majú zvýšiť záujem o fyziku a prispieť k eliminácii nežiaducej mechanickej formy štúdia optiky.
Meranie indexu lomu
V ďalšom uvedieme dva stručné návody na meranie indexu lomu vody v domácich podmienkach.
Meranie indexu lomu kvapaliny pomocou ponorenej doštičky
K meraniu potrebujeme nádobu, ktorá má aspoň jednu priehľadnú rovinnú zvislú bočnú stenu. Svetelný lúč vychádzajúci z kvapaliny do vzduchu cez takúto stenu sa láme od kolmice (Obr. 1). K meraniu sa hodí priehľadná sklenená alebo plastová cukornička.
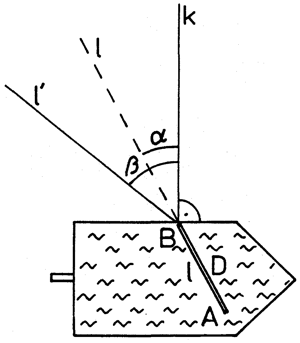
Obr. 1
Do nádoby nalejeme vodu a do nej umiestnime vo zvislej polohe rovinnú doštičku D tak, aby nebola kolmá na rovinnú stenu nádoby a aby jej časť vyčnievala nad úroveň hladiny (Obr.1). Uvedený obrázok znázorňuje situáciu pri pohľade zhora.
Pri pohľade zboku (cez bočnú stenu nádoby) na neponorenú a ponorenú časť doštičky pozorujeme, že skutočný smer doštičky (určený smerom neponorenej časti) je iný, ako zdanlivý smer, aký jej prisúdime pri pozorovaní jej ponorenej časti.
Podrobnejší rozbor ukáže, že uvedené dva smery určujú spolu s kolmicou dopadu k uhol dopadu α a i uhol lomu β. Svetelný lúč mieriaci vo vode vodorovne pozdĺž povrchu ponorenej doštičky by na vzduchu pokračoval v spomenutom zdanlivom smere doštičky. Práve lom svetla spôsobuje, že sa nám smer ponorenej časti doštičky javí odlišný, než je skutočný smer doštičky.
Aby sme uvedené skutočnosti mohli lepšie vyhodnotiť, položíme na stôl papier tak, aby sme na ňom mohli znázorniť jednak rovinné rozhranie voda-vzduch (hrúbku priehľadnej steny nádoby zanedbávame), jednak kolmicu dopadu k, ako aj skutočný a zdanlivý smer doštičky (a teda smer dopadajúceho lúča l a lomeného lúča ľ). Na papieri zmeriame uhol dopadu α a uhol lomu β pre danú polohu doštičky. Na základe zákona lomu určíme index lomu vody. Podobné merania urobíme aj pre ďalšie polohy doštičky vo vode. Za výsledok merania považujeme priemernú hodnotu jednotlivých hodnôt indexu lomu. Na základe vzťahu v = c/n určíme na záver ešte prípadne aj rýchlosť svetla vo vode.
Meranie indexu lomu metódou tieňa
Index lomu vody sa dá zmerať aj v dreze kuchynskej linky. Postup je nasledovný: Postavte do drezu kuchynskej linky, resp. do väčšej prázdnej širšej nádoby, valcovú plechovku džúsu tak, aby ležala na svojej kruhovej základni (Obr. 2). Osvetlite plechovku pomocou nejakého svetelného zdroja vytvárajúceho pomerne ostrý tieň (napr. Slnko, žiarovka bez lustra). Zaznamenajte dĺžku tieňa plechovky na vodorovnom dne prázdnej nádoby. Pridržte plechovku rukou a napusťte do nádoby vodu tak, aby jej hladina nepatrne prevýšila hornú podstavu plechovky. Zistite dĺžku tieňa plechovky na dne v tejto situácii. Vysvetlite prečo nastalo skrátenie tieňa. Zistite, ktoré ďalšie údaje budú potrebné pre výpočet indexu lomu vody. Zmerajte ich. Zo zákona lomu vypočítajte index lomu vody.
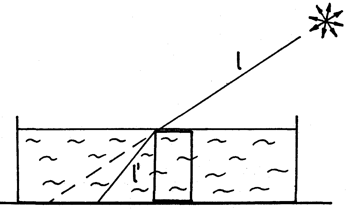
Obr. 2
Totálny odraz
Záhadný kruh na dne
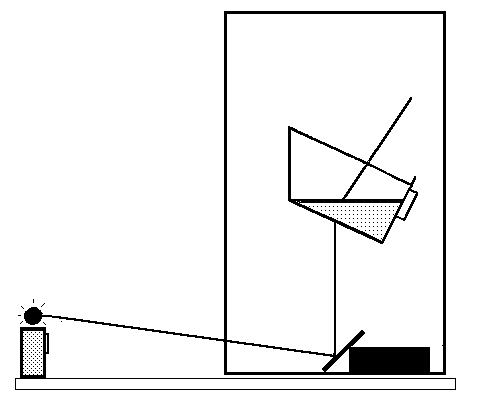
Totálny odraz svetla na rozhraní voda - vzduch sa pozorovateľne prejaví aj pri pokuse s malou svietiacou žiarovkou (4,5 V) ponorenou do vody (Obr. 3). Žiarovke to prakticky nevadí a nevyžaduje to ani elektrickú izoláciu koncov prívodných vodičov. Pokus je vhodné robiť v dreze kuchynskej linky.
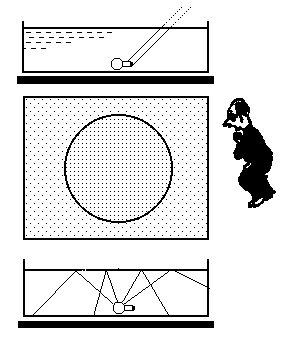
Obr. 3
Svetlo vysielané žiarovkou sa po odraze od rozhrania „voda - vzduch“ vracia z časti na dno. Na dne možno pozorovať zvláštnu kruhovú svetelnú oblasť, ktorá je zaujímavá najmä tým, že jej osvetlenie z vonkajšej strany kruhu je intenzívnejšie, ako zo strany vnútornej. Ide zdanlivo o paradox.
Vysvetlenie javu úzko súvisí s totálnym odrazom. Lúče, ktoré dopadajú na rozhranie voda - vzduch pod menším uhlom dopadu, ako je medzný, sa odrážajú „netotálne“. Časť ich svetelnej energie sa preto dostáva aj nad hladinu. Intenzita odrazeného lúča a teda aj osvetlenie zodpovedajúcej časti dna je preto menšie. Naproti tomu tam, kde ide o totálny odraz, t.j. pri väčších uhloch dopadu svetla na hladinu, bude intenzita odrazených lúčov väčšia. Nuž a v tomto prípade ide o vonkajšok kruhu. Záhadný kruh je teda dôsledkom „ušetrenej energie“ pri uhloch dopadu väčších ako medzný uhol. Ak zmeriame polomer uvažovaného kruhu, hĺbku žiarovky pod hladinou, hĺbku vody v dreze, môžeme analýzou týchto údajov určiť relatívny index lomu vody vzhľadom na vzduch.
Experiment môžeme doplniť aj pozorovaním svetelného kruhu pri postupnom zdvíhaní resp. ponáraní žiarovky. Pri väčšej hĺbke vody sa spomínaný kruh môže zdanlivo stratiť. V skutočnosti ide však len o to, že jeho polomer vzrastie a kruh sa na dno drezu jednoducho nezmestí.
Fyzikálne zákony nie sú teda cudzincami ani v našej kuchyni. Sú pripravené predviesť svoje „fígle“ hoci aj v dreze kuchynskej linky.
Ďalšie pokusy
Tieň a záhada Mesiaca
Ľuďom dlho trvalo, kým pochopili zákonitosti pohybu planét a aj Mesiaca. Je prekvapujúce, že veľmi dlho neprišli na to, že Mesiac je guľatý a že ako guľa svieti iba preto, že odráža slnečné svetlo.
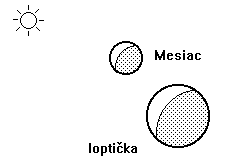
Obr. 4
Pritom je to tak jednoduché... Veď tieň vzniká vďaka priamočiarosti šírenia svetla. Nuž ale, urobte si radšej pokus (Obr. 4): Vezmite ping-pongovú loptičku a v priebehu dňa, keď je na oblohe vidieť súčasne Slnko i Mesiac si ju postavte pred oči s natiahnutou rukou takmer v smere spojnice oko - Mesiac. Čo uvidíte? Nuž bielu guľôčku osvetlenú presne rovnakým spôsobom ako Mesiac. Tá biela guľa, ktorú držíte, bude vykazovať rovnaké fázy ako Mesiac. Rozdiel bude len v tom, že sa to isté nedá pozorovať v noci. To však len preto, že máme krátku ruku a že v noci sme v tieni našej vlastnej Zeme. A tak sa slnečné svetlo na loptičku nedostane. Keby sa mohlo, porovnanie by dopadlo rovnako cez deň.
Pokusy na stene chladničky
Zákonitosti odrazu svetla môžeme sledovať aj na stene chladničky. V prvom rade budeme k tomu potrebovať svetelný lúč. Ako zdroj svetla pre experiment možno použiť valcovú vreckovú elektrickú lampu. Pri pokuse odmontujeme z nej reflektor. Postavíme ju na vrch chladničky tak, aby svietiaca žiarovka prečnievala za okraj. Pod ňu umiestnime papierové tienidlo so štrbinou, ktoré o chladničku držia ferity. Na chladničke sa objaví svetelný lúč vhodný pre experimentovanie. Ako zdroj svetla môžeme využiť aj stolovú lampu postavenú na hornej ploche. Na vymedzenie užšieho svetelného zväzku môžeme použiť aj dve knihy položené na hornej plošine chladničky tak, že ich okraje prečnievajú pred prednú stenu chladničky a tak, že medzi nimi necháme úzku štrbinu.
Lom svetla možno pozorovať aj na stene chladničky (Obr. 5). Pri pokuse použijeme sklenú, alebo plastovú cukorničku, akými bývajú bežne vybavené naše domácnosti. Naplníme ju vodou a pozorujeme prechod svetla sústavou. Ak svetelný lúč dopadá na rozhranie pod nenulovým uhlom dopadu, nastáva lom ku kolmici. Uhol lomu, t.j. uhol medzi lomeným lúčom a kolmicou na hladinu je menší, ako uhol dopadu.
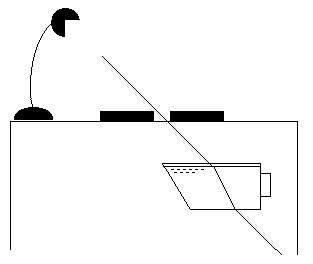
Obr. 5
Pri tomto pokuse využívame vodný hranol vytvorený v sklenej cukorničke pri jej vhodnom naklonení. Pri experimente pozorujeme zmenu smeru, t.j. deviáciu svetelného lúča (Obr. 6). Toto odchýlenie závisí od lámavého uhla hranola. V našom prípade je to uhol medzi vodnou hladinou a dnom cukorničky. Ten meníme nakláňaním cukorničky.
Obr. 6
Pozorované skutočnosti môžeme na stene chladničky vyznačiť zmývateľnou fixkou a potom ich analyzovať z hľadiska dvoch lomov, ktoré pritom nastali. Na stene vyznačíme aj kolmice dopadu a zmeriame „interesantné uhly“. Po prechode svetelného lúča cez planparalelnú vodnú vrstvu v cukorničke (keď je vo vodorovnej polohe) sa - ako možno pozorovať - jeho smer nezmení. Lúč sa však posunie. Je to dôsledok dvojnásobného lomu svetla pri prechode vodnou vrstvou. Pri výstupe lúča z vody nastáva lom od kolmice.
Posunutie lúča na stene chladničky možno pozorovať aj s krabičkou od Tik-Taku, ak ju naplníme vodou a vhodne postavíme lúču do cesty (Obr. 7). Pokus s uvedenou krabičkou sa dá však urobiť aj na papieri na stole. Najprv na papier nakreslíme priamku, ktorá bude reprezentovať dopadajúci lúč. Túto priamku pozorujeme cez naplnenú krabičku, ktorú pritom natáčame do rôznych polôh, čím meníme uhol dopadu lúča na vrstvu. Všímame si, že pozorovaná priamka sa posúva. Predĺženie tejto priamky predstavuje vystupujúci lúč, ktorý môžeme nakresliť na papier tak, že hranu pravítka postavíme v smere pozorovaného obrazu priamky (pri pohľade cez vodnú vrstvu). Posunutie vystupujúceho lúča závisí od uhla dopadu.
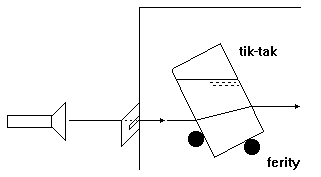
Obr. 7
Literatúra
[1] Baník I., Baník R.: Kaleidoskop učiteľa fyziky. MC Bratislava, 1992-2000
