Historický prístup k zavedeniu stavovej rovnice ideálneho plynu
Peter Horváth
Poďakovanie
Ďakujem Univerzite Komenského v Bratislave za poskytnutie Grantu Univerzity Komenského, z ktorého bola hradená moja účasť na Veletrhu nápadů učielů fyziky v Olomouci.
Úvod
U nás najrozšírenejšia učebnica fyziky pre druhý ročník gymnázia sa k stavovej rovnici ideálneho plynu dopracúva teoretickou metódou (E. Svoboda a kol. 1985, s. 58-70). Využíva a spája poznatky z mechaniky, aplikovať treba poznatky z molekulovej a štatistickej fyziky. Odvodenie je pekné, naozaj treba využiť množstvo dovtedy nadobudnutých poznatkov a schopností. Odvodenie je pre však žiakov náročné a vyžaduje značnú schopnosť myslieť abstraktne. Vyžaduje taktiež matematické zručnosti. Veľká väčšina žiakov tento spôsob výkladu nezvláda. Po zavedení stavovej rovnice sa v učebnici zo stavovej rovnice odvodzujú zákony pre izotermický dej, izochorický dej a izobarický dej. V historickej poznámke sa potom uvádza, že zákony pre izotermický, izochorický a izobarický dej boli najskôr objavené experimentálne.
Teoretický prístup môže viesť u žiakov k pocitu, že fyzika je odtrhnutá od života. Potvrdzovali to odpovede viacerých žiakov v ankete, najmä v kontrolných triedach. Ako príklad teoretického poznatku, bez súvislosti s bežným životom, žiak kontrolnej triedy uviedol práve stavovú rovnicu. Pre žiakov jednoduchší a aj príťažlivejší spôsob zavedenia stavovej rovnice predstavuje empirický prístup. Tento prístup som ako študent prvýkrát videl na seminári z didaktiky fyziky, ktorý viedol V. Koubek (1999, s. 102-103). Empirický prístup navyše sleduje aj historický vývoj, akým sa k stavovej rovnici naozaj prišlo. V článku je uvedená najprv história stavovej rovnice a potom postup na vyučovacej hodine. Na našich hodinách postupujeme opačne, najprv zavedieme pomocou empirického prístupu stavovú rovnicu a o histórii sa so žiakmi porozprávame buď počas realizácie niektorého z experimentov, alebo si ju necháme na neskôr. Ak by sme najprv žiakom hovorili o histórii, prezradili by sme im výsledky, ktoré majú sami objaviť z meraní. Postup je zvolený tak, že žiakom stačia poznatky o plynoch, ktoré majú už z prvého ročníka, čiže ide o prvé hodiny o štruktúre a vlastnostiach plynov v druhom ročníku.
História stavovej rovnice
Ako už bolo spomenuté, zákony pre izotermický, izobarický a izochorický dej boli najprv objavené empiricky a z nich bola potom odvodená stavová rovnica. Jej teoretické odvodenie na základe kinetickej teórie plynov bolo prijaté neskôr. História stavovej rovnice sa zrejme začína u Roberta Boyla. Na základe experimentov, ktoré Boyle uverejnil roku 1660, vyslovil jeho žiak Richard Towneley roku 1662 hypotézu, podľa ktorej tlak vzduchu je nepriamo úmerný jeho objemu (pri danej teplote). Roku 1679 uverejnil podobné výsledky aj Edme Mariotte. Zákon pre izotermický dej dnes nazývame Boylov-Mariottov zákon. Pojem „izotermický dej“ zaviedol až roku 1859 William John Macquorn Rankine.
Teplotnú rozťažnosť vzduchu využíval už Galilei pri konštrukcii svojho teplomeru z roku 1597. Po ňom sa teplotnou rozťažnosťou vzduchu zaoberal Guillaume Amontons, ktorý koncom 17. storočia skonštruoval prvý tlakový plynový teplomer. Prvýkrát určil teplotnú rozťažnosť vzduchu už roku 1787 Jacques Alexandre César Charles, ale o jeho práci sa svet dozvedel až od Gay-Lussaca. Joseph Louis Gay-Lussac a John Dalton publikovali roku 1802 nezávisle od seba presné merania koeficientu teplotnej rozťažnosti vzduchu. Pri meraní teploty využíval Gay-Lussac Celsiovu stupnicu. Zaujímavosťou Celsiovej stupnice je, že Celsius ju najprv zaviedol otočenú, 0 °C zodpovedala teplota varu vody a 100 °C zodpovedala teplota tuhnutia vody. Dnešné ciachovanie Celziovej stupnice pochádza od Celsiovho žiaka Martina Strömera. Gay-Lussac ukázal, že rovnaký koeficient teplotnej rozťažnosti ako vzduch majú kyslík, dusík, oxid uhličitý a iné plyny. Podľa Gay-Lussaca pre objem (ideálneho) plynu V pri teplote t v °C platí:
![]() ,
,
kde V0 je objem plynu pri 0 °C a γ je koeficient tepelnej rozťažnosti plynu. Daná rovnica predstavuje jednu z možných matematických formulácií Gay-Lussacovho zákona pre izobarický dej. Pri teplote ![]() sa objem plynu podľa Gay-Lussaca rovná nule. Táto teplota predstavuje absolútnu teplotnú nulu. Na základe svojich meraní určil Gay-Lussac absolútnu nulu pri teplote –267 °C.
sa objem plynu podľa Gay-Lussaca rovná nule. Táto teplota predstavuje absolútnu teplotnú nulu. Na základe svojich meraní určil Gay-Lussac absolútnu nulu pri teplote –267 °C.
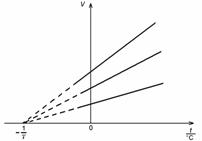
Obr. 1 Závislosť objemu plynu od teploty
Ďalšie závery z Gay-Lussacových výskumov publikoval roku 1811 Amadeo Avogadro, ktorý okrem iného zaviedol pojem molekula a vyslovil vetu, podľa ktorej je v rovnakých objemoch plynných látok pri danom tlaku a objeme rovnaký počet molekúl.
Stavovú rovnicu ideálneho plynu odvodil kombináciou Boylovho-Mariottovho zákona a Gay-Lussacovho zákona roku 1824 Sadi Nicolas Léonard Carnot. Jeho zápis spresnil roku 1834 Clapeyron, Clapeyronov zápis bol
![]() ,
,
kde p je tlak V je objem plynu, R je univerzálna plynová konštanta a t je teplota v °C.
Presnejšie merania absolútnej nuly urobil v r. 1837 Fredrik Rudberg a v roku 1840 Gustav Heinrich Magnus. Ďalšie merania uskutočnil v rokoch 1840 až 1842 Henri Victor Regnault, ktorý určil absolútnu nulu na –272,75 °C a prišiel k záveru, že plynové teplomery s rôznymi plynmi neposkytujú rovnaké hodnoty pri meraní teploty a že stavová rovnica platí pre reálne plyny iba približne. Neexistujúci plyn, pre ktorý táto rovnica platí presne, nazval dokonalým plynom. Roku 1848 navrhol Wiliam Thomson (Lord Kelvin) absolútnu termodynamickú teplotnú stupnicu, ktorá nezávisí od použitej teplomernej látky. Úpravami tejto stupnice v roku 1854, ktorú vykonali Thomson a James Prescott Joule, a definitívnou úpravou až v roku 1954 bola zavedená dnes používaná termodynamická teplotná stupnica, kde teplotu meriame v kelvinoch.
Čo sa týka teoretického odvodenia, roku 1738 Daniel Bernoulli odvodil vzťah pre tlak plynu zo zmeny hybnosti častíc narážajúcich na steny nádoby. Svojím odvodením predbehol dobu o vyše 100 rokov. Tú istú úvahu ako D. Bernoulli použil roku 1857 Rudolf Clausius. Roku 1862 zaviedol Clausius pojem ideálny plyn a stavovú rovnicu molu ideálneho plynu napísal v tvare
![]() ,
,
kde p je tlak, V je objem, R je univerzálna plynová konštanta a T je teplota meraná na termodynamickej stupnici, ktorú zaviedol Kelvin. Informácie o histórii stavovej rovnice a histórii Kelvinovej stupnice sú spracované z práce R. Zajaca a J. Šebestu (1990) a z práce R. Zajaca a J. Chrapana (1986, s. 49-51).
Priebeh hodiny
V súlade s historickým kontextom budeme uskutočňovať so žiakmi sériu experimentov. Učivo je v súčasných osnovách zaradené na gymnáziu do druhého ročníka. Už v prvom ročníku pri rozvíjaní pojmu tlak predvádzame pokusy demonštrujúce atmosférický tlak. Veľmi populárne sú napríklad demonštrácie pomocou vývevy, ako nafúknutie balónika pod zvonom vývevy, žiakom sa páčia Magdeburské pologule.
Pred odvodením stavovej rovnice si tieto pokusy v druhom ročníku zopakujeme. Pohráme sa aj s jednoduchým teplomerom, ktorý využíva teplotnú rozťažnosť plynu (obrázok 2) a PET fľašou s uzavretým vzduchom, ktorú umiestnime do chladničky, alebo ak je vonku zima, tak von. Fľaša sa v chladnom prostredí stiahne.

Obr. 2 Slečna drží v ruke jednoduchý teplomer využívajúci teplotnú rozťažnosť vzduchu
Aj pri samotnom odvodzovaní stavovej rovnice postupujeme na základe experimentov, v súlade s historickým kontextom. Podobne ako v histórii, začneme aj my izotermickým dejom. Pri meraniach môžeme využiť počítač. Plyn, v našom prípade vzduch, uzavrieme do striekačky a na jej koniec pripojíme tlakový snímač. Na obrazovke necháme zobrazovať tlak v striekačke. Striekačka má stupnicu s hodnotami objemu. Pri stlačení plynu v striekačke narastie tlak, pri zväčšení objemu plynu v striekačke tlak klesá. Hodnoty si zaznamenávame do počítača a hneď si ich aj nechávame vykresľovať do grafu (obr. 3). Po skončení merania vyzveme žiakov: „Skúste zistiť zákonitosť, vzťah medzi nameranými hodnotami.“ Z grafu žiaci poľahky určia, že medzi tlakom a objemom uzavretého plynu v striekačke bola nepriama úmernosť. Takto sme odvodili Boylov-Mariottov zákon:
![]() ,
,
resp.
![]() ,
, ![]() ,
,
kde p je tlak plynu, V je jeho objem a konšt1 je konštanta. Platnosť tohto vzťahu si žiaci overia tak, že príslušné dvojice číselných hodnôt tlaku a objemu navzájom vynásobia. Pre každú z vynásobených dvojíc dostanú (takmer) rovnaké čísla.
Pre dva stavy uzavretého plynu, ktorého teplota sa nemení, ale mení sa objem, a tým aj tlak, teda platí: ![]()
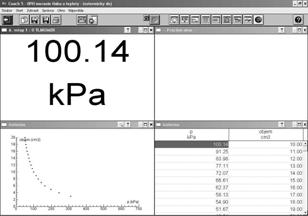
Obr. 3 Obrazovka počítača po skončení merania izotermického deja
Teraz pristúpime k izochorickému deju. Izochorický dej budeme skúmať so vzduchom uzavretým v sklenenej banke, ku ktorej opäť pripojíme pomocou hadičky tlakový snímač. Banku umiestnime do rýchlovarnej kanvice so studenou vodou. Do vody v rýchlovarnej kanvici umiestnime ešte teplotný snímač, taktiež pripojený k počítaču (obr. 4).
Experiment nastavíme tak, aby sa nám na obrazovke zobrazoval graf závislosti tlaku od teploty, prípadne spolu s ním aj okamžité hodnoty tlaku v banke a teploty vody v kanvici. Predpokladáme, že teplota vzduchu v banke sa rovná teplote vody v kanvici. Pri meraní teploty používame, rovnako ako Gay-Lussac, z bežného života známu Celsiovu stupnicu.

Obr. 4 Nádobku a teplotný snímač umiestnime do rýchlovarnej kanvice
Začneme meranie, zapneme kanvicu. Na obrazovke sa začne vykresľovať graf závislosti tlaku a teploty vzduchu v banke (obr. 5). Kým sa nám zohrieva voda v kanvici, môžeme využiť čas na žiacke otázky, alebo môžeme žiakom porozprávať o vzniku Celsiovej a Kelvinovej stupnice. Meranie skončíme pri teplote 80 až 90 °C a vypneme kanvicu.
Z nameraného grafu jasne vidno, že závislosť medzi tlakom a teplotou uzavretého plynu je lineárna. Náš graf však sa nezačína v bode 0. Čo keby sme plyn nezohrievali, ale ochladzovali. Teplota by zrejme klesala. Dokedy by klesala? To už sa dopracúvame k absolútnej teplotnej nule, podobne ako Gay-Lussac (len na grafe s tlakom, nie s objemom), čo je podľa môjho názoru najkrajšia časť tohto merania (obr. 6).
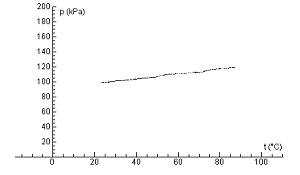
Obr. 5 Závislosť medzi tlakom a teplotou uzavretého plynu, spracovaná pomocou programu Coach 5
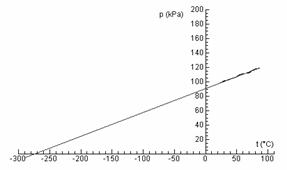
Obr. 6 Lineárnou aproximáciou sa pri tlaku 0 kPa dostaneme k absolútnej teplotnej nule
V mieste, kde predĺženie grafu pretne teplotnú os, krásne vychádza približná hodnota absolútnej teplotnej nuly. Aby sme závislosť medzi tlakom a teplotou zapísali čo najkrajšie a matematicky čo najjednoduchšie, oplatí sa nám nahradiť Celsiovu stupnicu inou, takou, ktorá sa začína v absolútnej teplotnej nule. Preto je vhodné zaviesť Kelvinovu stupnicu. Z nášho grafu (približne) vidno, kde sa začína Kelvinova stupnica. Teraz už môžeme napísať Charlesov zákon v tvare:
![]() ,
,
alebo
![]() ,
,
alebo
![]() .
.
V týchto vzťahoch je p tlak, T termodynamická teplota a žiakom treba dobre zdôrazniť, že tu vystupuje iná konštanta ako pri izotermickom deji, preto označujeme konštantu indexom 2. Pre dva stavy toho istého plynu, ak sa nemení objem plynu, môžeme napísať:
![]() .
.
K stavovej rovnici sa možno dopracovať jednoduchými úvahami. Pre izotermický dej sme našli vzťah:
![]() .
.
Teplota sa nemení. Čiže môžeme napísať aj:
![]() ,
,
a pretože na pravej strane vystupujú dve konštanty, konšt1 a teplota T, možno napísať:
![]() .
.
Podobne sme pre izochorický dej našli vzťah
![]() .
.
V tomto prípade sa nemenil objem, teda možno napísať:
![]() ,
,
a pretože na pravej strane vystupujú dve konštanty, konšt2 a objem V, možno napísať:
![]() .
.
Vidíme, že pre oba deje platilo ![]() , čo je matematická formulácia stavovej rovnice ideálneho plynu. Táto platí pre akékoľvek prechody plynu z jedného stavu do druhého za predpokladu, že nám plyn neuniká, alebo sa jeho hmotnosť nezväčšuje.
, čo je matematická formulácia stavovej rovnice ideálneho plynu. Táto platí pre akékoľvek prechody plynu z jedného stavu do druhého za predpokladu, že nám plyn neuniká, alebo sa jeho hmotnosť nezväčšuje.
Ostáva ešte prediskutovať, od čoho ešte závisí tlak, ak fixujeme objem a teplotu? Napríklad hustíme koleso alebo basketbalovú loptu. Ich teplota sa výrazne nemení, ani ich objem, ale tlak narastá. Teda tlak plynu závisí ešte aj od množstva plynu v uzavretej nádobe.
![]() ,
,
kde N je počet častíc plynu. Preto môžeme stavovú rovnicu spresniť:
![]() ,
,
kde k je Boltzmannova konštanta.
4 Organizačné poznámky a didaktický komentár
Ešte pred hodinou venovanou zavedeniu stavovej rovnice sa naozaj oplatí zopakovať si so žiakmi pokusy demonštrujúce atmosférický tlak a pokusy na teplotnú rozťažnosť vzduchu. Takisto treba pred odvodením stavovej rovnice zaviesť príslušné stavové veličiny, ale nie je nutné pripomínať termodynamickú Kelvinovu stupnicu. Tá sa nám pri analýze pokusu krásne ponúkne sama. Ako sme spomínali v úvode, najprv zavedieme pomocou empirického prístupu stavovú rovnicu a o histórii sa so žiakmi porozprávame buď počas realizácie niektorého z experimentov, alebo si ju necháme na neskôr, aby sme neprišli o možnosť samostatného žiackeho objavovania závislostí.
Meranie izochorického deja je možné aj zrýchliť, a to tak, že si dopredu pripravíme niekoľko nádob, asi 8, s vodou s teplotami od 15-20°C do 80-90°C. Banku so vzduchom potom postupne ponárame do pripravených nádob s vodou, pričom meriame teplotu vody a tlak v nádobe. Zo získaných príslušných dvojíc vyhotovíme tabuľku a graf.
Meranie izotermického a izochorického deja pripravíme na delenú hodinu, kde je polovica žiakov z triedy. Samotné merania izotermického a izochorického deje sa dajú stihnúť na jednej hodine. Počítač s príslušenstvom a pomôcky si treba dopredu pripraviť a vyskúšať, aby na hodine nevznikli časové straty kvôli technickým problémom. Pri samotnom meraní treba dať pozor, aby banka bola celá ponorená vo vode a zároveň, aby sa nedotýkala výhrevného telesa. Banku zvykneme zaťažovať kovovou obrúčkou, aby nestúpala nahor, a cez hadičku, ku ktorej je pripojený senzor, ju vrchnákom kanvice pridržiavame, aby neklesla úplne dolu k výhrevnému telesu. Podobne ani teplotný snímač sa nemá dotýkať výhrevného telesa.
Ak všetko dobre vychádza, dá sa na hodine stihnúť aj odvodenie stavovej rovnice. Je to však pre žiakov veľa informácií naraz. Preto sa zvykneme na nasledujúcej hodine k výsledkom merania a ich dôsledkom vrátiť a pozrieť sa na ne ešte raz pomaly.
Namiesto počítačových snímačov môžu žiaci použiť obyčajný teplomer a lekársky tlakomer. Lekársky tlakomer dostať kúpiť v zdravotníckych potrebách, slúži na meranie tlaku krvi (obrázky 7, 8). Nemusíme kupovať celú súpravu na meranie krvného tlaku (cca 900 Sk), stačí nám náhradný diel z tejto súpravy, samotný tlakomer (cca 250 Sk).
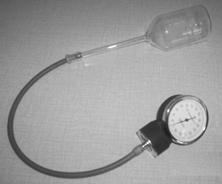
Obr. 7 Súprava zapojená na meranie izochorického deja s lekárskym tlakomerom.
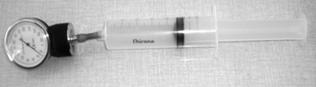
Obr. 8 Súprava zapojená na meranie izotermického deja s lekárskym tlakomerom.
Pri meraní lekárskym tlakomerom sa žiaci naučia rozpoznávať jednotku tlaku, používanú v medicíne. Ide o milimeter ortuťového stĺpca (mmHg, 1 mmHg = 133,322 Pa, čo je 1 Torr). Pri meraní potom treba túto jednotku premeniť do sústavy SI, kde je jednotkou tlaku pascal. Uvedomiť si treba aj to, že nulu ukazuje tento tlakomer pri atmosférickom tlaku, čiže meria vlastne pretlak oproti atmosférickému tlaku. Teda k odmeranému tlaku po premene na pascaly (alebo kilopascaly) treba ešte pripočítať atmosférický tlak, približne 100 kPa. Pri meraní izotermického deja treba dať pozor, aby sme príliš silno nestláčali striekačku a nepoškodili si tak tlakomer prekročením jeho rozsahu. Ak máme teplomerov a tlakomerov viac, meranie môžu uskutočňovať sami žiaci v skupinkách a výsledky si navzájom porovnať, prípadne spojiť. Takto môžeme rozvíjať kompetencie realizovať experiment, napísať o ňom zápis, zapísať výsledky meraní graficky. Z grafov získavať nové informácie, navrhovať hypotézy, hľadať a matematicky formulovať funkčné závislosti medzi veličinami.
V praxi sa nám potvrdzuje, že pre žiakov je historicko-empirický prístup k zavedeniu stavovej rovnice ľahší ako teoretické odvodenie z kinetickej teórie. Ak má niekto zo žiakov záujem, môže si teoretický prístup pozrieť doma. Dobrú známku si vyslúži žiak, ktorý si sám naštuduje odvodenie z učebnice a vysvetlí ho spolužiakom na hodine.
Po odvodení stavovej rovnice je vhodné žiakov upozorniť na poznávací postup vo fyzike. Na začiatku je experiment a meranie. Z nich bol empiricky odvodený zákon. Neskôr bol zákon vysvetlený na základe hypotézy o mechanizme deja (teoretické odvodenie). Hypotéza bola overená pomocou odvodenia dôsledkov z nej vyplývajúcich (väčšie množstvo plynu v uzavretej nádobe spôsobí zvýšenie tlaku).
Literatúra
Koubek, V: Fyzikálne experimenty a modely v školskom mikropočítačom podporovanom laboratóriu. Bratislava : Matematicko-fyzikálna fakulta Univerzity Komenského, 1999. ISBN 80-223-1232-0
Svoboda, E. a i.: Fyzika pre 2. ročník gymnázia. 1. vyd. Bratislava : SPN, 1985.
Zajac, R., Chrapan, J.: Dejiny fyziky. Vysokoškolské skriptá. Bratislava : Matematicko-fyzikálna fakulta Univerzity Komenského, 1996.
Zajac, R., Šebesta, J.: Historické pramene súčasnej fyziky 1, Od Aristotela po Boltzmanna. Bratislava : Alfa, 1990. ISBN 80-05-00231-9
