Ladička, jak ji neznáte
Leoš Dvořák
Příspěvek ukazuje, jak lze obměnit či jinak využít některé známé pokusy s ladičkou a jak jednoduchá otázka, týkající se útlumu ladičky, může vést k zajímavému měření a k možná trochu překvapivým úvahám.
Úvod: ladička, jak ji známe i neznáme
Ladička je známá pomůcka, kterou alespoň někdy využije asi většina učitelů. Užíváme ji jako zdroj známé frekvence (většinou komorního a, tedy 440 Hz), k demonstraci rezonance (úderem rozezníme jednu ladičku s rezonanční skříňkou, od ní se rozezní druhá blízká ladička), k demonstraci rázů (když u jedné ladičky přívažkem snížíme frekvenci) i k dalším demonstracím a měřením. Příkladem může být měření rychlosti zvuku pomocí otevřené či na jednom konci uzavřené trubice, popsané například v učebnici [1] ve Cvičení 3 v závěru knihy. Můžete si říci – co dalšího by ještě šlo s ladičkou provádět či co by na ní šlo zkoumat?
Bližší pohled a nahlédnutí do literatury nás přesvědčí, že ladička není tak jednoduchý objekt, jak by se mohlo zdát. Zdaleka nekmitá jen jedním způsobem či na jediné frekvenci. Udeříme-li do ladičky zhruba v polovině ramene tvrdším, třeba kovovým předmětem, uslyšíme zpočátku jasně zvonivý zvuk o výrazně vyšší frekvenci než zmíněných 440 Hz. A sama o sobě, bez rezonanční skříňky, nejenže zní slabě, ale to, do kterých směrů jak silně vyzařuje zvuk, je velice zajímavým problémem. Více se o těchto otázkách můžeme poučit například v článcích [2] a [3]. Ovšem časopis American Journal of Physics, v němž byly publikovány, je zaměřen na vysokoškolskou výuku fyziky. Středoškolské fyzice na pokročilejší úrovni by mohl být bližší článek [4] o experimentech s ladičkou využívajících počítač. Daný článek také svým datem ukazuje, že ani ve výuce fyziky ve světě není ladička zaprášenou a odloženou veteší.
Podívejme se však raději na pokusy a úvahy co nejjednodušší, opravdu využitelné na střední a zčásti i na základní škole. Některé z těchto experimentů již léta s dobrým ohlasem používám v demonstračních pokusech pro žáky SŠ i ZŠ; několik závěrečných měření a úvah (byť samozřejmě nemohu ručit za jejich „světovou originalitu“) má zde premiéru.
Známé pokusy v novém hávu
Jak rozezpívat ladičku
Jak rozeznít ladičku? Samozřejmě úderem, zvukem jiné ladičky o stejné frekvenci nebo tónem z reproduktoru. Do reproduktoru můžeme pouštět zesílený signál ze signálního generátoru, s výhodou však můžeme využít i počítač. Použít můžeme například generátorů ve volně dostupném programu Sound Card Scope. (Lze jej stáhnout z webové adresy [5]; je též k dispozici na CD [6].) S reproduktorovými skříňkami připojenými k počítači můžeme ladičku bez problémů rozeznít na 440 Hz a také ukázat, že tóny jiných frekvencí (např. 430 či 450 Hz) ji nerozeznějí.
Efektní variantou tohoto pokusu je rozeznít ladičku hlasem, tedy opravdu ji „rozezpívat“. Zpívat je třeba do otvoru rezonanční skříňky, poměrně hlasitě a samozřejmě se správnou výškou tónu. Stačí normální „lááá“. V nácviku velmi pomáhá držet skříňku za dřevěnou část, do níž je zasunuta ladička. Když se „strefíme“ do správné výšky tónu, cítíme v ruce zřetelné chvění.
(Poznámka: Pánové, kteří mají hlas posazen níž a nezvládnou komorní a ani falsetem, nemusí být ztraceni. Při zpěvu o oktávu níž mohou zkusit ladičku rozeznít „druhou harmonickou“ zpívaného tónu.)
Ladička, kulička a „trouby z Jericha“
Poměrně známý je pokus, při němž se lehká kulička zavěšená na tenkém vlákně (niti) zlehka dotýká ramene ladičky. Když ladička kmitá, rameno „odcvrnkává“ kuličku, která se nakonec viditelně kýve.
Ne každý učitel ovšem využívá tento pokus ve spojení s předchozím – tedy tak, že ladičku rozezní nikoli úderem, ale rezonancí, pomocí zvuku druhé ladičky. Tento pokus je efektní, zejména pokud máme ladičky a skříňky v takovém stavu, že se rozezní i na vzdálenost několika metrů. (Záleží samozřejmě i na akustice třídy; navíc kulička se musí ramene ladičky dotýkat opravdu jen velmi zlehka, ale přitom mezi ní a ramenem nesmí být mezera.)
Možnost rozkývat kuličku na dálku se většinou žákům líbí. Tento pokus však stojí za to okomentovat podrobněji. Je totiž důkazem, že zvuk přenáší energii. Na začátku pokusu visí kulička nehybně dolů. Na konci se kýve, má tedy zjevně větší energii. Jak jsme jí energii dodali? Nikoli přímým úderem, udeřili jsme přece do druhé ladičky, té jsme dodali energii. Na ladičku u kuličky přenesl energii zvuk!
S nadsázkou lze dodat, že kdyby ladička byla velmi velká a kdybychom místo kuličky měli zavěšenou kouli na bourání, mohli bychom takto bourat zdi. Přitom můžeme připomenout i legendu o hradbách Jericha zbořených zvukem trubek…
Jak se ladička tlumí aneb k čemu je rezonanční skříňka
Ladička s rezonanční skříňkou zní podstatně hlasitěji než bez ní. Ptáme-li se proč, narazíme často na vágní odpovědi typu „rezonanční skříňka zesiluje zvuk“. Zeptáme-li se jak zesiluje zvuk, když nemá žádné zdroje energie, dostaneme leckdy odpověď, že „rezonancí“, což je ještě mlhavější. (Laskavý čtenář se na tomto místě může zamyslet, nakolik je mu otázka zesílení zvuku rezonanční skříňkou jasná. Odkud se bere energie potřebná k tomu, aby ladička se skříňkou zněla hlasitěji?)
Se skříňkou nebo bez ní? (Provokativní otázka)
Pomůže nám následující otázka ([7]), kterou lze žákům předložit jako problém:
Rozezníme ladičku úderem a budeme měřit čas, dokud ji budeme slyšet. Ladičku přitom můžeme mít pár centimetrů od ucha. Uděláme tento pokus s ladičkou bez skříňky a s rezonanční skříňkou. Kdy ji budeme slyšet déle?
a) bez skříňky b) se skříňkou c) stejně dlouho
Žáky lze nechat odhadnout výsledek pokusu a nechat o něm hlasovat. Odhady se různí, většinou převládá názor, že déle uslyšíme ladičku se skříňkou.
Zkuste si tento pokus sami, někde v hodně tichém prostředí. Nejprve třeba s ladičkou se skříňkou. Skříňku je lépe položit na stůl. (Držíme-li ji, ladičku obvykle více tlumíme.) Zvuk slyšíme překvapivě dlouho, až kolem jedné minuty. Záleží samozřejmě na ladičce i na rezonanční skříňce, s některými ladičkami to může být půl až ¾ minuty, s jinými výrazně přes minutu. S ladičkou bez skříňky, drženou volně v ruce, je to podstatně déle – u ladiček, které jsem zkoušel já, to bylo dvě až tři minuty!
Takže „a) je správně“! A na základě úvah o energii lze jednoduše pochopit, proč je tomu tak. Úderem jsme dodali ladičce energii. Ladičku bez skříňky trochu tlumíme rukou, ale ne příliš. Dále se ladička tlumí tím, že rozkmitává vzduch kolem sebe a předává mu energii. Ale ramena ladičky jsou malá, vzduch nerozkmitávají příliš efektivně. Proto je zvuk slabý – a proto také energie z ladičky odchází pomalu a ladičku slyšíme déle.
Naproti tomu rezonanční skříňka je konstruována tak, aby co nejefektivněji předávala kmity okolnímu vzduchu. (Profesionální akustici by zde patrně mluvili o věcech jako přizpůsobení impedancí.) Tedy, jednoduše řečeno, rezonanční skříňka účinně „odsává“ energii z ladičky a předává ji okolnímu vzduchu. Proto ji slyšíme hlasitě – ale právě proto se také kmity dříve utlumí.
Měříme útlum ladičky
Výše popsaný pokus se nehodí k demonstraci pro celou třídu. Jednak zde ruší všudypřítomný šum, jednak je při pokusu opravdu dobré mít ucho dostatečně blízko – a i kdybychom nechali poslouchat jen jednoho žáka, je otázkou, zda bude mít celá třída trpělivost tiše na něj zírat přes dvě minuty.
Pomoci nám může počítač. Tedy počítač se zvukovou kartou a mikrofonem, ale to je dnes pomalu již vybavení patřící k „jednoduchým pomůckám“. Zvuk můžeme nahrát a analyzovat pomocí volně šiřitelného programu Audacity. (Tento program lze stáhnout ze stránek [8]. Velmi stručný popis jeho nejzákladnějšího ovládání a některých možností jeho využití lze najít v článku [9].) Tento program nám umožňuje nahrát postupně zvuk ladičky se skříňkou a bez skříňky a porovnat průběh amplitudy obou kmitů.
Obrázek 1 ukazuje, jaké výsledky můžeme naměřit. Ukazuje „obálku“ kmitů, tedy pokles amplitudy v čase 10 s až 80 s ;po úderu do ladičky. (Ve skutečnosti je dolní graf ukazující kmity ladičky bez skříňky poněkud posunut, aby ukazoval zhruba stejnou počáteční amplitudu jako horní graf kmitů ladičky se skříňkou. „Zvlnění“ dolního grafu je dáno zřejmě tím, že držíme-li ladičku v ruce blízko mikrofonu, ovlivňují hlasitost snímanou mikrofonem i drobné změny polohy ladičky.)
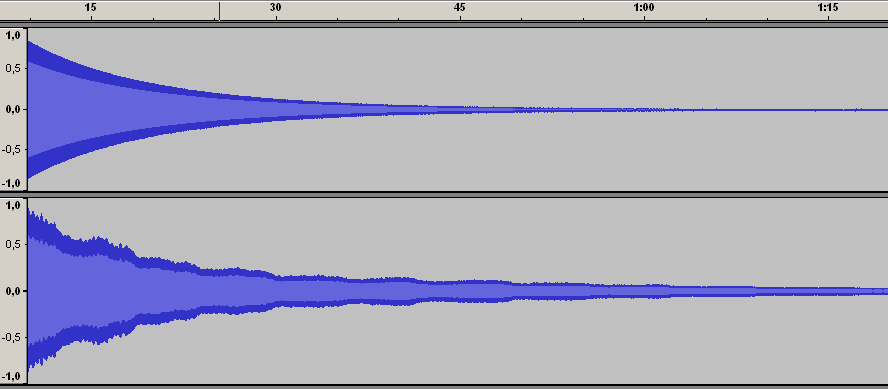
Obr. 1 Útlum zvuku ladičky se skříňkou (horní graf) a bez skříňky (dolní graf)
Snad ještě lépe lze útlum ladiček srovnat, zobrazíme-li amplitudy v logaritmické škále, tedy v decibelech. Exponenciální pokles amplitudy viditelný na obr. 1 se v logaritmické škále zobrazí jako lineární pokles, jak to ukazuje obr. 2.
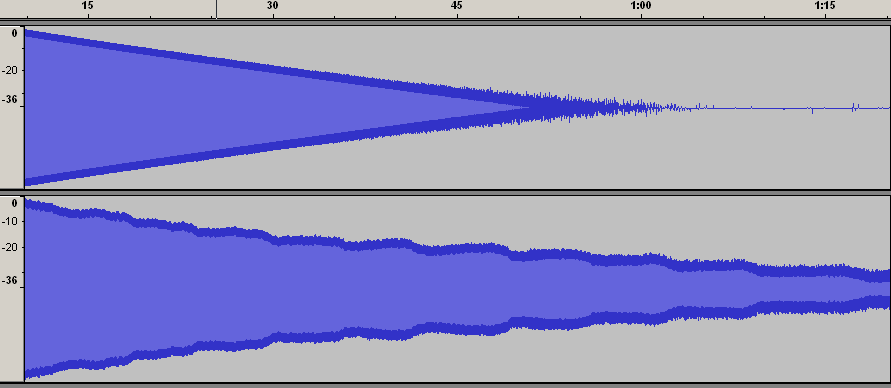
Obr. 2 Útlum ladiček při zobrazení amplitud v logaritmické škále (v decibelech)
Přestože daná zobrazení jsou velmi názorná, pro přesnější měření je výhodné využít ještě další možnost, kterou Audacity nabízí, a to zobrazení spektra signálu. Jak ukazuje obr. 3, v zobrazeném spektru lze velmi dobře vidět „pík“ odpovídající zvuku ladičky a odlišit jej od ostatních zvuků a šumů okolí. Nastavíme-li kurzor na frekvenci ladičky, můžeme přímo odečíst hlasitost v decibelech. Jde sice samozřejmě jen o relativní hodnotu (ne o absolutní hlasitost v decibelech), ale pro měření útlumu nám to stačí. Výhodou je, že takto můžeme určit hlasitost ladičky i v případech, kdy v normálním zobrazení kmitů (v závislosti na čase) se již signál ladičky „utápí v šumu“. Ve spektru pík na frekvenci 440 Hz stále ještě dobře rozlišíme.
Obrázek 3 ukazuje i to, jak přizpůsobit některá nastavení okna pro zobrazení spektra. Je třeba zvolit vyšší počet bodů, z nichž se spektrum počítá (v našem případě 8192), a logaritmickou škálu frekvencí. Než zadáme programu Audacity vykreslit spektrum (je to v položce menu Analyzovat), vybereme myší časový interval, v němž se má spektrum určit. (Já jsem volil kraje intervalu o 0,1 s od střední hodnoty, tedy např. 9,9 až 10,1 s. O mnoho užší interval ani nelze zvolit, potřebujeme totiž, aby se při vzorkovací frekvenci 44100 Hz vešlo do daného intervalu potřebných 8192 bodů.)
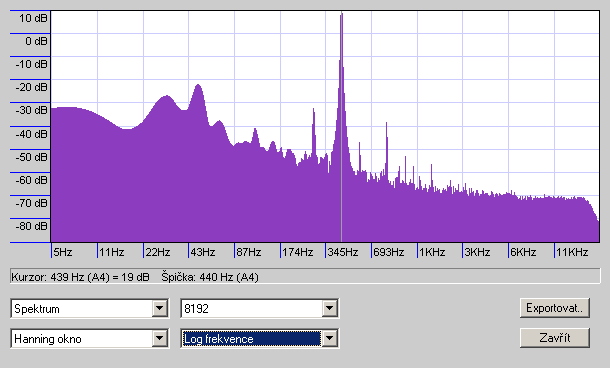
Obr. 3 Spektrum zvuku dovoluje přesněji určit hlasitost zvuku ladičky
Tím ale možnosti analýzy nekončí. Audacity dovoluje spektrum exportovat do textového souboru. Tímto způsobem můžeme určovat hodnoty hlasitosti s přesností na desetiny decibelů i vyšší. (Samozřejmě, hodnotám na mnoho desetinných míst nelze věřit. Navíc, frekvence nejsou v celých Hz. Přece jen, Audacity je program určený pro jiné účely než pro školní fyzikální měření, tak od něj nemůžeme chtít zázraky. Ale s trochou opatrnosti při hodnocení výsledků nám slouží velmi dobře.)
Takto můžeme odečíst hlasitosti v různých časech, výsledky zadat do Excelu a zobrazit do grafu. Obrázek 4 ilustruje, že hlasitost opravdu klesá s časem lineárně – v našem případě o necelé tři čtvrtiny decibelu za sekundu.
Pro ladičku bez skříňky podobná analýza naznačuje, že útlum se v tomto případě s časem poněkud mění – otázky s tím související a možné vysvětlení však bude lépe nechat do samostatného článku.
Energie ladičky – a „krok do nanosvěta“
Položili jste si někdy otázku, jaká je energie kmitů ladičky? Může nás to dovést až k docela překvapivým závěrům.
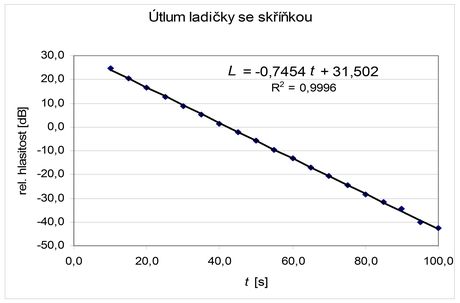
Obr. 4 Útlum ladičky analyzovaný v Excelu
Ladička jako siloměr či váhy? (Odhadujeme tuhost ladičky)
Pro odhad energie nejprve uděláme „úkrok stranou“. Jistěže nechceme z ladičky doopravdy dělat siloměr. Ale přece jen – zkuste stlačit ramena ladičky k sobě. O kolik se pohnula?
Tuhost ladičky lze odhadnout i velmi jednoduchým pokusem. Silou, kterou budeme tlačit na konec ramene ladičky, může být třeba tíha PET láhve s vodou (tedy asi 15 N). Druhé rameno opřeme o stůl. Ti, kdo chtějí být přesnější, mohou k měření posuvu konce ramene užít posuvné měřítko; pro odhad však poslouží i značky na kousku papíru. Já jsem v případě výše uvedené síly odhadl přiblížení konců ramen na několik desetin milimetru, dejme tomu 0,3 mm. Každé rameno se tedy ohnulo o 0,15 mm, což při síle 15 N dá tuhost k = 15/0,00015 N/m = 105 N/m.
Energie kmitů ladičky
Těsně po úderu do ladičky kmitání ramen vidíme pouhým okem. Amplitudu A kmitů ramene tedy můžeme odhadnout na několik desetin milimetru, řekněme A = 0,3 mm. Energii (při maximální výchylce) pak můžeme odhadnout pomocí vztahu 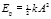 . Energie obou ramen je dvojnásobná, takže
. Energie obou ramen je dvojnásobná, takže
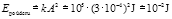 .
.
Ke stejnému výsledku můžeme dospět i z kinetické energie. Maximální rychlost pohybu konce ramene je v = ω·A. Úhlová frekvence je ωv =2πf, tedy 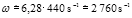 . Maximální rychlost konce ramene je tedy necelý 1 m/s. (Přesněji je ωA asi 0,8 m/s.) Ke kinetické energii ramene nejvíce přispívá pohyb jeho konce (průhyb ramene je složitou funkcí polohy, ale části dále od konce se opravdu pohybují málo). Ladička má hmotnost přes 200 g, výrazně se pohybující kus na konci ramene tedy bude mít hmotnost řekněme 10–15 g. (Zdá se to málo, ale je to kousek o délce asi 2 cm; jak lze odhadnout i z hustoty a objemu.) Kinetická energie
. Maximální rychlost konce ramene je tedy necelý 1 m/s. (Přesněji je ωA asi 0,8 m/s.) Ke kinetické energii ramene nejvíce přispívá pohyb jeho konce (průhyb ramene je složitou funkcí polohy, ale části dále od konce se opravdu pohybují málo). Ladička má hmotnost přes 200 g, výrazně se pohybující kus na konci ramene tedy bude mít hmotnost řekněme 10–15 g. (Zdá se to málo, ale je to kousek o délce asi 2 cm; jak lze odhadnout i z hustoty a objemu.) Kinetická energie 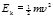 po vynásobení dvěma (abychom dostali energii obou ramen) tedy rovněž vychází zhruba 0,01 J.
po vynásobení dvěma (abychom dostali energii obou ramen) tedy rovněž vychází zhruba 0,01 J.
Souhlas obou odvození pro nás ostatně nemusí být žádným překvapením. Souvisí totiž se vztahem 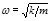 pro frekvenci kmitů. A už hrubý řádový odhad dá pro k = 105 N/m a m = 10–2 kg hodnotu ω2 = 107 s–2, tedy
pro frekvenci kmitů. A už hrubý řádový odhad dá pro k = 105 N/m a m = 10–2 kg hodnotu ω2 = 107 s–2, tedy 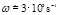 , takže naše řádové odhady „sedí“.
, takže naše řádové odhady „sedí“.
Když už ladičku sotva slyšíme… – aneb ladička a nanometry
Nad setinou joulu se asi nikdo nepozastaví. Pojďme se však podívat, jaká je energie ladičky a odpovídající amplituda kmitů v okamžiku, kdy ladičku právě přestáváme slyšet.
Na obr. 4 vidíme, že počítačem můžeme analyzovat útlum v rozsahu asi 70 dB. V prvních asi 10 s po úderu je hlasitost pro počítač příliš vysoká, velmi slabé signály se zase již „utápějí“ v šumu způsobeném i zvukovou kartou počítače. Uchem však stále ještě můžeme ladičku slyšet. Pokusy v hluboké noci a mimo město (k zajištění co nejtiššího okolí) ukázaly, že od úderu do okamžiku, kdy ladičku přestaneme slyšet, byl pokles hlasitosti až 100 dB. To znamená pokles energie ladičky o faktor 10–10.
Stejný odhad dostaneme i ze vztahu pro hlasitost L = 10·log(I/I0), kde intenzita zvuku při hlasitosti 0 dB je I0 = 10–12 W/m2. Výkon zdroje zvuku tedy musí být 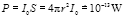 , jestliže za vzdálenost r od zdroje (ladičky) k uchu dosadíme necelých 10 cm. Je-li energie ladičky E = 10–12 J a většina z ní se vyzáří ve formě zvukových vln asi za 10 s (to zhruba odpovídá útlumu ladičky, jaký jsme naměřili), dostáváme právě uvedený výkon 10–13 W. (Vztah mezi výkonem a energií bychom mohli vyjádřit přesněji pomocí derivace energie podle času, ale na úrovni SŠ zřejmě postačí výše uvedená přibližná úvaha.) Opět tedy dostáváme energii o deset řádů nižší než těsně po úderu do ladičky.
, jestliže za vzdálenost r od zdroje (ladičky) k uchu dosadíme necelých 10 cm. Je-li energie ladičky E = 10–12 J a většina z ní se vyzáří ve formě zvukových vln asi za 10 s (to zhruba odpovídá útlumu ladičky, jaký jsme naměřili), dostáváme právě uvedený výkon 10–13 W. (Vztah mezi výkonem a energií bychom mohli vyjádřit přesněji pomocí derivace energie podle času, ale na úrovni SŠ zřejmě postačí výše uvedená přibližná úvaha.) Opět tedy dostáváme energii o deset řádů nižší než těsně po úderu do ladičky.
Jak jsme již připomněli výše, energie je úměrná druhé mocnině amplitudy A. Pokles energie o deset řádů tedy odpovídá poklesu amplitudy o pět řádů. Amplituda kmitů ramen ladičky v okamžiku, kdy ji přestáváme slyšet, je tedy řádově
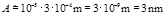 .
.
Naše úvahy jsou samozřejmě přibližné a pouze řádové. (Nebrali jsme v úvahu různou citlivost ucha pro různé frekvence, směrovou charakteristiku vyzařování ladičky a další faktory.) Ale právě ten řád výsledku je překvapující:
Ve chvílích, kdy ladičku (v naprosto tichém prostředí) přestáváme slyšet, kmitají její ramena s amplitudou jen řádu nanometrů! Může to působit zvláštně, ale rozměry, které hrají roli v dnes tak populárních nanotechnologiích, můžeme tedy ilustrovat na kmitech obyčejné ladičky… Současně nám to možná pomůže udělat si bližší představu o citlivosti (a o rozsahu citlivosti) našeho sluchu. Představu, kterou si pod běžně uváděnou „mezní“ intenzitou I0 = 10-12 W/m2 asi málokdo běžně uděláme.
Pokud by vám připadaly nanometry ještě stále moc velké, pak se můžeme zeptat, s jakou amplitudou kmitá držák ladičky. (Právě jeho kmity převádějí kmitání do rezonanční skříňky.) V článku [2] uvádějí autoři výsledky měření, z nichž plyne, že amplituda kmitů držáku je asi 300-krát menší než amplituda konce ramene. To znamená, že v okamžiku, kdy ladičku přestáváme slyšet, je amplituda kmitů držáku řádu 10–11 m, tedy zhruba desetkrát menší, než jsou rozměry atomů. Zdá se to neuvěřitelné? Ale ano, makroskopické těleso může kmitat s takto malou amplitudou. Jde o vystředovaný pohyb všech částic, které samy mohou kmitat s větším rozkmitem. Podobně je tomu u detektorů gravitačních vln – detektor LIGO má mít konečnou citlivost takovou, že bude detekovat pohyby několik kilometrů vzdálených zrcadel s amplitudou 10–18 m (viz [10]), tedy tisíckrát menší než je velikost atomového jádra. Kam se na to hrabeme s naší ladičkou! Ale stejně je zajímavé, do jakých rozměrů a k jakým analogiím nás „obyčejná školní ladička“ přivedla.
Závěr
O ladičce jsme zdaleka neřekli vše a určitě jsme nevyčerpali ani všechna její zajímavá využití ve výuce fyziky. Nevěnovali jsme se ladičkám jiných frekvencí než 440 Hz, ladičce s připevněným hrotem, jímž můžeme kreslit stopu kmitů na začazené sklo, vlnám, které vzniknou na vodě, když se ladičkou dotkneme její hladiny, možnosti demonstrovat přenos zvuku pevnými látkami… Snad ale alespoň některé z popsaných pokusů, měření a úvah mohou inspirovat vás, učitele fyziky, ať už k demonstračním experimentům, laboratorním pracím či malým projektům pro žáky a studenty. Ladička nám v nich může být opravdu dobrou pomůckou.
Literatura
[1] Lepil O.: Fyzika pro gymnázia. Mechanické kmitání a vlnění. Prometheus, Praha 1994
[2] Rossing T. D., Russel D. A., Brown D. E.: On the acoustics of tuning force. Am. J. Phys. 60 (1992), 620-626
[3] Russel D. A.: On the sound field radiated by a tuning fork. Am. J. Phys. 68 (2000), 1139-1145
[4] Kraftmakher Y.: Computerized experiments with a tuning fork. Eur. J. Phys. 25 (2004), 869-875
[5] Zeitnitz Ch.: Soundcard Oscilloscope. [online] http://www.zeitnitz.de/Christian/Scope/Scope_en.html [cit. 5. 9. 2006]
[6] Veletrh nápadů pro fyzikální vzdělávání. CD – elektronický „superborník“ příspěvků z prvních devíti ročníků konference Veletrh nápadů učitelů fyziky. Ed. L. Dvořák, Z. Broklová, Prometheus, Praha 2005
[7] Koudelková I.: ústní sdělení. (Tím chci říci, že daný problém znám od I. Koudelkové. Tu s ním seznámil jeden z původních zakladatelů projektu Heuréka B. Bílý. Není vyloučeno, že jde o problém popsaný ve starší literatuře, v současnosti však zřejmě není příliš znám.)
[8] Audacity [online] http://audacity.sourceforge.net/ [cit. 6. 9. 2006]
[9] Dvořák L.: Pokusy se zvukovou kartou. In: Dílny Heuréky 2005. Sborník konference projektu Heuréka, Náchod, září 2005. Ed. L. Dvořák. Prometheus, Praha 2006
[10] CIT LIGO Laboratory, MIT LIGO Laboratory: LIGO Vocabulary [online] http://www.ligo.caltech.edu/~ll_news/0607a_news/LIGO_Vocabulary.htm [cit. 5. 9. 2006]
