Optické experimenty s data-projektorom
Ivan Baník
Dataprojektor je moderný projekčný prístroj, ktorý sa čím ďalej tým viac uplatňuje nielen vo výučbe v školských podmienkach, ale aj v prezentačnej činnosti rôznych firiem a inštitúcií, pri príležitosti rôznych školení, seminárov i v reklamnej činnosti. V školských podmienkach sa v rámci výučby fyziky dajú uplatniť okrem jeho bežných projekčných možností a schopností aj jeho menej známe vlastnosti – jeho „talent“ pre živé optické experimenty a demonštrácie v rámci učiva z geometrickej i vlnovej optiky. Umožňuje to predovšetkým fakt, že dataprojektor je zdrojom intenzívneho svetelného žiarenia, ale aj to, že jeho žiarivý tok možn„ vhodne modifikovať prostredníctvom počítača. V ďalšom uvedieme niekoľko konkrétnych možností uplatnenia dataprojektora vo výučbe optiky.
Čo treba urobiť pred pokusom
Pred vlastným optickým pokusom vytvoríme na počítači (napr. aj priamo v power-pointe) rozmernejší obrazec vodorovnej, alebo zvislej bielej štrbiny na čiernom podklade (obr. 1). Štrbina je umiestnená viac-menej v strednej časti obrazovky. Na projekčnej ploche sa po zaostrení dataprojektora objaví „svietiaca“ štrbina na tmavom neosvetlenom okolí.

Obr. 1
Spektrum vytvorené pomocou hranola
Usporiadanie pokusu je na obr. 2. Aj pri tomto pokuse zobrazíme na projekčnej ploche najprv svietiacu – v tomto prípade vodorovnú – štrbinu. Hranol, otočený lámavou hranou smerom nadol, umiestníme tesne pred projektor. Spektrum sa pozoruje buď na povale-plafóne, alebo na papieri, vhodne postavenom do cesty lúčom. Pri využití zvisle postavenej svietiacej štrbiny musí byť lámavá hrana hranola tiež zvislá.
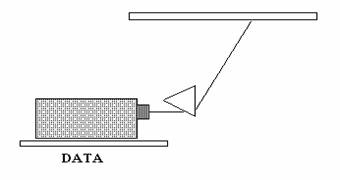
Obr. 2
Interferenčné pokusy s dataprojektorom a CD platňou
Pri týchto pokusoch sa využíva interferencia svetla na odraznej CD-mriežke. Pokus je znázornený na obr. 3. Vykonáme ho tak, že tesne pred projektor umiestnime zvislú bielu rovinnú pracovnú plochu – lúčovú rovinu LR, ktorá je takmer rovnobežná s lúčmi vystupujúcimi z projektora. Pri správnom nastavení jej polohy dosiahneme stav, pri ktorom sa na nej objaví relatívne úzky a intenzívny lúč vychádzajúci z projektora. Ak tomuto lúču postavíme do cesty vhodne umiestnenú CD platňu tak, ako to ukazuje obr. 3, môžeme na doske pozorovať viaceré difragované lúče, zodpovedajúce jednotlivým interferenčným maximám. Všetky difragované lúče, okrem zväzku prislúchajúceho nultému maximu vykazujú aj určité spektrálne sfarbenie, nakoľko ide o zložené, nemonochromatické svetelné žiarenie projektora.
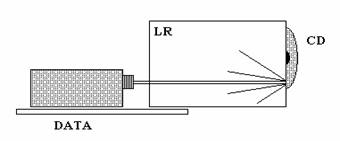
Obr. 3
Príslušné „difrakčné“ uhly αi zodpovedajúce jednotlivým maximám príslušnej farebnej zložky (pri kolmom dopade svetla) môžeme zmerať (od kolmice dopadu), alebo aspoň odhadnúť a na základe toho vypočítať vlnovú dĺžku svetla pre jednotlivé farebné zložky. Z nameraného uhla αi pre i-te maximum určíme vlnovú dĺžku na základe vzťahu
![]()
kde O1O2 = 1,6 μm (mikrometra) je príslušná mriežkova konštanta CD mriežky, ktorú vypočítame zo známej hustoty záznamových stôp CD platne rovnej 625 stôp na milimeter.
Ak zmeriame uhol α1 prislúchajúci prvému maximu i = 1, bude pre vlnovú dĺžku platiť
![]()
Pri zmene sklonu CD-platne sa mení aj interferenčný zväzok.
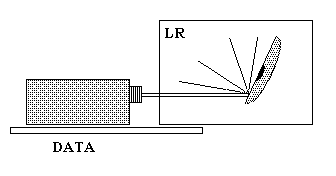
Obr. 4
Pre pozorovanie tohto efektu je však vhodnejšie usporiadanie znázornené na obr. 4, pri ktorom sa využíva iba polovica CD platne tvaru polkruhu, ktorú získame rozstrihnutím CD-platne pomocou trochu masívnejších nožníc. Takýto CD-polkruh môžeme potom umiestniť na ľubovoľné miesto lúčovej roviny LR, ktorým prechádza svetelný lúč. Pri natáčaní CD-polkruhu môžeme pozorovať difragované lúče pri rôznych uhloch β dopadu lúča na odraznú CD-mriežku. Príslušné uhly αi prislúchajúce jednotlivým interferenčným maximám môžeme zmerať a na základe toho vypočítať vlnovú dĺžku svetla pre jednotlivé farebné zložky. Pre vlnovú dĺžku platí vzťah
![]()
kde β je uhol dopadu. Horné znamienko platí, ak difragovaný lúč leží na opačnej strane od kolmice dopadu, ako lúč dopadajúci. Ak odrazený lúč – zodpovedajúci nultému maximu – usmerníme do smeru kolmého na dopadajúci lúč, bude uhol dopadu rovný 45 stupňov.
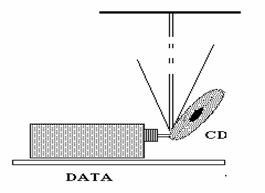
Obr. 5
Pokus s CD-spektrom na plafóne
Pri tomto pokuse (Obr. 5) sa zaobídeme bez lúčovej roviny. CD platňu postavíme tesne pred projektor v sklonenej polohe so sklonom asi 45 stupňov tak, aby svetlo z projektora dopadalo na ňu v jej najnižších častiach. Interferenčné spektrum prvého rádu pozorujeme na povale-plafóne v miestach nad projektorom.
Interferencia svetla na transparentnej optickej mriežke
Pri tomto pokuse vychádzame zo situácie, keď je na projekčnej ploche na začiatku ostro zobrazená relatívne úzka, v tomto prípade zvislá svietiaca štrbina. Ak v takomto stave postavíme tesne pred objektív dataprojektora transparentnú optickú mriežku s ryskami rovnobežnými so štrbinou (Obr. 6), na projekčnej ploche sa vytvorí interferenčný obrazec. Pozorujeme na ňom niekoľko interferenčných maxím a miním. Hustota maxím a miním závisí, pochopiteľne, od mriežkovej konštanty mriežky. Vhodné sú mriežky už aj s desiatkou čiar na jeden milimeter.
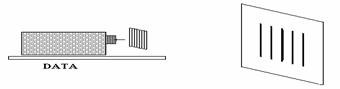
Obr. 6
Pri určení strednej hodnoty vlnovej dĺžky svetla vychádzame v prípade optickej mriežky neveľkej hustoty z obvyklého vzťahu
![]() ,
,
kde O1O2 je príslušná mriežkova konštanta, y je vzdialenosť susedných interferenčných maxím na projekčnej ploche a d je vzdialenosť od mriežky k projekčnej ploche.
Ak ide o mriežky so značne vyššou hustotou, interferenčný obrazec možno lepšie pozorovať na bielom tienidle umiestnenom bližšie k projektoru. V takých situáciach - kedy ide o väčšie difrakčné uhly - treba pri výpočte vlnovej dĺžky použiť vzťah (1, resp. 2).
Interferencia svetla na gramo-platni
Pri tomto pokuse (obr. 7), dopadá svetlo na gramoplatňu pod veľkým uhlom dopadu – blízkym 90 stupňov. Difrakčné spektrum pozorujeme na stene, resp. projekčnej ploche umiestnenej – ako obvykle – vo väčšej vzdialenosti od projektora. Pri zmene sklonu gramoplatne sa pozorované spektrum premiestňuje, pričom sa mení aj jeho šírka.
V zásade môžeme gramoplatňu postaviť aj do šikmejšej polohy, pri ktorej sa príslušné spektrum zobrazí na plafóne. V tejto situácii je však spektrum relatívne úzke a menej výrazné. Výraznejšie je len pri väčšej výškovej dimenzii miestnosti.

Obr. 7
Poznámka: Dataprojektor možno využiť aj pri viacerých lúčových pokusoch z geometrickej optiky. Do tejto skupiny pokusov patria pokusy, pri ktorých sa demonštruje zákon odrazu, lomu, posunutie lúčov pri prechode planparalelnou doskou a pod. V niektorých prípadoch je vhodné na počítači vytvoriť sústavu viacerých navzájom rovnobežných štrbín, čo umožní získať na lúčovej rovine LR (ktorou môže byť aj stena) sústavu navzájom rovnobežných lúčov. Tie necháme potom dopadať na zrkadlo, lámavú plochu a pod.
Záver
V článku je poukázané na to, že dataprojektor môže mať vo výučbe fyziky aj určité špecifiké možnosti uplatnenia. Je to prístroj vhodný aj na živé optické demonštračné experimenty či už v rámci výučby geometrickej, alebo vlnovej optiky.
Literatúra
[1] I. Baník, R. Baník: Meranie vlnovej dĺžky svetla pomocou CD platne, MFI 5, 1996, s. 26-29
