Panská fyzika ze Štupky
Jaroslav Reichl, Vítězslav Jíra
Na úvod malé vysvětlení nadpisu – to není vychloubání, to má být pouze pokus o vtip. Naše škola má v Praze k dispozici dvě budovy – jednu v Panské ulici a druhou v Malé Štupartské a právě ve „Štupce“ je učebna fyziky, fyzikální kabinet a sídlo přírodních věd vůbec. Proto ten netradiční název příspěvku. Navíc v době, kdy bylo třeba poslat přihlášku s názvem vystoupení, jsem nevěděl, s čím „ponesu kůži na trh“, takže tímto způsobem jsem si nechával otevřená „zadní vrátka“. Ale teď již k fyzice samotné.
Dávám k dispozici několik námětů na pokusy, resp. na oživení výuky fyziky na střední škole. Některé jsou z mé hlavy, některé jsem „okoukal“ jinde a mírně modifikoval, ale tím se netajím.
Sluneční soustava
V prvním ročníku se v kapitole věnované gravitačnímu poli v okolí hmotných bodů zavádí v souvislosti se sluneční soustavou a Keplerovými zákony veličina v astronomii často používaná – astronomická jednotka. Studenti se dozví, jak se definuje, proč se zavádí, jaká je její velikost. A počítají se úlohy. Sám jsem se poněkud více zajímal o astronomii, takže mám vždy co dělat, abych se držel osnov a nezačal vykládat podrobně o sluneční soustavě, jednotlivých planetách, kometách, … více, než mi dovoluje čas. Přesto se rozpovídám malinko více a tudíž dojde na vzdálenosti jednotlivých planet od Slunce. A tady je kámen úrazu. Přiznám se, že teprve po sestavení následujícího modelu člověku dojde, jak „prázdná“ sluneční soustava vlastně je.
K sestavení jednoduchého modelu sluneční soustavy je třeba: pevný provázek (alespoň 4,5 m dlouhý), kreslicí čtvrtka či jiný tužší papír, kružítko, nůžky, tužka, 2 stativy (buď školní nebo z PET lahví). Z papíru jsem vystřihl 10 koleček (9 planet a Slunce) s poloměrem 2 cm. V jejich středu jsem udělal dírku na provlečení provázku. Poblíž jednoho konce provázku (necháme kousek na přivázání ke stativu) připevníme Slunce. A nyní v poměru 1 AU = 10 cm umisťujeme na provázek další planety, jejichž vzdálenosti lze nalézt v Matematicko-fyzikálních tabulkách. Já osobně jsem si pro případ zvídavých dotazů studentů na kolečka reprezentující jednotlivé planety z tabulek vypsal vzdálenost od Slunce, dobu oběhu kolem Slunce (periodu), rovníkový průměr planety a poměr hmotnosti planety vzhledem k hmotnosti Země a astronomickou značku planety. A jednoduchý model sluneční soustavy, na kterém je názorně vidět rozložení planet kolem Slunce, je hotov.
Planety sluneční soustavy
Máme-li k dispozici model sluneční soustavy, na němž jsou vidět vzdálenosti jednotlivých planet od Slunce, chtělo by to ještě nějak ukázat vzájemnou velikost (srovnání) jednotlivých planet. V nejrůznější literatuře se člověk dočte různá přirovnání (míče, špendlíkové hlavičky, kuličky hrachu, …), což sice může pomoci, ale problém je uvažované modely sehnat a mluvit o nich „zpaměti naslepo“, to není ono. Proto jsem si vypomohl opět s pomocí několika čtvrtek, kružítka, barevných pastelek, vodovek a nůžek a vytvořil modely rovinné.
Před vlastní výrobou pomůcky bylo třeba vymyslet správný poměr pro zmenšení skutečného průměru planety tak, aby bylo možno rozumně sestrojit model jak např. Pluta, tak i Jupitera. Rozhodl jsem se pro poměr 1: 200 000 000. Mnou použité hodnoty jsou v následující tabulce:
Planeta |
Průměr planety |
Průměr modelu |
Planeta |
Průměr planety |
Průměr modelu |
Merkur |
4878 km |
2,44 cm |
Saturn |
120536 km |
60,27 cm |
Venuše |
12102 km |
6,05 cm |
Uran |
51118 km |
25,56 cm |
Země |
12756 km |
6,40 cm |
Neptun |
49528 km |
24,76 cm |
Mars |
6794 km |
3,40 cm |
Pluto |
2360 km |
1,18 cm |
Jupiter |
142984 km |
71,49 cm |
Měsíc |
3476 km |
1,74 cm |
Nyní již stačí s pomocí kružítka a nůžek sestrojit příslušné modely a obarvit je. Barvy jednotlivých modelů jsem hledal v kapesním průvodci Planety naší sluneční soustavy a na Internetu.
Sluneční soustava na počítači
Do třetice všeho dobrého, a tak tu máme třetí setkání se sluneční soustavou. Tentokráte v počítačové podobě od studenta prvního ročníku naší školy – Vítězslava Jíry. Ten v programu „3D Studio“ vytvořil pohyblivé animace planet sluneční soustavy (viz obrázky). Ke spuštění těchto animací není nutný zmíněný program – stačí systém Windows s instalací přehrávače souborů s příponou AVI (videoklipů).
Do budoucna Vítek plánuje zobrazení všech planet najednou včetně „zabudování“ Keplerových zákonů, tj. planety se poté budou po svých trajektoriích pohybovat nerovnoměrně právě podle Keplerových zákonů. Zatím jsme si jen tak hráli a seznamovali se s prostředím „3D Studia“. Víme totiž, že „kdo si hraje, nezlobí …“
Kinetická energie rotujícího tělesa
Při výkladu mechanické energie studenti většinou snadno pochopí, jak se projeví u hmotného bodu jeho kinetická energie posuvného pohybu a potenciální energie. Kinetická energie rotujícího tuhého tělesa už je ale na představu a pochopení těžší. Není tedy nic jednoduššího než přesvědčit studenty, že rotující tuhé těleso tuto energii skutečně má. Vyrobil jsem tedy model setrvačníku. Vymontovat z FAVORITA přední kolo není problém, ale kolo je lehké a tudíž má malý moment setrvačnosti. K jeho zvýšení bylo zapotřebí zvětšit hmotnost na obvodu kola. Vylévat ráfek olovem, jak předvádějí vyučující na MFF UK, jsem zavrhl. Hledal jsem tedy jednodušší způsob.
Ke zhotovení následující pomůcky je třeba přední kolo z jízdního kola (FAVORIT) bez pneumatiky a duše, 18 lahviček od Actimelu, suchý písek, izolepa, gumičky, igelitové sáčky (nebo fólie na potraviny). Lahvičku do Actimelu naplníme pískem a pomocí igelitu a gumičky ji uzavřeme. Poté ji položíme do ráfku kola a několikrát obmotáme izolepou. Analogicky postupujeme s dalšími lahvičkami. Před začátkem lepení lahviček je třeba alespoň zhruba vyměřit vzdálenosti mezi lahvičkami, aby se kolo otáčelo rovnoměrně.
Nyní kolo uchopíme za „motýlky“ tak, aby jeho osa byla vodorovná, a roztočíme (buď požádáme někoho, nebo zvládneme sami) a setrvačník je na světě. Půjčíme-li tento setrvačník do ruky studentům, roztočíme jej a poté je vyzveme, aby zkusili rotující kolo natočit (tj. změnit vodorovnou polohu osy kola), zjistí, že to není tak jednoduché. Zopakuje-li si student popsaný experiment s různými úhlovými rychlostmi otáčení kola, může si ověřit, že s rostoucí úhlovou rychlostí roste i kinetická energie rotujícího tělesa (závislost na druhé mocnině této úhlové rychlosti ukázat nelze).
Se zvídavějšími studenty můžeme zavést řeč i na piruety krasobruslařů, vznik rotace planet při vzniku sluneční soustavy, … a nastínit veličinu zvanou moment hybnosti a zákon jeho zachování. K tomu lze využít otáčející se židli, na níž se posadí sám učitel nebo student, a postupným nakláněním osy kola vyvolat rotaci celé židle. Přestože nemám speciálně vyrobenou židli jako na MFF UK, podařilo se mi celkem slušně se otáčet.
Během práce s roztočeným setrvačníkem je třeba dávat pozor, aby nedošlo ke zranění. Zvláštní pozornost je třeba věnovat při brždění kola. Věřte, docela to bolí.
Přilepení plecháčku ke sklu bez lepidla
K tomuto pokusu z termodynamiky, konkrétně z oblasti skupenských přeměn, je třeba: klasický plecháček, podložní sklo, na které se plecháček vejde, kus polystyrenu (jako tepelná izolace), drcený led, voda a sůl.
Na skleněnou destičku, kterou tepelně izolujeme vhodným podkladem (např. polystyren), nakapeme trochu vody. Poté na ní položíme plecháček s jemně roztlučeným ledem a na led nasypeme trochu kuchyňské soli. Nyní necháme několik minut stát. Poté, chceme-li zvednout plecháček vzhůru, pozorujeme, že je k němu přimrzlá skleněná destička.
A vysvětlení? K tání ledu je třeba dodat soustavě skupenské teplo tání. Toto teplo je zde dodáváno samotnou směsí (reakce soli s ledem). Proto se směs ochlazuje, což vyvolává zamrzání vody mezi plecháčkem a skleněnou destičkou.
Při pokusu je třeba dbát na to, aby do vody pod plecháček nenapadaly krystalky soli.
Tento pokus není z mé hlavy, ale našel jsem ho v knize „Fyzikální kvízy“ od B. F. Bilimoviče.
Další spojení na mě, resp. autora animací, je možné pomocí e-mailu: reichl@panska.cz.
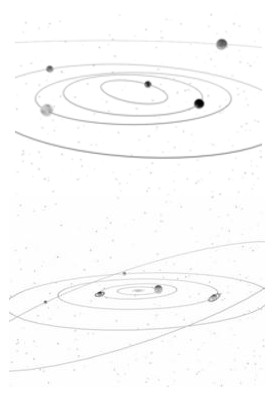
Obr. 1

Obr. 2: Země

Obr. 3: Mars

Obr. 4: Saturn
