Trocha heuristiky z Malé Hraštice

Leoš Dvořák

Malá Hraštice je vesnička poblíž Dobříše, proslavená skutečně vynikající pekárnou a cukrárnou – a pro znalce též turistickou základnou, ideální pro pořádání nejrůznějších akcí v poněkud „polních podmínkách“. Na pár květnových dní letos ožila i fyzikou.

Možnost vskutku nespoutaně experimentovat zde už od roku 1997 využívá skupina studentů učitelství fyziky MFF UK, několika jejich učitelů a spřízněných duší, tvořících vágně definovanou Společnost pro obnovu Hraštických tabulek.

(Pozn.: Termín Hraštické tabulky pronikl už i na mezinárodní konferenci [1]. Což teprve až budou skutečně existovat…)

Oč jde na Hraštici

Zmíněná několikadenní soustředění s posluchači studia učitelství fyziky jsou velice užitečnou formou, jak prohloubit kontakt s posluchači, zahrát si hry nevážné i psychologicky laděné atd. Fyzika přitom vůbec není v pozadí, naopak. Možnost provádět pokusy s jednoduchými pomůckami, vymýšlet vlastní varianty pokusů, využívat netradiční materiály, vytvářet vlastní pomůcky a přístroje – to vše je nesmírně atraktivní pro všechny zúčastněné. Na fyziku známou z učebnic, přednášek i praktik se otvírá další pohled. A nejen pohled. Heslem našich táborů je totiž vlastníma rukama a hlavou.

Účastníci tak pro sebe leccos z fyziky objevují. Někdy znovu, někdy – například jde-li o propojení „vysokoškolské“ a „elementární“ fyziky – možná i poprvé. Zároveň se nenásilně seznamují s heuristickou metodou výuky. S tím, že experimentovat a objevovat je cennější, než být poučován. Věříme, že tyto zkušenosti v budoucnu uplatní ve své profesi.

Hlavním tématem letos byla právě tvorba jednoduchých fyzikálních přístrojů a zařízení. Náměty byly zadány velmi obecně: Zkonstruujte přístroj na měření libovolné veličiny dle vlastního výběru (délky, času, rychlosti, hmotnosti, koeficientu tření, …) nebo jakékoli technické zařízení využívající fyzikálních principů (telefon, elektrárnu, balón, ponorku, …). Vynalézavosti se meze nekladou. To vše skutečně „na koleně“; z drátů, hřebíků, prkének, špejlí. Nejsložitějším nástrojem byla ruční elektrická vrtačka.

Všehochuť nápadů

Z vytvořených konstrukcí lze zmínit hodiny (sluneční, svíčkové i přesýpací) nebo siloměry využité i k měření (resp. odhadu) viskozity medu. Táhnout siloměrem krajíc chleba po pekáči pomazaném medem poskytne vskutku nezapomenutelnou podívanou. Nejnáročnější konstrukcí byla elektrárna na blízkém potoce. Vodní kolo přes převod pohánělo alternátor, tvořený cívkami navinutými na plastikové láhvi od kakaa, v níž se otáčel magnet. Převod gumičkou sice vydržel vždy jen chvíli, ale „elektrárna“ přesto dokázala rozsvítit diodu LED. Nyní již podrobněji k některým dalším nápadům.

Nitkový telefon s ozvěnou

Telefon z kelímků, jejichž dna jsou spojena napnutou nití, si v dětství udělal snad každý z nás. Leckdo možná vytvořil i telefon vedoucí za roh, nebo telefon s více účastníky, k nimž nitě vedou hvězdicovitě od společného středu.

Na Hraštici posluchači z prvního ročníku, vedeni snahou mít více účastníků, udělali „hlavní vedení“ tvořené nití dlouhou asi 30 m napnutou mezi dvěma stromy. Na tuto nit se prakticky kolmo napojovaly nitě vedoucí ke kelímkům. Napojovat nitě kolmo se asi nejeví jako nejlepší nápad a zřejmě to snižuje účinnost celého zařízení. V nitkovém telefonu se totiž zvuk přenáší podélným vlněním. Díky svému uspořádání ale daná konstrukce vykázala překvapivý efekt.

V „hlavním vedení“ se totiž na koncích vlnění odráželo. Po krátkém hlasitém zavolání do kelímku bylo možno slyšet ještě asi 3 až 4 ozvěny!

I na notoricky známém nitkovém telefonu tak lze nalézt něco nového. Navíc se zde nabízejí náměty na zkoumání spousty zajímavé fyziky: Jak je to s rychlostí šíření zvukových vln v napnuté niti? Jak je to s odrazem na koncích a jak v místě spojení dvou nití? Jak se vlnění odráží a jak tlumí na membráně tvořené dnem kelímku? Jakou tuhost má mít membrána, aby byla účinnost nitkového telefonu co nejlepší? Zde bychom se asi dostali k pojmům jako impedance, přizpůsobení a ke skutečným elektroakustickým zařízením. Na nitkovém telefonu se zjevně lze „vyřádit“ na mnoha úrovních, od té nejhravější až po vysokoškolskou.

Archimedovské váhy

Opět originální konstrukce posluchačů prvního ročníku. Funkce je zřejmá z obrázku: Plastová láhev od kakaa zatížená uvnitř pískem plave ve vědru s vodou. Od ní vede provaz přes kladku. Na druhý konec provazu se věší vážený předmět. Na vnější stěně láhve od kakaa (je krásně žlutá a dobře se na ni píše fixem) je nakreslena stupnice. Ryskou je hladina vody.

Jednoduché a účelné zařízení, které by šlo upravit pro vážení předmětů od 10 dekagramů salámu (pro výrazně lehčí předměty by mohly vadit kapilární síly) až třeba po samotného pedagoga (jen by to chtělo větší vědro, láhev a pevnější kladku).

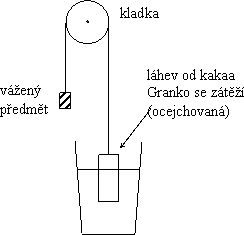
Je dobře uvědomit si, že v daném uspořádání nezáleží na množství vody ve vědru ani na tom, že stěny vědra jsou šikmé. Inu – Archimédův zákon v praxi.

Měření pružnosti džemu

O Youngově modulu pružnosti látek se mluví na střední škole i v úvodním vysokoškolském kurzu fyziky. Většinou ale s odkazem na pružnost materiálů jako je ocel. Tomu odpovídají i případné pokusy: natahování tenkých drátků. Co ale zkusit změřit pružnost „méně tradičních“ materiálů? Třeba džemu, který si mažeme na chleba nebo na vánočku k snídani?

Takový džem lze stlačit snáze než ocel. Lze tedy stlačovat kvádřík o stranách dlouhých cca 1 až 2 cm a i při dosti malých silách dosáhnout pozorovatelné deformace.

Přístroj pro měření Youngova modulu pružnosti džemu a podobných materiálů může být velmi jednoduchý. Základem je dvojzvratná páka. Vhodným materiálem se ukázala obyčejná šestihranná dřevěná tužka (je dostatečně tuhá, takže se neohýbá). Uprostřed ji napříč provrtáme vrtáčkem o průměru 1 mm. (V našem případě vrtačkou na plošné spoje, asi by to šlo i běžnou vrtačkou.) Dírou prochází osička, jíž je prostě zavírací špendlík. Drát špendlíku za dírou ohneme; uštípnutím „ouška“ špendlíku (na což stačí běžné kleště „kombinačky“) získáme druhý ostrý konec. Oba pomocí kleští zapíchneme do prkénka, které bude tvořit základnu přístroje, a páka je hotová. Poblíž konce tužky na straně k prkénku přilepíme vteřinovým lepidlem kousek tenké destičky, například umakartu. Destička bude stlačovat kvádřík džemu. K tužce připevníme ještě dvě špejle – na tu u destičky budeme nasazovat matičky jako závaží, které bude stlačovat džem, delší špejle na druhé straně bude sloužit jako ručička. A vše je hotovo.

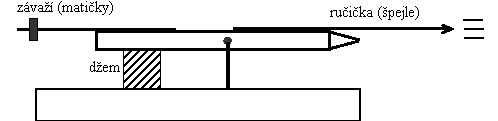
Spočítat z rozměrů přístroje a hmotnosti matiček (na jejich zvážení si případně můžeme vyrobit zvláštní vážky) tlak v džemu a naměřit příslušnou deformaci už je hračkou. Můžeme měřit i pružnost dalších „kuchyňských“ materiálů. Na Hraštici jsem vyzkoušel též knedlík, buřt a „pochoutku“ žužu. Džem má ovšem jednu výhodu. Na hladkou destičku přilne, takže můžeme měřit i jeho pružnost v tahu.

Kontrolovat naměřené hodnoty porovnáním s tabulkovými je problém. Středoškolské matematicko-fyzikální tabulky hodnoty modulu pružnosti tak důležitých materiálů jako džem nebo knedlík prostě neuvádějí. (Už víte, k čemu budou Hraštické tabulky?) Pro zvídavé tedy jen změřený výsledek: U všech výše zmíněných materiálů vyšly hodnoty modulu pružnosti E velmi podobné – řádově milionkrát nižší než tabulková hodnota modulu pružnosti dřeva.

Zesilovač pro snímání kyvů magnetu

Následující konstrukce vznikla díky úloze vyrobit časový normál, tedy zařízení „tikající“ v pravidelných intervalech. Takovým normálem může být kyvadlo. Jak ale nejjednodušeji registrovat například jeho průchod rovnovážnou polohou?

Je-li kyvadlem magnet zavěšený na niti, můžeme průchod snímat indukčně. Pod místo, kde magnet prochází rovnovážnou polohou, umístíme cívku. Pohybující se magnet v ní vyvolá proměnný magnetický tok a na cívce se indukuje napětí. Připojíme-li k cívce měřicí přístroj, při každém kyvu ukáže výchylku.

Jenže: citlivý ručkový měřicí přístroj není to, co chceme při jednoduchých pokusech používat. Malé digitální multimetry zase většinou nestačí na krátký puls napětí zareagovat. Chtělo by to průchod rovnovážnou polohou nějak „zviditelnit“ – například bliknutím svítivé diody.

Svítivá dioda (LED) ovšem vyžaduje napětí minimálně asi 1,6 V. V cívce se indukuje napětí podstatně nižší. Potřebujeme ho tedy zesílit.

Jednu možnost, jak to udělat, ukazuje schéma. Na přesných hodnotách součástek nezáleží; téměř všechny odpory mají jen ochrannou funkci (aby se při vytočení potenciometru k hornímu konci nezničily polovodičové součástky velkým proudem). Tranzistory NPN i PNP mohou být i nejlevnější malé typy, potenciometr stačí libovolný z výprodeje s hodnotou asi 5 až 50 kΩ. Zařízení lze napájet z ploché baterie, která je v celém zapojení nejdražší součástkou.

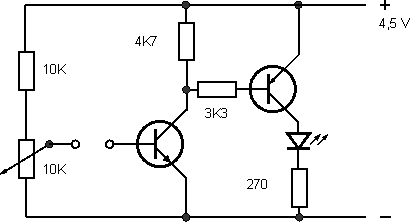
Mezi svorky označené ve schématu připojíme výše zmíněnou cívku, např. 50 závitů drátu na kostřičce asi 5 x 5 cm. (Pro počáteční pokusy o „oživení“ zesilovače můžeme tyto svorky zpočátku spojit drátem.)

Je-li jezdec potenciometru u konce spojeného se záporným pólem baterie, je tranzistor NPN zavřený, neprotéká jím tedy žádný proud do druhého tranzistoru. Ten je proto také zavřený a dioda LED nesvítí. Otáčíme-li potenciometrem, až se napětí na bázi prvního tranzistoru zvýší na asi 0,7 V, začne se tranzistor „otevírat“, pouští proud do druhého tranzistoru, ten jej zesílí a dioda svítí.

Pro naše účely nastavíme potenciometr tak, aby dioda právě začínala svítit. I malé změny napětí, dané napětím indukovaným v cívce, pak budou zesíleny a způsobí výrazné zvýšení jasu svítivé diody. Při opačné polaritě indukovaného napětí se jas naopak sníží.

Kýve-li se teď magnet nad cívkou, při každém průchodu rovnovážnou polohou dioda jasněji blikne. Pozornější pohled ukáže, že kromě zjasnění je zde i moment, kdy jas naopak pohasne – samozřejmě, neboť indukční tok cívkou nejprve roste a pak klesá, takže se postupně indukuje napětí obou polarit.

Celé zařízení může samozřejmě sloužit i jiným účelům než jen ke snímání kyvů magnetu. S dostatečně silným magnetem lze s jeho pomocí demonstrovat vznik indukovaného napětí v cívce doslova o pár závitech. Jak už bylo řečeno, hodí se i v situacích, kdy vzniklé pulsy napětí jsou příliš krátké, než aby je spolehlivě ukázal klasický měřicí přístroj.

Literatura

[1] Dvořák L.: On the Road to Hrastice Tables (Non-traditional Elements in Pre-Service Training of Physics Teachers). In: Sborník z konference Science and Technology Education in New Millenium, Prague, June 15–18. 2000, Ed. R. Šulcová. ISBN 80-86360-14-8. s. 238–242