Pár věcí z tábora 3 – tentokrát o čase a taky trochu o elektronice
Leoš Dvořák
Informace o letním matematicko-fyzikálním táboře pro středoškoláky již zazněla na minulých ročnících Veletrhu nápadů (viz [1]) a tak na tomto místě již není nutno opakovat, komu všemu vděčí za svou existenci. Kromě tradičního kádru organizátorů se však sluší poděkovat několika novým lidem: Lukáši Poulovi, Mgr. Tomáši Ledvinkovi, CSc. a zejména Mgr. Peteru Žilavému. Všichni významně přispěli ke zdaru odborného programu.
Čas a nejen on
Letos jsme byli v lesích u Račic nad Berounkou a hlavním tématem tábora byl čas – což znamená i různá kmitání, pohyby, chaotické děje, čítače atd.
Hlavní formou, kterou se účastníci dozvídali něco nového o fyzice, byly samostatné projekty, na nichž pracovaly dvojice a trojice účastníků. K dispozici byla knihovnička odborné literatury a samozřejmě rada i pomoc konzultantů z řad pracovníků a studentů MFF. Kromě toho běžel i kurs diferenciálního počtu a dostalo se i na přednášky o čase z hlediska astronomie, fyziky mikrosvěta, teorie relativity apod. Došlo i na interdisciplinární témata. Velice zajímavou večerní přednášku o chronobiologii, tj. o časových rytmech živých organismů, nám například udělala Doc. Helena Illnerová, DrSc. z Fyziologického ústavu AVČR. Nejvíce jsme se však chtěli naučit právě na projektech.
Možná trochu překvapivě si z bohaté nabídky témat řada účastníků vybrala věci související s elektronikou. Přesto měly projekty většinou jasný fyzikální základ. A konec konců, v minulých ročnících se ukazovalo, že například o tom, jak zapojit tranzistor jako zesilovač, mají středoškoláci často jen matnou představu. Seznámení s elektronikou tedy také neškodí.
Některé z projektů představili na Veletrhu nápadů sami účastníci. (Příkladem je rádio – projekt, který získal v závěrečné anketě účastníků první místo. Za zmínku stojí, že jeho autoři nebyli žádní radioamatéři a do té doby nepostavili ani krystalku.) Několik dalších projektů je stručně popsáno dále.
Chaos (autor: Jan Kulveit)
Pojem deterministický chaos je už řadu let velice módní. Na počítačích umí chaotické děje modelovat kdekdo. Horší je to s experimenty. V chaotickém režimu může kmitat třeba dvojkyvadlo – jenže jak ho udělat bez tření?
I pohyb jednoduchého kyvadla může dávat chaotické výsledky, zařídíme-li jeho vhodné buzení. V realizovaném experimentu se lehounké kyvadlo (kousek plastikové trubky na špejli) odráželo poblíž dolní rovnovážné polohy od membrány reproduktoru buzeného střídavým napětím o frekvenci 50 Hz. Šlo o školní zdroj, napětí bylo zvoleno 1 V. Při impedanci reproduktoru 4 Ω jde o výkon 0,25 Ω, což na dané frekvenci sluch příliš neobtěžuje.
Periodu kyvadla je možno měnit změnou jeho délky. Bylo možno sledovat jak téměř periodický, tak výrazně chaotický pohyb. V chaotickém režimu se doba mezi po sobě následujícími nárazy na membránu reproduktoru výrazně a „nepředvídatelně“ měnila.
Autor realizoval ještě optický snímač, který propojil s portem počítače a dobu mezi průchody kyvadla snímačem měřil a vyhodnocoval počítačem. Podobně zaznamenával i další děj, který může být chaotický: intervaly mezi po sobě následujícími pády kapek vody z vhodně nastaveného vodovodního kohoutku.
Poučení z (téměř) Foucaultova kyvadla
Změřit rotaci Země je výzva, a tak u účastníků našel ohlas i ambiciózní projekt Foucaultova kyvadla. Předem konstatujme, že se nezdařil, jak bylo zamýšleno, ač mu realizátoři věnovali značné úsilí a velká láhev naplněná vodou nebo pískem visící na závěsu z druhého patra vzbuzovala i značné naděje. Útlum kmitů se však nakonec v reálných podmínkách ukázal příliš velký.
Navíc zde rušivě působil další efekt, který jsme předem neočekávali. Zřejmě si jej neuvědomuje ani řada dalších lidí, i když za sebou mají vysokoškolský kurs mechaniky.
Při teoretické analýze problému se předpokládá, že kyvadlo se kýve v jedné rovině. Reálně je ovšem značný problém vypustit na začátku kyvadlo tak, aby nemělo žádnou rychlost „do strany“. Při pohledu shora tedy většinou není trajektorií kyvadla úsečka, ale spíše elipsa.
První (a jak se ukázalo neadekvátní) reakcí na tento problém je říci: „To nevadí. Tak se místo roviny kyvu bude stáčet celá elipsa. Nebýt rotace Země, tak by se nestáčela. Je to přece stejné jako u skládání kolmých kmitů stejné frekvence…“
Kde je chyba v této úvaze? Při skládání kolmých kmitů se opravdu elipsa nestáčí. Kdyby kmity kyvadla šlo popsat jako harmonické kmity ve dvou kolmých směrech, bylo by tomu stejně. Jenže tak je tomu jen pro nekonečně malé výchylky! Ve skutečnosti je kyvadlo anharmonický oscilátor. Namodelujeme-li jeho pohyb na počítači, zjistíme, že nekýve-li kyvadlo přesně v jedné rovině, stáčí se. (Viz obrázek 1, který je výsledkem modelu zapsaného v systému Famulus. Model bude dostupný na webu na stránkách věnovaných příspěvkům Veletrhu nápadů 5.)
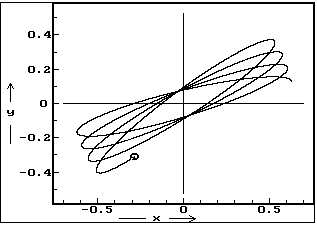
Obr. 1
Zdůrazněme, že jde o stáčení vůči inerciálnímu systému! Při pohledu shora není tedy trajektorií kyvadla elipsa, ale spíše růžice. Stáčení je větší pro větší odchylky od rovinného kývání (tedy pro „tlustší“ elipsy) a pro větší amplitudy rozkyvu.
U Foucaultova kyvadla musíme popsaný rušivý vliv co nejvíce eliminovat. To znamená vypouštět kyvadlo tak, aby kývalo co nejpřesněji v jedné rovině a mělo jen malou úhlovou amplitudu rozkyvu. Protože ale chceme spolehlivě naměřit stáčení roviny kyvu dané rotací Země, potřebujeme, aby kyvadlo vykývlo dostatečně daleko. Takže už je jasné, proč se závěs Foucaultova kyvadla dělá co nejdelší. Dalším důvodem bude zřejmě skutečnost, že delší závěs znamená delší periodu, a tedy při daném rozkyvu nižší rychlosti – a nižší rychlosti menší odpor prostředí…
Rotaci Země jsme sice nenaměřili, ale naučili jsme se toho dost.
Netlumené kmity kyvadla (autoři: E. Arazimová, J. Dvořák, V. Koudelková, vedl L. D.)
Kyvadlem byla velká matice zavěšená na dvou nitích délky asi 1 m. (Závěs ve tvaru písmene „V“ zajistí, že kyvadlo kýve v jedné rovině.) Pod kyvadlem byl umístěn elektromagnet tvořený třemi hřebíky omotanými několika desítkami závitů ze zvonkového drátu. Když se matice přibližuje k rovnovážné poloze, elektromagnet ji přitahuje a dodává tak energii ke krytí ztrát daných odporem vzduchu a dalšími vlivy. Jakmile kyvadlo projde rovnovážnou polohou, je ovšem třeba elektromagnet na chvíli vypnout, aby pohyb zase nebrzdil.
O vypnutí proudu do elektromagnetu se stará jednoduchá řídící elektronika. Průchod matice rovnovážnou polohou detekuje světelná závora tvořená infračervenou svítivou diodou a fototranzistorem. (Lze koupit v prodejnách s elektronickými součástkami už jako k sobě patřící dvojici. Výhodou je, že tato optická závora funguje na vzdálenost přes 10 cm bez jakékoli další optiky i na běžném denním světle.) Při zastínění fototranzistoru (tj. při průchodu kyvadla rovnovážnou polohou) se tranzistor T1 zavře (nevede). Do báze tranzistoru T2 pak teče dostatečně velký proud k tomu, aby se tranzistor T2 plně otevřel. Přes něj se prakticky na plné napětí baterie nabije kondenzátor C (viz další část schématu).
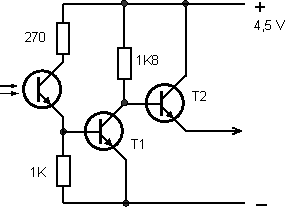
Obr. 2
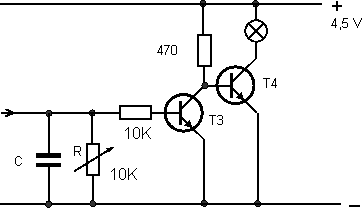
Obr. 3
Z nabitého kondenzátoru C teče proud do báze tranzistoru T3, který se proto otevře a fakticky zkratuje bázi tranzistoru T4 na zem (záporný pól baterie). Tranzistor T4 se tedy zavře a přestane jím procházet proud. Žárovka zhasne.
Kondenzátor se pomalu vybíjí jednak proudem do báze T3 a hlavně přes nastavitelný rezistor R (potenciometr 10 kΩ zapojený jako reostat). Až napětí klesne pod asi 0,7 V, T3 se zavře a T4 opět otevře a proud začne procházet. V zapojení byl použit elektrolytický kondenzátor o kapacitě 220 μF. S ním je pro dané odpory rezistorů doba vypnutí proudu maximálně něco přes 1 s. Rezistorem R ji lze nastavit dle potřeby kratší. (Pozn.: R se nesmí nastavit na nulový odpor, aby se velkým proudem nezničil tranzistor T2. Aby to nenastalo omylem, je vhodné do série k R připojit rezistor o hodnotě např. 100 Ω.)
Ve schématu není zakreslen elektromagnet. Ten se zapojí v kolektoru tranzistoru T4 do série s žárovkou, která omezí protékající proud. (Pozn.: Žárovka byla běžná 3,5 V/0,3 A. Paralelně k elektromagnetu je třeba zapojit diodu zapojenou v nepropustném směru. Dioda omezí špičku napětí indukovanou v cívce elektromagnetu při vypnutí proudu. Tato špička napětí by jinak hrozila zničit tranzistor T4.)
Použité součástky nejsou kritické; pouze tranzistory T2 a T4 musí vydržet kolektorový proud řádu stovek mA. (Byl použit typ KF507.) Je vhodné „oživovat“ každou část zapojení zvlášť. Obě části lze samozřejmě využít i nezávisle k samostatným experimentům.
Jak na tranzistory – aneb chvála prkének a mosazných hřebíčků
Při projektech se ukázalo, že řada účastníků začíná s elektronikou skutečně od začátku. Bylo třeba s nimi probrat, proč se ke svítivé diodě zapojuje do série rezistor (a jak velký), jak funguje tranzistor jako spínač, jak jako zesilovač v zapojení se společným emitorem atd.
Jednoduchá zapojení ilustrující dané funkce samozřejmě bylo třeba realizovat a vyzkoušet. Příkladem je zapojení na obrázku 4, na němž se demonstruje funkce tranzistoru jako spínače – po spojení svorek žárovka svítí. Připojíme-li mezi svorky proměnný odpor, např. ze starého potenciometru 10 kΩ, můžeme ukázat, jak se tranzistor postupně otvírá: při různě velkých proudech do báze svítí žárovička s různým jasem.
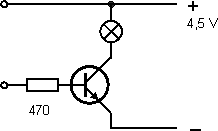
Obr. 4
Dalším příkladem, který zaujal, je zapojení podle obrázku 5. Díky vysokému proudovému zesilovacímu činiteli (jde o tzv. Darlingtonovo zapojení tranzistorů) umožňuje demonstrovat i průchod proudu lidským tělem. Aby se žárovka rozsvítila, stačí svorky spojit třeba nasliněnými prsty. (Ale nespojujte je drátem nebo rezistorem o malé hodnotě odporu; zničili byste tranzistory velkým proudem.)
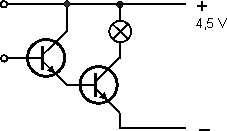
Obr. 5
Jak taková jednoduchá zapojení názorně realizovat? Velice užitečná se ukázala technologie, která je prý velice stará [2] a která objasňuje, proč se někdy mluví o zapojení „na prkénku“.
Základem jsou opravdu odřezky prkének z měkkého dřeva. Ideální jsou palubky, ty se dají dokonce spojovat vedle sebe. Dalším důležitým prvkem jsou malé mosazné hřebíčky. Mohly by být i měděné, podstatné je, aby na ně šlo dobře pájet pistolovou páječkou.
Hřebíčky, zatlučené ve vybraných místech do prkénka, tvoří pájecí body, k nimž se letují vývody součástek a spojovací dráty. Celé zapojení tak na prkénku vypadá přesně jako ve schématu, je velice názorné a lze je i jednoduše měnit. Na prkénko lze i psát a označovat tak například důležité body jako přívod napětí od zdroje, vstup, výstup atd.
Na prkénku lze vytvořit konstrukce triviální i složitější. Na táboře jsme tímto způsobem realizovali výše popsanou „řídící elektroniku k netlumenému kyvadlu“, zesilovač k reproduktoru (ten postupně košatěl od jednoduchého emitorového sledovače až po dvoustupňový zesilovač s dvojčinným koncovým stupněm), již zmíněné rádio a v neposlední řadě astabilní multivibrátor s časovačem typu 555.
Láce, přehlednost a flexibilita jsou důvody, pro něž lze tuto technologii vřele doporučit.
Literatura
[1] Dvořák L.: Pár věcí z tábora II – tentokrát o světle. In: Sborník z konference Veletrh nápadů učitelů fyziky 4, Příbram 1999. Ed. K. Rauner. ISBN 80-7082-576-6. ZČU Plzeň 1999. s. 35–38
[2] Žilavý P.: ústní sdělení
