Klasické a inovované měření rychlosti zvuku
Jiří Tesař
Anotace: Možnosti měření rychlosti zvuku ve fyzikálním praktiku – Kundtova trubice, Quinckeho trubice, srovnání fáze zvukového vlnění s referenčním zdrojem
Ve školní praxi se nejčastěji k měření rychlosti zvuku používají Kundtova a Quinckeho trubice. Další podobná metoda spočívá ve srovnání fáze zvukového vlnění s referenčním zdrojem. Základní myšlenkou všech těchto měření je určit vlnovou délku a frekvenci měřeného zvuku a pomocí vztahu v = λ . f lze potom určit rychlost šíření zvuku. Jejich princip je z fyzikálního hlediska odlišný, a tak je vhodné, např. ve fyzikálním praktiku, tyto metody použít jako navzájem se doplňující.
Ukažme si nejprve základní provedení, princip a některé modifikace Kundtovy trubice. Kundtova trubice je skleněná trubice, která má na jednom konci zdroj zvuku a druhý konec je uzavřen pomocí pohyblivého pístu. Zvuk se šíří trubicí od zdroje a na druhém konci se odráží s opačnou fází a při vhodné poloze pohyblivého pístu dochází ke vzniku stojatého vlnění.
Z teorie vyplývá, že vzdálenost mezi dvěma sousedními uzly nebo kmitnami je rovna polovině vlnové délky, musíme tedy nějakým způsobem „zviditelnit“ místa v trubici, kde jsou kmitny resp. uzly. K tomuto účelu se v klasickém měření (obr. 1) používá korková drť, která se v trubici rozkmitá - v místech kmiten rychlosti je korkový prášek rozmetán a v místech uzlů rychlosti zůstává v klidu*). Experimentátor tak může zřetelně určit uzle a kmitny rychlosti. Protože přesné určení kmity, resp. uzlu je velmi obtížné, je z hlediska přesnosti měření výhodné určit vzdálenost co nevětšího počtu např. uzlů a z tohoto údaje určit vlnovou délku měřeného zvuku.
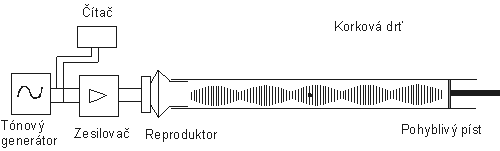
Obr. 1
Frekvenci měřeného zvuku určíme v případě, že jako zdroj zvuku používáme reproduktor připojený k tónovému generátoru, snadno pomocí čítače připojeného k tónovému generátoru. V případě, že jako zdroj zvuku používáme kovovou tyč (obr. 2), kterou podélně rozkmitáme, dostáváme zvuk o konstantní frekvenci (při daném upevnění tyče). Frekvenci tohoto zvuku určíme z rychlosti šíření zvuku v tyči**) a z její délky. Je-li tyč upevněna v jedné čtvrtině nebo ve třech čtvrtinách své délky je vlnová délka vydávaného zvuku rovna délce tyče, je-li tyč upevněna v polovině své délky je vlnová délka vydávaného zvuku rovna dvojnásobku délky tyče.
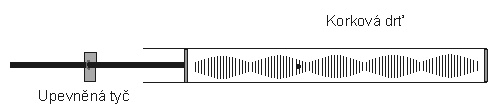
Obr. 2
Modifikace tohoto provedení spočívá v tom, že kmitny resp. uzly určujeme pomocí citlivého mikrofonu připojeného k osciloskopu. Stojaté vlnění vzniká v celém prostoru Kundtovy trubice - zvuk vychází z reproduktoru na jednom konci trubice a odráží se na uzavřeném konci na druhém konci trubice. Mikrofon připevníme do čela lehce pohyblivého segmentu připevněného k duté tyči, kterou procházejí vodiče od mikrofonu k osciloskopu (obr. 3). Protože segment neuzavírá celý průřez trubice, nedochází na něm k odrazu zvukové vlny a zvuk se odráží až na protější straně trubice. Pomalým posouváním mikrofonu v trubici můžeme pomocí výchylky na osciloskopu určit poměrně přesně místa, kde se nacházejí kmitny resp. uzly a z jejich vzdálenosti (případně ze vzdáleností dalších) vypočítat vlnovou délku zvuku.
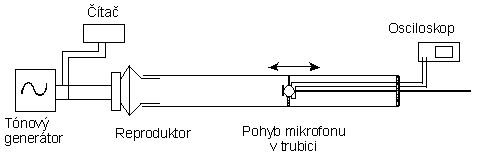
Obr. 3
K tomuto měření je možné využít Kundtovu trubici dodávanou v rámci ústředních dodávek Koménia na konci 80. let. Trubici opatříme výše uvedeným pohyblivým pístem s mikrofonem. Připojíme-li vestavěný zdroj zvuku (reproduktor) postupně k napětí 3, 5, 7 a 9 voltů, dostáváme zvuk o frekvenci 1440, 2877, 3983 a 4940 Hz.
Další způsob detekce kmiten, resp. uzlů je pomocí lékařského fonendoskopu bez kovové hlavičky. V uzlech je ticho, v kmitnách slyšíme pískot – viz [1].
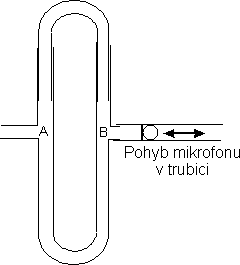
Quinceho trubice (obr. 4.) funguje na principu interferometru. Do místa A přivádíme zvuk o známé frekvenci od reproduktoru, který se rozděluje do dvou zvukovodů 1 a 2. Následně v místě B spolu obě zvuková vlnění interferují. V místě B umístíme citlivý mikrofon, který registruje výsledek interference.
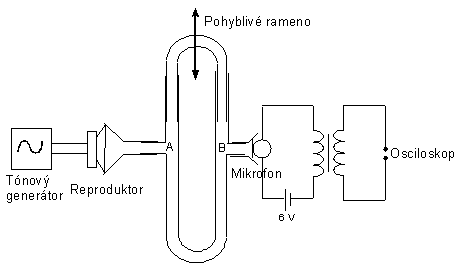
Obr. 4
Jsou-li délky zvukovodů stejné, nebo je-li rozdíl jejich délek Δl roven celistvému násobku vlnové délky zvuku, vzniká v místě B interferenční maximum intenzity zvuku, je-li rozdíl délek zvukovodů Δl roven lichému násobku poloviny vlnové délky zvuku vzniká v místě B interferenční minimum intenzity zvuku. Rozdíl délek zvukovodu dvou po sobě jdoucích minim nebo maxim je roven vlnové délce zvuku λ. Změnu délky zvukovodu provádíme jeho postupným vysouváním o vzdálenost d, protože zvukovod má dvě ramena, je dráhový rozdíl Δl = 2 . d.
Vzhledem k rozměrům školního provedení Quinckeho trubice, lze tuto metodu použít pro frekvence 2 kHz a vyšší, jejichž vlnová délka je přibližně rovna 17 cm. Při nižších frekvencích a při posuvu ramene Quinckeho trubice cca 15 cm se nepodaří zachytit dvě sousední interferenční minima nebo maxima.
Jestliže mikrofon připojíme k místu B přes gumovou nebo plastovou hadici, můžeme sledovat další zajímavý jev, který sice neovlivňuje výrazně výsledek měření, ale může přispět k upřesnění polohy interferenčního maxima resp. minima. Malý elektretový mikrofon, totiž uzavře výstup hadice, takže v ní dochází k o odrazu a následnému zesílení resp. zeslabení složeného zvuku. Než začneme měřit, musíme tedy pro danou vlnovou délku naleznout takovou polohu mikrofonu, kdy je amplituda vlnění na osciloskopu maximální (obr. 5).
Obr. 5
Poslední metodou, kterou se budu zabývat, je metoda spočívající ve srovnání fáze zvukového vlnění s referenčním zdrojem. Měření provádíme pomocí zařízení, které je znázorněno na obr. 6. Elektrický signál o frekvenci f z tónového generátoru je přiváděn na reproduktor a zároveň na x-výchylku osciloskopu. Z reproduktoru umístěného ve skleněné trubici se šíří zvuková vlna rovněž o frekvenci f k mikrofonu. Mikrofon tuto zvukovou vlnu převádí na napětí, které přivádíme na y-výchylku osciloskopu. Výsledkem složení těchto dvou signálů jsou Lissajouseovy obrazce, v našem případě se jedná o elipsy nebo úsečky, protože se jedná o signály se stejnou frekvencí.
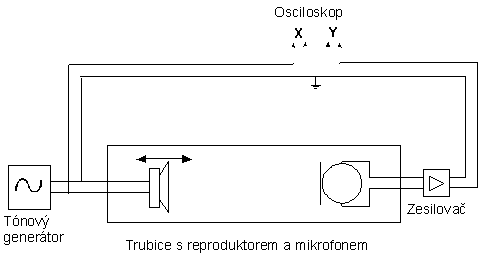
Obr. 6
Protože zvuk musí urazit vzdálenost d mezi reproduktorem a mikrofonem, je signál přicházející na y-výchylku osciloskopu fázově opožděn o φ za signálem přicházejícím na x-výchylku. Změnou vzdálenosti reproduktor – mikrofon (jejich vzájemným posuvem) dochází ke změně doby, za kterou překoná zvuk tuto vzdálenost, což se projeví změnou fázového posunu obou signálů φ a tedy i tvaru výsledného Lissajousova obrazce. Z teorie vyplývá, že v našem případě mohou mít Lissajousovy obrazce v závislosti na fázovém posunu tvary, které jsou na obr. 7.
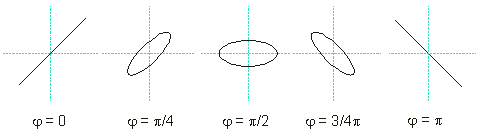
Obr. 7
Pro naše měření jsou důležité polohy reproduktoru a pístu, při nichž nastanou krajní případy Lissajousových obrazců, tj. kdy oba signály jsou ve stejné fázi (φ = 2kπ) nebo mají fázi opačnou (φ = (2k+1)π) - elipsa přechází v úsečku opačného sklonu. Vzdálenost mezi polohami reproduktoru pro oba krajní případy Lissajousových obrazců je tedy rovna polovině vlnové délky λ. Při měření posouváme reproduktor od výchozí polohy těsně u mikrofonu a zaznamenáváme jeho polohu v případě, že se na osciloskopu objeví úsečka, po dalším posunu se postupně objeví elipsy a následně úsečka, která však prochází jinými kvadranty. Posunutí mezi dvěma opačnými úsečkami je rovno polovině vlnové délky λ, posunutí mezi dvěma stejnými úsečkami je rovno vlnové délce λ.
Pro určení rychlosti zvuku můžeme použít i další metody – viz [2], pro běžnou praxi jsou však výše uvedené nejsnáze proveditelné a při stejném výchozím vztahu v = λ . f , se všechny opírají o odlišné fyzikální principy.
Použitá literatura:
[1] Baník, I., Baník, R.: Měření rychlosti zvuku netradičním způsobem, MFvŠ 10, č. 3, 1979
[2] Brož, J. a kol. Základy fyzikálních měření, SPN Praha 1983
[3] Lehotský, D. a kol.: Praktika z fyziky pre Pedagogické fakulty, SPN Bratislava 1967
[4] Stach, V., Tesař, J.: Fyzikální praktikum III., Pedagogická fakulta Č. Budějovice 1990
[5] Tögl, T. a kol.: Fyzikální praktikum, Západočeská univerzita v Plzni 2002
*) Kmitna akustického tlaku je oproti kmitně rychlosti posunuta o l/4, tj. v místech kmiten rychlosti jsou uzly tlaku a naopak.
**) Rychlost zvuku v materiálu, z něhož je tyč zhotovena nalezneme v tabulkách
