Fyzika jako zážitek
Miroslav Jílek
V příspěvku popisuji několik pokusů, které mohou sloužit k oživení hodin fyziky především na střední škole i k prohloubení pohledu na daný problém například v rámci různých fyzikálních seminářů, nebo kroužků. Pokusy jsem připravoval v rámci výuky fyziky na Gymnáziu Přípotoční v Praze a při vedení kroužků fyziky pro středoškolské studenty na MFF UK v Praze.
Odstředivá síla
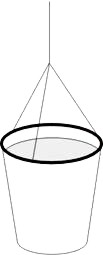
Obr. 1
Obdobu známého pokusu s kýblem a vodou, demonstrujícího účinky odstředivé síly, můžeme snadno provést s malým umělohmotným kelímkem a pevným provázkem.
Do horního okraje umělohmotného kelímku propíchneme symetricky tři otvory, pomocí kterých přivážeme kelímek k asi 0,5 m dlouhému provázku, viz obr. 1.
Kelímek naplníme téměř celý vodou, uchopíme konec provázku a roztočíme kelímek s vodou před sebou. Pokud si nacvičíme správné roztočení a zastavení kelímku, voda se po celou dobu nevylije. Pokus je samozřejmě zábavnější, pokud jej provádí někdo ze studentů.
Necháme studenty, aby se pokusily vysvětlit, proč voda z kelímku nevyteče ani v horní poloze, a můžeme hledat situace z běžného života, ve kterých se projevuje stejný jev – například pouťové atrakce, nejrůznější odstředivé stroje apod.
Pomocí pokusu můžeme také názorně vysvětlit rozdíl mezi inerciálními a neinerciálními systémy. V inerciálním systému třídy musíme působit na kelímek s vodou dostředivou silou, abychom ho přiměli pohybovat se po kruhové trajektorii, v opačném případě by se kelímek i voda pohybovaly přímočaře (neuvažujeme-li zakřivení vlivem gravitačního pole). Tuto sílu cítíme v ruce při točení kelímkem.
Z hlediska neinerciálního systému kelímku působí na vodu setrvačná odstředivá síla, která drží vodu v kelímku i v poloze dnem vzhůru (propíchneme-li do dna kelímku otvor, voda bude stříkat ven). Tato setrvačná síla působí pouze v rámci neinerciálního systému kelímku, v inerciálním systému ji nepozorujeme.
Na rozdíl od provádění tohoto pokusu s kýblem plným vody, nezpůsobí případné vylití vody z kelímku téměř žádné škody. Navíc se stává, že při provádění pokusu s kýblem se vlivem odstředivé síly utrhne ucho a odlétající kýbl může někoho zranit. Proto je lépe takovou variantu provádět někde venku, v dostatečné vzdálenosti od přihlížejících.
Střelba do špalíků
Klasickým příkladem na zákon zachování hybnosti a energie je určování rychlosti střely pomocí tzv. balistického kyvadla. Jinou možností, jak určit rychlost například diabolky, vystřelené ze vzduchovky, je změřit dráhu, kterou urazí po vodorovné podložce dřevěný špalík, do nějž jsme střelili.
Dřevěný špalík o hmotnosti M položíme na dřevěnou desku ležící na stole a zblízka do něj střelíme ze vzduchovky tak, aby se diabolka o hmotnosti m pohybovala pokud možno vodorovně. Dřevěný špalík se přitom posune o vzdálenost s.
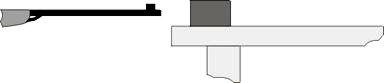
Obr. 2
Ze zákona zachování hybnosti vyplývá, že
![]() ,
,
kde v je hledaná rychlost diabolky, w je počáteční rychlost špalíku po zásahu. Tuto rychlost špalíku pak spočítáme ze zákona zachování energie – kinetická energie špalíku se „zavrtanou“ diabolkou po zásahu bude rovna práci třecích sil potřebných k zastavení špalíku.
![]()
g je tíhové zrychlení, f je součinitel smykového tření mezi špalíkem a podložkou.
Pro hledanou rychlost diabolky pak dostáváme z předchozích výrazů vztah:
![]()
Součinitel smykového tření f můžeme změřit některou z obvyklých metod, například měřením úhlu sklonu podložky, při kterém špalík sjíždí rovnoměrně po podložce dolů, viz [1]. Ostatní veličiny jednoduše zvážíme a změříme.
Pokus lze provádět demonstračně, i jako laboratorní cvičení pro jednotlivé skupiny studentů. Samozřejmě je potřeba dbát maximální bezpečnosti při manipulaci se vzduchovkou, a studenty s ní nechat manipulovat pouze pod dohledem vyučujícího. Teoretický vztah pro rychlost střely se mohou studenti pokusit odvodit sami. Při odvozování je podobně jako v případě balistického kyvadla vhodné zdůraznit potřebu použití zákona zachování hybnosti, nemůžeme použít pouze zachování energie, protože nedokážeme určit množství energie spotřebované na „zavrtání“ diabolky do špalíku.
Hmotnost dřevěného špalíku by měla činit asi 100 – 250 g. Lehčí špalíky se pohybují příliš rychle – „poskakují po podložce“, takže práce třecích sil se neprojevuje na celé dráze pohybu špalíku a výsledek je zkreslený. Při hmotnosti špalíku 200 g a hmotnosti diabolky 0,47 g se špalík posune po dřevěné podložce zhruba o 5 cm.
Pozn. Pokus jsem podrobněji zkoušel na semináři pro budoucí učitele fyziky na Malé Hraštici, viz [2].
Brownův pohyb
Jednoduchý pokus na kvalitativní pozorování Brownova pohybu lze provést s laserovým ukazovátkem a zkumavkou.
Do zkumavky nalijeme trochu vody s několika kapkami smetany do kávy, případně s trochou latexu pro vytvoření roztoku s Brownovými částicemi. Zkumavku upneme do jednoho chemického stojanu, laserové ukazovátko do druhého stojanu tak, aby laserový paprsek procházel skrz zakulacené dno zkumavky a dopadal na asi 2 – 3 m vzdálené bílé stínítko, viz obr. 3.
Laserový paprsek je rozšířen zkumavkou s roztokem jako spojnou čočkou, takže na stínítku vytvoří zvětšený obraz světelné stopy o průměru kolem 30 cm. Světlo laseru se přitom ohýbá na chaoticky se pohybujících částicích roztoku a na stínítku tak můžeme pozorovat zvětšený proměnný ohybový obrazec dokazující pohyb částic.
Vzhledem k nízké intenzitě laserového paprsku je vhodné pokus provádět při zatemnění. Zpočátku pokusu můžeme na stínítku pozorovat převládající jednosměrný pohyb, jak se smetana promíchává s vodou. Po uklidnění těchto proudů je vidět chaotický pohyb bez převládajícího směru.
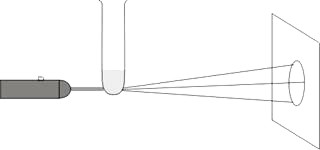
Obr. 3
Výhoda pokusu oproti sledování mikroskopem je možnost společného sledování jevu bez nákladných technických pomůcek.
Pozn. Námět na pokus jsem převzal z časopisu Physics Education, viz [3].
Rovnovážný stav
Další pokus je spíše zábavným přiblížením chování plynu z molekulárního hlediska.
K jeho přípravě potřebujeme dostatečné množství novinového papíru, ze kterého spolu se studenty „zmuchláme“ přibližně 50 – 100 papírových koulí. Třídu, její část, nebo například menší chodbu rozdělíme stolky, nebo židlemi na dvě stejné poloviny. Do obou polovin se postaví stejný počet studentů (počet volíme podle velikosti místnosti), alespoň jeden člověk musí zůstat mimo.
Všechny papírové koule na začátku umístíme do jedné poloviny. Jeden student, nebo učitel, stojící mimo obě poloviny, má stopky a odměřuje stejné časové intervaly například 5 s dlouhé. Jakmile výkřikem ohlásí začátek intervalu, studenti začnou vzájemně přehazovat papírové koule z jedné poloviny do druhé a naopak.
V okamžiku, kdy člověk se stopkami ohlásí například výkřikem „stop“ konec intervalu, musí všichni přestat házet. Potom studenti spočítají koule v každé polovině a výsledek někdo zapíše pro obě poloviny na tabuli.
Následuje další interval, ve kterém se studenti opět snaží přeházet co nejvíce koulí ze své poloviny do druhé. Je vhodné se například domluvit, že jeden člověk může najednou přehazovat vždy jen jednu kouli, a že se koule nesmějí srážet do druhé poloviny ze vzduchu. Výsledný počet koulí v obou polovinách po druhém intervalu se opět zapíše a „hra“ se opakuje, dokud není počet koulí v obou polovinách přibližně vyrovnaný v několika, po sobě jdoucích, intervalech.
Nakonec uklidíme všechny koule a pokusíme se vysvětlit analogii mezi tímto pokusem a chováním plynu. Papírové koule představují molekuly plynu, které jsou na začátku shromážděny v jedné polovině nádoby, oddělené přepážkou od druhé. Uvolníme li přepážku, molekuly se začnou vlivem svého chaotického pohybu a vzájemných srážek dostávat i do druhé poloviny (přehazování) a my můžeme v pravidelných intervalech sledovat jejich počet v obou částech systému. Pokud jsou podmínky v obou částech stejné (stejně zdatné skupiny „přehazovačů“, kteří nepodvádí a symetrické poloviny místnosti včetně možných překážek), počet molekul (koulí) se po nějaké době v obou částech zhruba vyrovná – dojde k termodynamické rovnováze systému.
Je zajímavé sledovat také průběh počtu koulí v jednotlivých částech v závislosti na čase a nakreslit graf této závislosti. Graf by měl mít zhruba exponenciální charakter, vzhledem k malému počtu koulí, velkému časovému intervalu a ne zcela symetrickým podmínkám může tato závislost vykazovat větší odchylky.
Pozn. Analogii pokusu s chováním plynu lze studentům samozřejmě vyložit před začátkem „hry“ při vysvětlování pravidel.
Pokud je jedna skupina v přehazování výrazně výkonnější než druhá, můžeme nechat studenty hledat analogickou situaci v reálném systému (například vyšší teplota plynu v jedné části bude znamenat jeho menší hustotu).
Diskusi odchylek naměřených hodnot od teorie v závislosti na celkovém počtu koulí (molekul) a další rozbory tohoto pokusu lze najít v [4].
Energie pružiny
Pokus je vhodný pro jednoduché přiblížení kvadratické závislosti energie pružiny na jejím prodloužení.
K provedení pokusu potřebujeme dvě stejné pružiny (například ze školních souprav pro studium kmitů), dva chemické stojany, asi 50 – 100 g těžkou kovovou kuličku, nebo podobný předmět, délkové měřítko (metr, dvoumetr…) a kousek tvrdého papíru, eventuelně kůže.
Jedny konce pružin spojíme páskem tvrdého papíru, nebo kůže a druhé konce připevníme k vedle sebe stojícím chemickým stojanům tak, že vytvoříme jednoduchý prak, kterým je možno vystřelovat kuličku kolmo vzhůru, viz obr. 4. Pružiny by měly být pokud možno rovnoběžné.
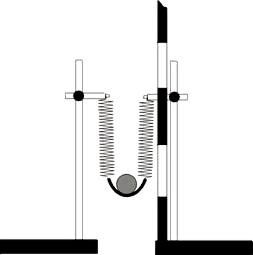
Obr. 4
Vedle pružin připevníme, nebo přidržíme délkové měřítko a poznamenáme si výšku dolního okraje pružin. Potom vložíme kuličku do praku, natáhneme pružiny o několik centimetrů a necháme kuličku vystřelit vzhůru. Sledujeme přitom do jaké výšky od své spodní polohy vyletěla a zaznamenáme si tuto hodnotu. Výšku můžeme sledovat na přistaveném měřítku, nebo si například zaznamenat výšku výstupu na blízké zdi a poté ji odměřit od spodní polohy kuličky při výstřelu.
Energie pružin, závisející kvadraticky na jejich prodloužení, se spotřebuje na změnu potenciální energie kuličky, závisející lineárně na výšce výstupu. Vzhledem k tomu by měla kulička při dvojnásobném prodloužení pružin vylétnout do čtyřnásobné výšky.
Pokus lze také provádět jako laboratorní cvičení na ověření vztahu pro energii pružiny, eventuelně jako doplňkový úkol při měření tuhosti pružin některou z obvyklých metod. Uvažujeme přitom samozřejmě, že tuhosti dvou pružin, tvořících prak, a tedy i jejich energie se při výstřelu sčítají.
Pozn. Je potřeba, aby hmotnost vystřelované kuličky byla dostatečně velká vzhledem k tuhosti použitých pružin. Při malé hmotnosti kuličky a velké tuhosti pružin se všechna energie pružin nepředá kuličce (pružiny po výstřelu příliš kmitají) a výsledek je zkreslen.
Pokus je možné provádět také s gumičkami (klasický prak), které však nemají ve větším rozsahu tak lineární elastickou charakteristiku jako pružiny.
Mírou předávání energie praku projektilu se zabýval J. Kekule v zajímavém příspěvku na Veletrhu nápadů učitelů fyziky v minulém roce, viz [5].
Faradayova klec
Jednoduchou variantu efektního pokusu dokazujícího účinky Faradayovy klece lze provést s Ruhmkorffovým transformátorem.
K pokusu potřebujeme kromě transformátoru kousek hadříku, líh, kleště s izolovanými rukojetěmi, nádobu s vodou a kousek hustého drátěného pletiva, nebo například drátěnou podložku pod varné chemické sklo.
Obdélníkový kousek drátěného pletiva ohneme do tvaru písmene „U“, případně vytvoříme z pletiva malou na jedné straně otevřenou klec. Kousek hadříku namočíme v lihu, vložíme ho do vytvořené klece a tu podržíme v kleštích mezi elektrodami jiskřiště transformátoru.
Po zapnutí transformátoru pozorujeme výboj mezi elektrodami, který směřuje skrz klec s hadříkem. Hadřík uvnitř přitom zůstane nezapálen, protože výboj probíhá po vnější stěně vodivé klece.
V druhé fázi pokusu uchopíme hadřík namočený v lihu do kleští a podržíme ho mezi elektrodami transformátoru bez klece. Po zapnutí transformátoru hadřík okamžitě vzplane – uhasíme ho v připravené nádobě s vodou.
Po pokusu můžeme se studenty diskutovat ochranu před bouřkou uvnitř automobilu, či jiných kovových konstrukcí i ochranu různých elektronických zařízení před silným elektrickým polem uvnitř kovové schránky.
Elektromagnetická indukce
Pomocí posledního pokusu lze snadno demonstrovat účinky elektromagnetické indukce, které můžeme cítit na vlastní kůži.
K pokusu potřebujeme cívku o 12 000 závitech s „U“ jádrem a velký podkovovitý magnet, dosedající na jádro – vše ze školní soupravy rozkladného transformátoru a dále dva vodiče.
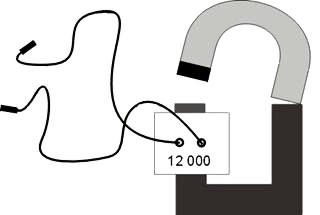
Obr. 5
Cívku navlékneme na jádro a připojíme k jejím vývodům dva vodiče. Druhé dva konce vodičů necháme někoho podržet v rukou a magnet přiklapneme k jádru tak, abychom vytvořili uzavřený magnetický obvod. Rychlé vytvoření magnetického pole v jádře při přiklapnutí magnetu indukuje v cívce s mnoha závity vysoké napětí, které pocítí osoba držící konce vodičů jako brnění.
Intenzita vjemu napětí závisí do značné míry na vlhkosti pokožky osoby, která drží vodiče, proto magnet přiklapujeme napoprvé pomalu, když je brnění příliš slabé, můžeme magnet přiklapnout silněji. Pokus si je vhodné dopředu vyzkoušet na sobě.
Studentům je také možné zadat problémovou úlohu, zda je při pokusu výhodnější mít suché ruce, nebo si je namočit do vody a jak tomu bude v případě, kdy se budou dva lidé držet za ruku a druhou volnou rukou budou držet konce vodičů.
V prvním případě, kdy drží vodiče jeden člověk je zřejmě výhodnější mít suché ruce, které znamenají velký přechodový odpor mezi vodičem a lidskou tkání a tedy i nižší proud tekoucí při daném indukovaném napětí obvodem s cívkou a „zapojeným člověkem“.
V druhém případě „sériového spojení dvou lidí“ proteče oběma účastníky pokusu stejný proud, úbytek napětí bude přitom větší na osobě s větším elektrickým odporem, tedy na osobě se suchýma rukama. Protože elektrická energie, způsobující podráždění nervů, uvolněná za konstantní čas je dána součinem napětí a proudu, ucítí v tomto případě silnější brnění osoba se suchýma rukama.
Podobně můžeme zkoumat také „paralelní zapojení dvou lidí“.
Literatura
[1] Bednařík, M., Široká, M.: Fyzika pro gymnázia – Mechanika. Prometheus, Praha 2000, Laboratorní cvičení 5.
[2] Jarní soustředění pro posluchače učitelství fyziky MFF UK a „spřízněné duše“ http://kdf.mff.cuni.cz/Hrastice/Hr2003/Hr03.htm
[3] Krulak, H.: Brownian motion with a laser. In: Physics Education, Volume 30, March 1999.
[4] Carson, S., R.: An interactive pupil demonstration of the approach to dynamic equilibrium. In: Physics Education, Volume 34, January 1999.
[5] Kekule, J.: Měření kinetické energie střely z praku. In: Sborník z konference Veletrh nápadů učitelů fyziky 7, Praha 2002. Ed. Svoboda, E., Dvořák, L., str. 168 – 171.
[6] Svoboda, E.: Pokusy z fyziky s jednoduchými pomůckami, Prometheus, Praha 1995.
