„Gravitační“ katapult
Jiří Bartoš, Pavel Konečný
Katapulty různé konstrukce jsou známy již od starověku. Doba jejich největší slávy byla zdánlivě v době existence Římské říše, a to hlavně díky historickému filmu. Zdá se, že Římané nepoužívali nejefektivnější druhy katapultů, jejich stroje byly obvykle založeny na principu přeměny potenciální energie pružnosti na energii kinetickou katapultovaného tělesa. Je ovšem pravda, že tyto katapulty byly jak z hlediska konstrukce, tak z hlediska odladění na optimální výkon podstatně jednodušší.
V tomto příspěvku budeme hovořit o konstrukci mírně složitější, ale o to efektivnější. Zvláštností tohoto katapultu je, že byl užíván k dobývání opevněných měst zdánlivě méně vyspělým národem, a to Mongolskými kmeny při obsazování středního východu v 12-13.století. Přibližně v téže době se objevil jako bojový prostředek i v Evropě, zvláště ve Francii. Ovšem ani jednomu ze jmenovaných národů nepatří prvenství v užití tohoto stroje. TREBUCHET, jak se tomuto katapultu ve světě říká, je vynálezem čínským z doby přibližně 300 let př.n.l.
Náš katapult je principiálně založen na přeměně potenciální tíhové energie „těžkého“ tělesa na kinetickou energii tělesa lehčího, velmi přesvědčivě tak dokumentuje zákon zachování mechanické energie. Poměr hmotností těles ![]() se pohybuje v rozmezí 20 až 100.
se pohybuje v rozmezí 20 až 100.
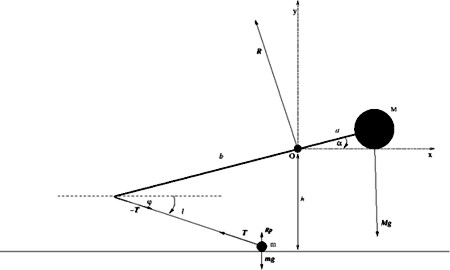
Pro náš experiment jsme sestavili katapult laboratorních rozměrů, který je možné použít i v místnosti, z materiálu, který je přístupný v každém fyzikálním a chemickém kabinetě (viz. obr.1 a rozměry katapultu), kde M=1 kg a m=0,01 kg.

Obr. 1
Pro zjednodušení výpočtů přijmeme tyto předpoklady:
O … pevná osa
M … těžké závaží (olověné broky) spolu s nehmotnou tuhou tyčí
m … katapultované těleso (pytlíček s pískem) na vlákně (nepružném, nehmotném, ohebném)
g … tíhové zrychlení
α, φ … zobecněné souřadnice
T … tahová síla ve vlákně
mg .. tíhová síla působící na katapultované těleso
Mg … tíhová síla působící na těžké těleso
R … reakční síla působící na osu
RP…reakční síla působící na katapultované těleso od podložky
Rozměry katapultu:
a = 0,093 m
b = 0,407 m
l = 0,301 m
h = 0,350 m
Souřadnice těžkého tělesa budeme označovat X, Y ; katapultovaného tělesa x, y.
Ještě než začneme s matematickým popisem pohybu katapultu, popíšeme kvalitativně pohyb obou těles.
Těžiště „těžkého“ tělesa opisuje část kružnice se středem v bodě O. Pohyb katapultovaného tělesa rozdělíme do tří fází. V první se pohybuje po podložce směrem vzad vzhledem ke směru „výstřelu“, tj. pouze ve směru osy x. V druhé fázi se oddělí od podložky a pevně spojené pomocí vlákna s koncem ramene vykonává pohyb po trajektorii, jejímž numerickým popisem se budeme později zabývat, a v jistém okamžiku se odpojí i s vláknem od ramene katapultu. Třetí fáze je pouze otázkou vnější balistiky, v našem případě šikmého vrhu.
Fáze první:
Obr. 2
![]()
![]()
Zároveň platí podmínka pro pohyb katapultovaného tělesa pouze v ose x, tj. ![]() a úhel a nabývá v situaci, kdy je „těžké“ těleso nad osou x, záporných hodnot.
a úhel a nabývá v situaci, kdy je „těžké“ těleso nad osou x, záporných hodnot.
Pohybové rovnice:
Pro katapultované těleso m:
![]()
Pro „těžké“ těleso M (II.impulzová věta vzhledem k bodu O):
![]()
Numerické řešení rovnic (3) a (4) využijeme pro získání počátečních podmínek
![]() pro druhou fázi pohybu katapultovaného tělesa, tj. pro okamžik oddělení katapultovaného tělesa od podložky, který je dán podmínkou
pro druhou fázi pohybu katapultovaného tělesa, tj. pro okamžik oddělení katapultovaného tělesa od podložky, který je dán podmínkou ![]() (
(![]() ), vyplývající z pohybových rovnic (3).
), vyplývající z pohybových rovnic (3).
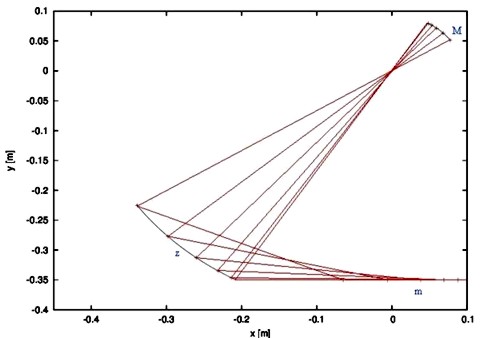
Obr. 3
Na obr.3 vidíme tři křivky, představující trajektorie „těžkého“ tělesa (M), konce ramene (z), na němž je uchyceno vlákno spojující rameno s katapultovaným tělesem, a katapultovaného tělesa (m). Spojnice mezi křivkami představující polohy ramena a vlákna rozdělují pohyb katapultu na pět stejných časových intervalů.
Fáze druhá:
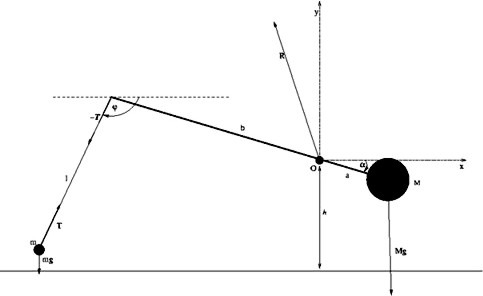
Obr. 4
Ve druhé fázi pohybu zůstávají v platnosti vztahy (1) a (2). V této fázi se již katapultované těleso pohybuje po trajektorii získané řešením rovnic (5) až (7).
Pohybové rovnice:
Pro katapultované těleso m:
![]()
Pro „těžké“ těleso M:
I.impulzová věta:
![]()
II.impulzová věta (vzhledem k bodu O):
![]() (7)
(7)
Numerickým řešením rovnic (5) až (7) získáme veškeré informace o systému, tedy tvar trajektorie, rychlosti jednotlivých součástí katapultu, atd.
Modelovaný katapult je svými rozměry optimalizován tak, aby katapultované těleso vstupovalo do třetí fáze pohybu (šikmého vrhu) s ideálním elevačním úhlem, tj. π/2. Je však nutné vhodně nastavit sklon háčku na němž je zavěšeno vlákno s katapultovaným tělesem.
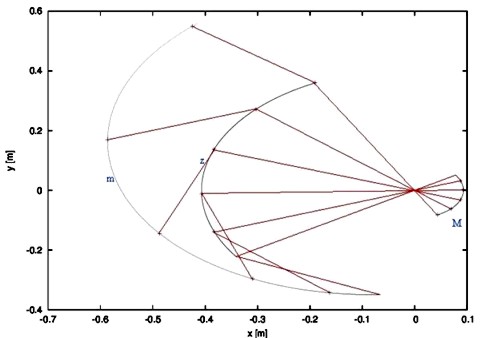
Obr. 5
Na obr.5 vidíme opět trajektorie „těžkého“ tělesa (M), konce ramene (z) a katapultovaného tělesa (m). Spojnice mezi křivkami znovu reprezentují polohy katapultu a rozdělují jeho pohyb na pět stejných časových intervalů.
Třetí fáze:
Zde snad již nemá význam psát známé pohybové rovnice a je možné zmínit se o vztahu pro dolet katapultovaného tělesa, tj. ![]() , kde θ je elevační úhel a v0 je počáteční rychlost.
, kde θ je elevační úhel a v0 je počáteční rychlost.
V našem případě činí v0 = 14 ms-1 a dolet d = 20 m. Tyto hodnoty jsou vypočtené za všech výše uvedených předpokladů. Důležitým parametrem je ještě výškový dostup, který činí θ = 5,5 m. Vypočtená účinnost katapultu je η = 71%. Reálné hodnoty se ovšem od vypočtených výrazně liší, to je způsobeno ztrátami v mechanizmu (v0 = 10 ms-1 ; d = 10 m ; q = 4 m ; h = 35%) , tj. s katapultem těchto rozměrů je skutečně možné střílet v běžné přednáškové místnosti.
Literatura:
[1] http://home.att.net/~wjahsman-mta/RetroMechanics.pdf
