Netradiční měřicí přístroje 3
Leoš Dvořák
I letos jsou tématem „Netradičních měřicích přístrojů“ spíše indikátory: ● indikátor malých napětí, který umožní demonstrovat například elektromagnetickou indukci při pohybu vodiče v zemském magnetickém poli, ● jednoduchá konstrukce pro demonstraci ohybu kolejí za horka a ● jednoduchý dilatometr pro ukázku tepelné roztažnosti materiálů.
Předností všech uvedených „přístrojů“ jsou malé výrobní náklady: U prvního indikátoru pár desítek korun, u dalších dvou opravdu jen pár korun. Druhé dva indikátory si mohou lehce zhotovit i sami žáci.
Indikátor malých napětí
Dále popsaný přístroj indikuje malá napětí změnou jasu žárovičky: jedné polaritě odpovídá zvýšení jasu, opačné polaritě snížení jasu.
K čemu může být takový indikátor dobrý?
Například k demonstraci elektromagnetické indukce při pohybu magnetu v blízkosti vodiče. Obvykle se to demonstruje pomocí cívky o mnoha závitech. Nešlo by to však s jedním závitem?
Jednoduchý odhad ukáže potřebnou citlivost. Magnetická indukce v blízkosti běžných malých feritových magnetů dosahuje hodnot setin tesla. Je-li plocha magnetu 1 cm2, je velikost magnetického indukčního toku (který odhadneme jako Φ = B·S) řádu jednotek 10-6 Wb. Indukované napětí je dáno časovou změnou indukčního toku. Posuneme-li magnet nad závit a zpět několikrát za sekundu (tedy doba časové změny Δt bude řádu desetin s), bude přibližně ![]() . Potřebná citlivost našeho indikátoru by tedy měla dosahovat 10 mikrovoltů. Samozřejmě můžeme užít silnější magnet či magnet s větší plochou, rozhodně však jsme pod mezí citlivosti běžných multimetrů.
. Potřebná citlivost našeho indikátoru by tedy měla dosahovat 10 mikrovoltů. Samozřejmě můžeme užít silnější magnet či magnet s větší plochou, rozhodně však jsme pod mezí citlivosti běžných multimetrů.
S moderními elektronickými součástkami však dokáže dostatečně citlivý indikátor postavit snad každý, kdo se trochu věnoval „kutění“ v oblasti elektroniky či radiotechniky. Principiální schéma indikátoru je na obr. 1.
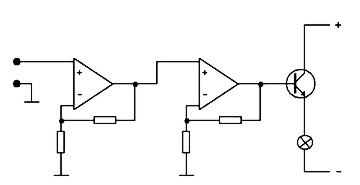
Obr. 1: Principiální schéma indikátoru.
Je použit dvojitý operační zesilovač typu TLC272 (který lze v obchodech se součástkami koupit za cenu něco přes dvacet korun), jeho výstupní proud zesiluje tranzistor zapojený jako emitorový sledovač. Protože celkové stejnosměrné zesílení je značné (náš indikátor bude zesilovat více než 40 tisíc-krát), způsobila by i malá vstupní napěťová nesymetrie (kterou nutně integrovaný obvod vykazuje), že žárovka by buď svítila naplno, nebo byla zcela zhaslá. Proto je indikátor doplněn ještě potenciometrem, jímž lze nesymetrii korigovat a jas žárovky nastavit na mírný svit. Celkové zapojení indikátoru je na obrázku 2.
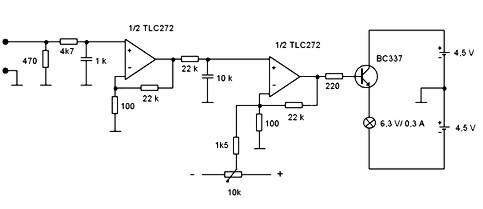
Obr. 2: Celkové zapojení indikátoru malých napětí
V zapojení jsou navíc i RC členy omezující střídavé signály, zejména vysokofrekvenční. (Při vysokém zesílení by jinak mohly např. signály středovlnných vysílačů, indukované do závitu na vstupu, působit potíže.) Celé zapojení stačí napájet ze dvou plochých baterií; napájení samotného integrovaného obvodu není zakresleno. Vývody potenciometru označené + a – se připojí k napětí +4,5 V a -4,5 V z plochých baterií. Na vstupní svorky (ve schématu zcela vlevo) se připojí závit z drátu, cívka nebo přívody spojené se nějakým experimentem, v němž chceme indikovat malé napětí.
Náměty na experimenty s indikátorem malých napětí
Demonstrace elektromagnetické indukce – pohyb magnetu v blízkosti vodiče
Stačí vstupní svorky spojit kusem drátu nebo kablíku. Při pohybu magnetem kolmo k drátu (tak, že siločáry „při svém pohybu protínají drát“) žárovička jasněji zazáří, při pohybu opačným směrem její jas pohasne. S tím, co žákům ilustrovat a zdůraznit, si už každý správný učitel fyziky jistě „pohraje“ sám. Může třeba ukázat, že: – při rychlejším pohybu je změna jasu výraznější, při pomalém sotva znatelná, – pohyb magnetu ve větší vzdálenosti působí menší změnu, – indikátor reaguje výrazněji, smotáme-li drát do dvou, třech a více závitů („ejhle, vzniká cívka!“), – připojíme-li ke vstupním svorkám indikátoru cívku o větším počtu závitů, reaguje přístroj i na velmi malé změny magnetického pole, – jádro v cívce ještě zvětší citlivost (s cívkou 1200 závitů z rozkladného transformátoru reaguje indikátor na otáčení silnějším magnetem ve vzdálenosti přes dva metry), atd.
Se středoškoláky (alespoň s těmi, které zajímá fyzika) lze diskutovat o tom, že se zde vskutku uplatňuje změna magnetického toku závitem (působivé je třeba užít závit o průměru přes jeden metr a uprostřed otáčet silnějším magetem). Spíše do úvodního VŠ kurzu už patří diskuse o tom, že indukce pole magnetického dipólu klesá s třetí mocninou vzdálenosti a že tedy dvakrát vyšší počet závitů cívky neznamená, že můžeme detekovat pohyby magnetu do dvakrát vyšší vzdálenosti. Naopak i na nižší než středoškolské úrovni lze předvést princip záznamu na magnetický pásek: „potíráním“ magnetem různě zmagnetujeme různé kusy kovového svinovacího dvoumetru a pak jej protahujeme nad cívkou připojenou k indikátoru. Jde o známý pokus, ale náš indikátor ho umožní demonstrovat velmi výrazně. Určitě se objeví i další nápady…
Demonstrace elektromagnetické indukce – pohyb vodiče v magnetickém poli
Analogicky k předchozím pokusům můžeme samozřejmě nechat magnet v klidu a pohybovat vodičem. I zde lze demonstrovat, že indukované napětí je největší, když je vodič kolmo na siločáry a také se kolmo na siločáry pohybuje.
Citlivost indikátoru umožní demonstrovat indukované napětí i při pohybu vodiče v zemském magnetickém poli. Stačí ke vstupním svorkám připojit delší ohebný kablík a točit jím podobně, jako švihadlem. Dokonce tak lze (velmi přibližně) hledat severojižní směr a sklon magnetických siločar vůči vodorovné rovině: je-li vodič rovnoběžný se směrem siločar, neindukuje se v něm při jeho pohybu napětí. (V praxi ovšem díky nehomogenitám magnetického pole způsobeném třeba blízkými železnými předměty bude indikátor na pohyb vodiče vždy trochu reagovat, ale výrazně méně, než když je vodič kolmo k siločarám.)
S pokročilejšími studenty lze počítat, jaké napětí se na pohybujícím se vodiči indukuje. Hodnota magnetické indukce zemského magnetického pole (její horizontální složka je přibližně B=2·10-5 T) pak dostane mnohem konkrétnější smysl – na metr vodiče kolmého k siločarám, pohybujícího se (rovněž kolmo k siločarám) rychlostí 1 m/s, se indukuje napětí zhruba 20 mikrovoltů. A to náš indikátor pohodlně ukáže.
Demonstrace termoelektrického napětí
Citlivost indikátoru umožní snadno ukázat termoelektrické napětí dané rozdílem teplot na konci vodiče (připojeného k vodičům z jiného materiálu). Ze údajů ve středoškolských tabulkách například lehce odvodíme, že termočlánek vzniklý spojením cínu a mědi dává napětí 0,3 mV při rozdílu teplot jeho spojů 100 K. To znamená napětí 3 mikrovolty na stupeň. Zahřátí jednoho spoje v prstech tedy stačí k vytvoření napětí výrazně přes deset mikrovoltů, které náš indikátor spolehlivě ukáže. Pro rychlou demonstraci stačí připojit ke kablíkům od vstupních svorek kus drátu z jiného materiálu (třeba železa, hliníku, cínu apod.) a jeden konec zahřát v prstech. Pak ho necháme vychladnout a zahřejeme zase druhý konec… Pokud použijeme konstantanový drát, bude reakce indikátoru velmi výrazná a rychlá – na spoj stačí doslova jen dýchnout.
Kdybychom chtěli termoelektrické napětí alespoň zhruba kvantitativně měřit, museli bychom náš indikátor okalibrovat. Není to tak těžké, jak by se na první pohled mohlo zdát. Stačí k ploché baterii připojit resistor o odporu necelých 5 megaohmů (běžně se prodávají resistory s odporem 4,7 MΩ) a do série s ním resistory 10 Ω, 20 Ω, atd. Poteče jimi proud asi 1 μA, takže na nich bude právě napětí 10 μV, 20 μV, … Tato napětí můžete přivést na indikátor, změnu jasu žárovky si zhruba zapamatovat a podle ní pak při experimentech odhadovat „měřené“ napětí.
Pro ještě přesnější (už „skoro opravdové“) měření malých napětí bychom mohli na výstup našeho indikátoru připojit malý multimetr (mezi „zemnicí bod“ spojující ploché baterie ve zdroji a emitor tranzistoru připojený k žárovce). Uděláte-li to, nebuďte překvapeni, že napětí kolísá a pomalu se mění („ujíždí“). To se projevuje šum a nedokonalá tepelná stabilita našeho přístroje. Řádově citlivější už náš jednoduchý indikátor asi neuděláme…
Demonstrace spádu napětí na vodiči
Všichni víme, že pro vodiče platí Ohmův zákon. Na vodiči, jímž protéká proud I je tedy nutně úbytek napětí U=I·R. Úbytky napětí na dostatečně tlustých vodičích při dostatečně malých proudech ovšem běžně zanedbáváme. Přece – jaký by mohl být úbytek napětí na kousku měděného drátu o průměru třeba 2 mm, jímž teče například do žárovičky proud nějakých 200 mA? Náš indikátor nám to umožní změřit.
Schéma zapojení, zahrnující v sérii plochou baterii, žárovičku a tlustý drát, ani není třeba kreslit. K drátu připojíme krokosvorkami přívody od vstupních svorek indikátoru. Po zapnutí proudu indikátor ukáže, že spád napětí na drátu je opravdu řádu desítek mikrovoltů. (Lze ukázat spád napětí už na jednom centimetru drátu.)
Chceme-li, můžeme samozřejmě se žáky ověřit výpočtem, že odpor 1 cm daného drátu je asi 50 milióntin Ohmu. Při proudu 0,2 A je tedy úbytek napětí asi 10 mikrovoltů – a to už indikátor ukáže. Diskuse o tom, kolik činí úbytek na několika metrech takového drátu při proudu 10 A (který teče třeba ze sítě do varné konvice) už může následovat. A to nemluvíme o proudech při zkratu nebo o proudu tekoucím do do automobilového startéru při startování auta.
Výhody a nevýhody indikátoru se žárovkou
Zkusme zhodnotit náš indikátor trochu obecněji. Začněme třeba nevýhodami. – První je samozřejmá: Indikátor neumožňuje přesné kvantitativní měření. (Lze si pomoci výše popsaným připojením multimetru na výstup, ale to je spíše provizorní řešení.) – Další nevýhodou je malý vstupní odpor popsané konstrukce. V uvedených pokusech nevadil, jinak by bylo třeba zvětšit odpor rezistoru spojujícího vstupní svorky. (Mohl by tím ale vzrůst šum.) – V konstrukci je užita jen běžná malá žárovička, změny jejího jasu nemusejí být zřetelně vidět třeba do zadních lavic ve třídě. To by bylo možno řešit použitím výkonnější žárovky (např. automobilové), ovšem znamenalo by to použít výkonnější tranzistor a dobře ho chladit. Použitý typ je už ve stávajícím zapojení za provozu docela horký a nešlo by ho zatěžovat výrazně vyšším proudem. – Indikátor se nedá nikde koupit, musíte si jej zhotovit sami nebo k tomu přemluvit někoho známého (nebo šikovné studenty).
Do stavby indikátoru by se asi neměl pouštět úplný laik, kterému dělá potíže spájet dva dráty pistolovou páječkou (nebo který vůbec neví, co to pistolová páječka je). Na druhé straně z vlastní zkušenosti vím, že obvod TLC272 je velmi vhodnou součástkou k tomu, začít získávat praktické zkušenosti s operačními zesilovači (a děkuji Peterovi Žilavému, že mi tento typ k experimentování před pár lety doporučil). Pro všechny, kdo s ním budou chtít začít pracovat, ještě uvedu rozložení jeho vývodů (při pohledu shora; obvod mějte otočen tak, abyste označení na něm napsané měli čitelné, tj. „hlavou vzhůru“). Ještě jedno skoro samozřejmé doporučení: je vhodné nepájet přímo na „nožičky“ integrovaného obvodu, ale mít jej zasunut v patici.
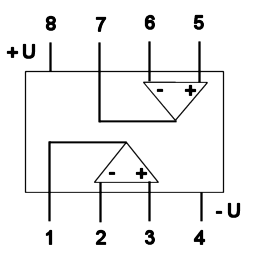
Obr. 3: Rozmístění vývodů obvodu TLC272.
Rozmístění součástek na destičce s pločnými spoji (stačí malý kousek univerzální destičky) zde neuvádím, každý si asi konstrukci přizpůsobí sám.
A teď alespoň několik slov k výhodám:
+ Žárovička jasně a zřetelně indikuje změny napětí. Zvýšení nebo pokles jasu přitom dokážeme sledovat doslova „koutkem oka“ a nemusíme soustřeďovat pozornost na ručku nějakého přístroje neřkuli na digitální displej. + Žárovka změny indikuje podstatně rychleji, než ručka měřicího přístroje. Při běžných školních pokusech s elektromagnetickou indukcí, kdy se k cívce připojuje demonstrační měřidlo, bývá problém v tom, že jeho ručka jen „neochotně“ reaguje na rychlé změny (a při pomalých změnách se zase sotva hýbá). + Pokud se na vstup indikátoru dostane nějaký rušivý střídavý signál (např. 50 Hz indukcí z elektrické sítě) a je zesílen, žárovička bude měnit svůj jas s příslušnou frekvencí. Tak rychlé změny ale naše oči nezaznamenají. Rušivý signál tak na výstupu vlastně nezaznamenáme. + A konečně, jak už bylo naznačeno v úvodu, na celé konstrukci jsou opravdu nejdražším prvkem dvě ploché baterie.
Máte-li mezi svými žáky či studenty nějakého „bastlíře“, třeba si rád pohraje a tento, nebo ještě nějak vylepšený, indikátor vám postaví.
Demonstrace ohybu kolejí za horka
A teď něco pro ty, kdo netíhnou k elektronice. Dále popsaná konstrukce byla inspirována letošní vlnou veder a zprávami o tom, jak se leckde horkem deformují koleje. Fyzikáře (již pokročileji „praštěného“ svou profesí) lehce napadne otázka: Jak by se dala deformace kolejí ukázat ve třídě?
Základní idea je jasná: vzít nějakou kovovou tyčku, na koncích ji pevně zapřít a nahřívat vhodným zdrojem tepla. To by bylo, aby se nezdeformovala!
Skutečnou kolejnici ovšem nemáme šanci ani pevně zapřít, ani pořádně nahřát. Takže něco menšího. Třeba pletací jehlici nebo háček na háčkování. Ty jsou podle váhy zřejmě z hliníku, který má dokonce větší tepelnou roztažnost než ocel, takže deformace by měla být výraznější. Na upevnění konců (zapření) stačí jednoduchá konstrukce ze stavebnice Merkur, která se naštěstí v mnoha domácnostech a snad i školách ještě vyskytuje. Výsledek, jak lze celou věc realizovat, ukazuje obrázek 4.

Obr. 4: Konstrukce pro demonstraci deformace tyče při zahřívání.
Jehlice či háček mají výhodu, že jejich konce dobře zapadnou (opřou se) do dírek v dílech stavebnice Merkur. (V popisované konstrukci byl použit háček o průměru 4,5 mm. Výhodou háčku je skutečnost, že je nesymetrický, takže předem vidíte, na kterou stranu se vyklene. Pletací jehlici by možná bylo dobře před pokusem nepatrně přihnout.) Malé dílky Merkuru s výhodou využijeme jako podložky, jimiž na koncích jehlici či háček „utěsníme“, aby šly do konstrukce zasunout opravdu „nadoraz“. Detail uchycení jednoho konce ukazuje obr. 5.

Obr. 5: Detail uchycení jednoho konce tyčinky (háčku).
Jehlici resp. háček pak stačí nahřát jednou či několika čajovými svíčkami a výrazně se prohne, jak to ukazuje obrázek 6. Realizovaná konstrukce byla tak úzká, že mohla na obalech čajových svíček přímo stát, takže odpadly komplikace s jejím uchycením. Při zahřátí jednou nebo dvěma svíčkami se po vychladnutí jehlice zase narovnala, po zahřátí třemi svíčkami zůstala prohnutá.

Obr. 6. Deformace tyčinky (háčku) po zahřátí. (Před zahříváním byla opravdu téměř rovná.)
Chcete-li, můžete i menší deformace při zahřátí jednou svíčkou zvýraznit pomocí jednoduché přídavné konstrukce také z Merkuru, její popis a fotografie však už necháme do nějaké webové verze tohoto příspěvku.
Trocha teoretických odhadů: o kolik se tyč prohne?
Chcete-li, nemusíte zůstat jen u kvalitativní demonstrace prohnutí tyče. Alespoň přibližně můžeme odhadnout i to, o kolik se tyč (resp. náš háček) prohne do strany.
Spočíst, o kolik by se tyč protáhla do délky, není těžké. Středoškolské tabulky nám sdělí koeficient délkové roztažnosti hliníku: α = 24·10-6. Při zahřátí o 40 stupňů se tedy tyč roztáhne přibližně o tisícinu své délky; háček o délce L=30 cm tedy o ΔL=0,3 mm. O kolik se ale prohne?
Samozřejmě o tolik, aby délka oblouku, který vytvoří, byla L+ ΔL (viz obr.7).
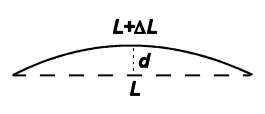
Obr. 7. Pro výpočet prohnutí tyče musíme určit délku oblouku.
Spočíst délku oblouku je už ale úloha spíše pro studenty v úvodním vysokoškolském kurzu, zejména, když si v nějaké učebnici mechaniky (např. Kvasnica a kol.: Mechanika) najdeme příslušný vztah pro tvar oblouku. (Půlka našeho oblouku musí mít tvar jako vetknutý nosník, učebnice nás poučí, že – za zjednodušujících předpokladů vypočtený – tvar takového nosníku v sobě kombinuje parabolu a kubickou parabolu.) Ale kupodivu pro základní představu o tom, jak prohnutí d závisí na prodloužení ΔL, můžeme vyjít z mnohem jednoduššího přiblížení: představit si, že úseky tyče od krajů ke středu jsou úsečky – tak, jak to ukazuje obr. 8.
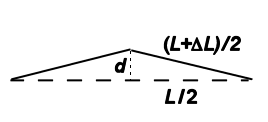
Obr. 8: Přibližně lze prohnutí tyče určit pomocí Pythagorovy věty.
Dále vystačíme s matematikou ani ne středoškolskou. Z Pythagorovy věty plyne 4d2 = (L+ ΔL)2 – L2 a odtud po úpravách přibližně d /L= 0,71·√(ΔL/L) . Naše úvaha se může zdát až příliš hrubá – ovšem zajímavé je, že výpočet vycházející ze skutečného tvaru nosníku dává (pro malá prohnutí) výsledek nepříliš odlišný: d /L= 0,65·√(ΔL/L) . (Podobný výsledek bychom dostali, kdybychom oblouk aproximovali parabolou; koeficient před odmocninou by pak vyšel přibližně 0,61.) Podstatné je, že prohnutí je úměrné odmocnině z prodloužení. Pro výše odhadnuté relativní prodloužení o jednu tisícinu dá odmocnina o něco méně než třicetinu – takže 30 cm dlouhá tyč se prohne asi o 0,6 cm.
Zajímavý by byl i odhad síly, jakou tlačí konce tyče na své opory – ale to už necháme na jindy.
Tak vidíte, jak si lze vyhrát se zařízením za pár korun. (Protože cena, nepočítáme-li díly Merkura, je opravdu mizivá. Čajová svíčka stojí korunu a hliníkový háček, navzdory podivu některých účastnic Veletrhu nápadů byl opravdu zakoupen v létě 2003 za pouhé 2,- Kč.)
Jednoduchý dilatometr
Demonstrovat prodloužení tyče při zahřátí lze rovněž s konstrukcí za pár korun. K následujícímu „měřicímu přístroji“ jsem byl inspirován pokusem předváděným pro účastníky semináře projektu Heuréka (viz http://kdf.mff.cuni.cz/Heureka ). Idea pokusu je však zřejmě letitá a známá (viz obr. 9): Položit konec zahřívané tyče na tenkou osičku (jehlu nebo špendlík), která se může odvalovat po podložce. Posunutí konce tyče se tak převede na otočení – a to ukáže dlouhá ručička připevněná k osičce.

Obr. 9: Princip dilatometru.
Hlavní problém v realizaci konstrukce je aby to celé neprokluzovalo. Tyč (třeba opět pletací jehlice nebo háček) má tendenci po ocelové jehle nekontrolovaně klouzat a podobně je tomu mezi jehlou a podložkou. Dále popsaná konstrukce je vlastně jen jednoduchým „technickým dotažením“ výše popsaného nápadu.
Jak v našem dilatometru zabráníme prokluzování? Velice jednoduše: Na jehlu či špendlík navlékneme kousek bužírky z tenkého izolovaného drátu (vyhoví tenký zvonkový drát). Podložkou budou dvě „kolejničky“ (třeba opět z dílů stavebnice Merkur), aby dotek osičky s podložkou byl „bodový“ (přesněji řečeno „dvoubodový“). Připevnění ručičky je „klasické“: na jehlu napíchneme kousek korku ze zátky, do korku zapíchneme ručičku (třeba z kousku toho zvonkového drátu) a na druhou stranu zátky nezapomeneme zapíchnout dva tři malé hřebíčky pro vyvážení (jinak by nám ručka padala, třecí síla mezi bužírkou a pletací jehlicí přece jen není příliš velká). Celou konstrukci ukazuje obr. 10, detail „převodu na pohyb ručky“ obr. 11.

Obr. 10: Jednoduchý dilatometr.

Obr. 11: Detail osičky dilatometru.
V konkrétní konstrukci byl průměr osičky (špendlíku i s bužírkou) asi 1 mm, délka ručky asi 7 cm. Konec ručky se tedy pohne asi 70-krát víc, než konec tyče. Prodlouží-li se tyč o 0,3 mm (což odpovídá zahřátí asi o 40 K, viz výše), pohne se konec ručky asi o 2 cm. A to už je docela dobře vidět. Sympatické je, že po vychladnutí se ručka vracela (musím přiznat, že až asi na půl milimetru) zase do původní polohy. Možná tedy, že bychom si s tímto dilatometrem mohli troufnout i na nějaká polokvantitativní měření…
Místo závěru
Všem, kdo budete popsané konstrukce zkoušet využít ve výuce, přeji hodně zdaru. A vám, kdo jste (jako já) tak trochu „hračičkové“, přeji hodně radosti při jejich vylepšování a hledání dalších experimentů, v nichž se uplatní. A prosím, dejte mi ty nové nápady, náměty a připomínky vědět…
