Panská fyzika III
Jaroslav Reichl
Pro oživení a zpestření výuky fyziky na střední škole dávám k dispozici několik námětů na pokusy.
1. Trajektorie pohybu, odstředivá síla, vrhy těles, zákon zachování energie, kyvadlo, …
Následující pomůcku vymyslel student Martin Pastrňák (ze třídy 00M) při prezentaci domácích experimentů, které se v mých hodinách staly již tradičním opakováním učiva ve druhém ročníku. Student tímto nápadem demonstroval vodorovný vrh tělesa, nicméně pomůcka má širší využití.
Pomůcky: tenisový míček, síťka od citronů (cibule, …), několik metrů dlouhá stuha
Postup a provedení
Do síťky od citronů či jiného ovoce či zeleniny vložíme tenisový míček a těsně jej do ní zavážeme. Na konec síťky připevníme několik metrů dlouhou stuhu a máme k dispozici pomůcku pro řadu fyzikálních partií (hlavně mechaniku).
Primárně byla tato pomůcka určena pro demonstraci trajektorie vrhů těles v homogenním tíhovém poli Země. Provedení je velmi jednoduché. Stoupneme si před třídu, vezmeme míček do rukou a hodíme v příslušném směru (svisle, vodorovně, šikmo vzhůru, šikmo dolů), přičemž dáváme pozor na to, aby se volná stuha nikde nezachytila. Při pohybu míčku pak stuha krásně „kopíruje“ trajektorii daného pohybu (ve většině uvedených případů část paraboly).
Dalším využitím pomůcky je demonstrace zákona zachování energie. Hodíme-li míček tak, aby se několikrát odrazil od země, je vidět, že maximální výška výstupu mezi jednotlivými odrazy se postupně zmenšuje. Jinými slovy, neplatí zákon zachování mechanické energie, ale obecnější zákon zachování energie (část mechanické energie se přemění na energii vnitřní, práci nutnou k deformaci míčku, …).
S opatrností lze pomůcku použít i k demonstraci odstředivé síly: uchopíme za volný konec stuhy a tenisový míček roztočíme. Ve vhodném okamžiku (kdy nemůžeme nikoho zranit) stuhu pustíme.
Další použití nabízí mechanické kmitání, kdy je možné pomůcku použít jako příklad mechanického oscilátoru, diskutovat, jedná-li se o kyvadlo matematické či nikoliv, hovořit o kmitání tlumeném, netlumeném, nuceném, …
2. Vzájemné působení dvou vodičů s proudem
Ukázat vzájemné silové působení dvou rovnoběžných vodičů, kterými prochází elektrický proud, je spojeno s řadou problémů: aby bylo pozorované přitahování resp. odpuzování vodičů prokazatelné, je třeba vybudit v okolí vodičů velké magnetické pole. To znamená ale i velký proud procházející vodičem, což ne každý vodič vydrží. Tyto obtíže je možné eliminovat použitím dvou proužků alobalu připojenými k akumulátoru. Pro učitele (alespoň pro mě) je poté určitě náročnější na dvourozměrnou tabuli udělat třírozměrný obrázek s vyznačením směru proudu, magnetické indukce a působící síly a „odvodit“ na základě pravidel levé a pravé ruky orientaci působící síly. Z toho důvodu jsem si vyrobil jednoduchou pomůcku, která nemá nic společného s příslušným elektrickým obvodem; slouží jen k názorné ukázce prostorového uspořádání uvažovaných tří vektorů.
Pomůcky: 3 půllitrové PET láhve s uzávěry, 2 laboratorní stojany, kus tvrdšího silnějšího kartonu, 2 špejle, tužka a papír (čtvrtka), lepidlo, několik špendlíků
Postup
Do uzávěrů obou láhví uděláme takový otvor, aby bylo možné láhev uzavřenou uzávěrem nasadit na laboratorní stojan. Z tvrdšího silnějšího kartonu vystřihneme dva kruhy o poloměru zhruba 5 - 7 cm, uprostřed každého z kruhů uděláme takový otvor, aby jej bylo možné těsně nasadit na uzávěr plastové láhve. Pro jistotu je možné zátku do kruhu vlepit lepidlem.
Na čtvrtku papíru, jejíž velikost upravíme tak, aby bylo možné oblepit plastovou láhev, nakreslíme (resp. pomocí tiskárny a počítače vytiskneme) několik výrazných šipek. Na každou láhev pak nalepíme pás se šipkami, přičemž dáváme pozor na to, aby na jedné láhvi byly šipky orientovány opačně než na ostatních (viz obr. 1). Na další 4 proužky čtvrtky nakreslíme po jedné šipce (z didaktických důvodů volíme 2 barvy šipek po dvou kusech). Na dva z uvažovaných proužků (šipky stejné barvy) přiděláme pomocí proužků papíru z rubové strany úchytky pro provlečení špejle. Na dvě špejle pevně přivážeme k jednomu jejich konci špendlík.
Provedení
Na stativové stojany nasadíme příslušné PET láhve (i s uzávěry a připevněnými kartónovými kruhy) podle toho, jestli chceme demonstrovat vzájemné silové působení dvou rovnoběžných vodičů, jimiž prochází proud v souhlasném nebo v opačném směru. Šipky na lahvích představují směr proudu v uvažovaném vodiči. Pomocí pravidla pravé ruky vyvodíme směr magnetické indukce v okolí každého z vodičů a naznačíme jej pomocí proužků se šipkami, které připevníme pomocí špendlíků do kartónu na uzávěru. Potom pomocí Flemingova pravidla levé ruky vyvodíme směr působící síly na příslušný vodič. Směr této síly vyznačíme pomocí špejle, kterou špendlíkem zapíchneme do kartónu a na níž navlékneme proužek papíru se šipkou (viz obr. 2, na kterém je znázorněna situace pro dva vodiče se stejným směrem proudu). Nyní je prostorový model situace dokončený.
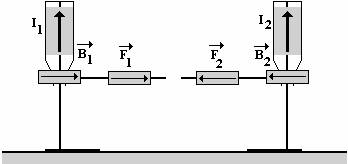
Obr. 1 (vlevo) a 2(vpravo)
3. Měření indexu lomu špendlíkovou metodou
V rámci výkladu optiky jsme s kolegy přemýšleli, jak výuku zatraktivnit pomocí laboratorní práce na téma index lomu. Skleněné půlválce v soupravě pro optiku jsme měli, co nám ale chybělo byly jak zdroje světla, kterými by bylo možné na válec posvítit a sledovat chod paprsků v půlválci, tak příslušné zdroje napětí. Nakonec jsme došli k závěru, že je možné použít tzv. špendlíkovou metodu. Dostupnými prostředky je tak možné určit velmi dobře index lomu daného skleněného půlválce.
Pomůcky: skleněný půlválec (ze souprav pro optiku), několik špendlíků, kartón nebo kus polystyrenu, papír, tužka, pravítko, úhloměr, kalkulačka
Postup a provedení
Na polystyren připíchneme čistý list papíru, na němž jsme předem narýsovali přímku, která bude představovat rozhraní dvou optických prostředí. K tomuto vyznačenému rozhraní opět pomocí špendlíků připevníme skleněný půlválec tak, aby čelo půlválce leželo přesně na vyznačeném rozhraní, které nám celou rovinu papíru nyní dělí na dvě poloroviny: „skleněnou“ a „vzduchovou“. Na papír nyní vyznačíme střed S čela půlválce, do něhož vpíchneme špendlík. Do „vzduchové“ poloroviny vpíchneme další špendlík, uchopíme polystyren do ruky, zavřeme jedno oko a díváme se tak, aby právě vpíchnutý špendlík a špendlík v bodě S ležely v jedné přímce. Třetí špendlík vpíchneme do „skleněné“ poloroviny tak, aby při pohledu přes skleněný půlválec ležel na téže přímce, jako dva již umístěné špendlíky a oko. Na papír si vyznačíme (např. číslem) polohu obou špendlíků (ve „vzduchové“ i „skleněné“ polorovině). Situace je schematicky znázorněná na obr. 3. (Nejedná se o záznam z měření!!!) Postup několikrát opakujeme s různou počáteční polohou prvního špendlíku.
Před vlastním výpočtem sundáme papír z polystyrenu, bodem S vedeme k rozhraní kolmici a vyznačíme dopadající i lomený paprsek (spojíme např. bod 1 ve „vzduchové“ polorovině s bodem S a pak bod S s bodem 1 ve „skleněné“ polorovině). Úhloměrem určíme úhel dopadu a úhel lomu a pomocí Snellova zákonu lomu dopočítáme index lomu skla půlválce (index lomu vzduchu uvažujeme roven 1).
Je možné postupovat i tak, že se „díváme“ ze „skleněné“ poloroviny. To skýtá ale jedno nebezpečí: totální odraz. V určité poloze prvního špendlíku se třetí špendlík při pohledu přes válec již nezobrazí na uvažované přímce.
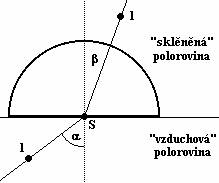
Obr. 3
4. Nepovinný seminář ze třídou 00M
Naše průmyslová škola (Střední průmyslová škola sdělovací techniky, Panská 3, Praha 1) nabízí čtyři studijní obory: digitální a telekomunikační technika, obrazová a zvuková technika - technické zaměření, obrazová a zvuková technika - technologicko organizační zaměření a technické lyceum. Technické lyceum je obor, který slouží jako příprava studentů na studium na vysokých školách technického směru. Studenti mají v učebním plánu v hojné míře zastoupenou matematiku, fyziku, výpočetní techniku, deskriptivní geometrii, CAD systémy a další předměty.
Ačkoliv mají studenti fyziku celé čtyři roky, přesto není v hodinách čas na veškeré dotazy studentů. Proto jsme se se třídou 00M (a souhlasem vedení školy) rozhodli pro středeční seminář, na kterém se studenti (i já) scházeli dobrovolně a řešili jsme problémy, které je aktuálně zajímaly: teorie relativity, kosmologie, černé díry, teorie chaosu, … Kromě těchto teoretických otázek jsme se zabývali i úlohami praktickými: měření rychlosti střely z plynové pistole, tlaková zkouška PET lahví, …, z nichž některé se během školního roku nedařilo dokončit. Ale jejich dokončení plánujeme.
Atmosféru jak na (nepovinném) středečním semináři, tak na (povinných) cvičeních z fyziky, jsem se pokusil zachytit pomocí fotoaparátu.
Miroslav Janáček při střelbě z plynové pistole |
Martin Bak demonstruje existenci odporové síly vzduchu |
Filip Müller, Mirek Janáček, Dan Kloud a Martin Kurčerák studují hračky z Kinder vajíčka. Mirek vše odborně komentuje, neboť referát „Fyzika v Kinder vajíčku“ byl jeho. |
Tak takhle dopadl umělohmotný kbelík a plastová láhev při tlakové zkoušce. Vydržela (podle tlakoměru na pumpičce) 10 atmosfér (1 MPa). |
Detail torza plastové láhve … |
Filip Müller nabíjí vodním kolem blesk od fotoaparátu. Zdařilo, i když Filip musel překonat řadu technických problémů. Mokří jsme byli ale skoro všichni. |
Michal Adamec a Martin Bosák zkouší hrát na poměrně atypickou trubku, kterou objevili ve fyzikálním kabinetu. |
Yesterday, Skákal pes přes oves, Saxana, … to vše zvládl Vašek Potoček zahrát na hudební nástroj vyrobený z prázdných lahví od piva. |
5. Fólie pro zpětný projektor
Nedílnou součástí výuky nejen fyziky jsou zpětné projektory. Možná, že na některých bohatších školách byly nahrazeny již dataprojektory, ale to nic nemění na tom, s čím se chci s vámi podělit. Připravil jsem si řadu fólií, které používám při výuce. Pravda je, že některé byly vyrobeny speciálně pro předmět Technická fyzika, který učím u nás ve škole, ale dají se použít i na běžných hodinách fyziky resp. na seminářích či kroužcích. Jedná se o fólie různých technických zařízení (např. fotoaparát, filmová kamera, videokamera, …), grafy (např. graf závislosti hlasitosti na frekvenci, směrová charakteristika mikrofonů, …), srovnávací tabulky, …
A nejen to. Inspirován polskými kolegy z minulých Veletrhů nápadů učitelů fyziky začal jsem si dělat i fólie historické, abych jednak sám sobě a jednak studentům ukázal „historické souvislosti“ - kdo žil v době Newtonově, jaká díla se tvořila,… Zkusil jsem to ve školním roce 2001/2002 na prvácích (a částečně druhácích) a docela to mělo úspěch. Když si k tomu vynajdete i hudbu z dané doby, můžete vykládat Newtonovy pohybové zákony a v pozadí mohou znít díla Antonia Vivaldiho, Johanna Sebastiana Bacha, Georga Friedricha Händela, … Když tyto fólie viděli kolegové, co učí český jazyk nebo dějepis, málem se psali do pořadí, kdo si co kdy půjčí.
Fólie jsem „vyráběl“ tak, že jsem si příslušný obrázek naskenoval do počítače (většinou z populárních nebo starších knih, takže obrázky byly tu na žlutém, tu na modrém pozadí, na časem zažloutlém pozadí, …), upravil (aby byly všechny na pozadí bílém) a vytiskl na fólie. Všechny obrázky, které mám na fóliích, mám též v elektronické podobě. Pokud bude zájem, můžete se na mě obrátit s tím, že napíšete, co potřebujete a já vám obrázek pošlu v elektronické podobě. Přenos obrázku na fólii si už budete muset zařídit sami …
Několik ukázek (uvádím ty obrázky, které jsou malé a na kterých bude při malém formátu brožury vůbec něco vidět) je připojeno na konci příspěvku.
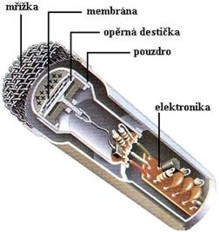
Elektrostatický mikrofon |
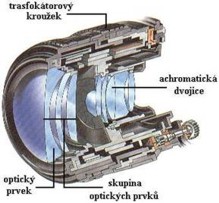
Transfokátor |
Isaac Newton (25. 12. 1642 - 20. 3. 1727) |
Antonio Vivaldi (4. 3. 1678 - 28. 7. 1741) |
Goya: Oblečená Maja |
|