Kroužek fyziky pro středoškolské studenty
Miroslav Jílek
V příspěvku popisuji několik pokusů a námětů na práci se studenty, které vznikly při přípravě kroužku fyziky konaného v školním roce 2001/2002 na MFF UK v Praze. Cílem kroužku bylo pomocí rozboru jednoduchých pokusů společně se středoškolskými studenty hlouběji prozkoumat některé fyzikální jevy a jejich praktické aplikace. Věnovali jsme se také řešení problémů a úloh, na které při běžné výuce nezbývá čas. V současné době pracujeme na zpracování programu kroužků do elektronické podoby, aby mohly sloužit jako možné náměty pro práci se studenty v různých seminářích a rozšířených hodinách fyziky, ale i při běžné výuce na školách.
Jedním z velkých témat, kterým jsme se zabývali, byly srážky různých těles a jejich souvislost se zákony zachování hybnosti a energie. K přiblížení tohoto tématu můžeme uvést úlohu:
Co se stane s loďkou, jestliže si za bezvětří stoupneme na její záď a budeme foukat do plachet, případně místo svého dechu použijeme výkonný ventilátor? Může se rozjet? Dopředu nebo dozadu? Nebo zůstane stát?
K praktickému vyzkoušení této situace jsme si vytvořili jednoduchý model loďky z víka dózy od jogurtů. Stožár pro malou papírovou plachtu jsme vyrobili z tvrdého izolovaného drátu, který jsme izolepou přilepili na přední část víka (loďky), viz obr.1. Jako zdroj vzduchu jsme použili nafukovací balónek s kouskem trubičky z propisovačky ke směrování proudu vzduchu. Trubičku s balónkem jsme pomocí pružných plíšků připevnili k dřevěnému špalíku a ten jsme přilepili na loďku tak, aby trubička směřovala na plachtu. Loďku s nafouknutým balónkem jsme vypouštěli na hladině vody ve vaničce.
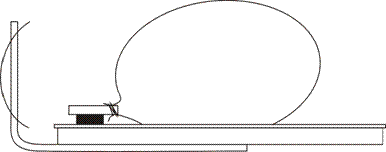
Obr. 1
Výsledkem pokusu je, že se loďka rozjede dopředu. To můžeme vysvětlit z hlediska zákona zachování hybnosti. Celková hybnost loďky s nafouknutým balónkem před je na začátku nulová. Můžeme-li považovat srážku vypouštěného vzduchu s plachtou za pružnou, odráží se vzduch od plachty směrem dozadu, a tedy vektor hybnosti každé malé části tohoto vzduchu míří dozadu. Protože má být zachována původní nulová hybnost loďky se vzduchem, znamená to, že vektor hybnosti samotné loďky míří dopředu.
Jestliže pokus opakujeme s loďkou bez plachty, rozjede se loďka ze stejného důvodu dozadu. To je intuitivně mnohem lépe pochopitelný případ klasického reaktivního pohonu. Protože odraz vzduchu od plachty není ideálně pružný a proud vzduchu nemusí dopadat na celou plachtu, můžeme vhodnou kombinací velikosti a vzdálenosti plachty od zdroje vzduchu dosáhnout toho, že loďka zůstane stát na místě.
Jiným příkladem srážky dvou těles je dopad roztočeného (například volejbalového) míče na zem. Otázka je: Jaký bude směr rotace míče po odrazu od země?
Jednoduchým pokusem se můžeme přesvědčit o tom, že při dopadu míče z větší výšky je směr rotace po odrazu opačný než před dopadem. Při dopadu z malé výšky s dostatečně velkou rotací je tento směr stejný jako před dopadem. Při dopadu z větší výšky je totiž míč během srážky více deformován, samotný kontakt se zemí trvá déle a to stačí k tomu, aby se míč zastavil a při odpružení byl reaktivní silou roztočen na druhou stranu. Při dopadu z malé výšky se míč během srážky nestačí zcela zastavit a pouze se zpomalí. Volbou vhodné výšky dosáhneme i toho, že se míč právě zastaví a po odrazu nerotuje.
V technické literatuře se můžeme dočíst, že tohoto jevu se využívá například při přistávání letadel, kdy se kola letadla roztáčejí ještě před přistáním, aby se jejich samovolným roztočením při prvním kontaktu se zemí nezvětšoval moment hybnosti letadla, který by jej sklápěl na příď.
Dalším velkým tématem, kterému jsme se věnovali, byly rotace těles. K přiblížení ve škole málo diskutovanému pojmu Coriolisovy síly můžeme například využít jednoho z následujících pokusů.
U prvního pokusu sledujeme dráhu kovové kuličky pohybující se po desce, která se otáčí. Libovolnou dřevěnou (nejlépe kruhovou) desku, v našem případě například momentový kotouč, umístíme na podložku s čepem, na starý magnetofon nebo na libovolnou jinou točnu tak, aby s ní bylo možno otáčet. K desce připevníme jednoduchý prak ze slabé kloboukové gumy a kousku tvrdého papíru nebo kůže, který bude kuličku vystřelovat (malou rychlostí) směrem od obvodu ke středu desky.
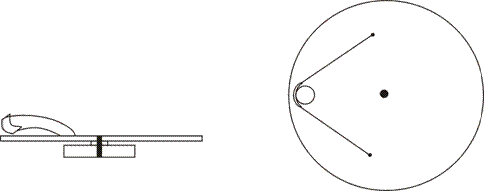
Obr. 2
Dráhu kuličky znázorníme tak, že na desku položíme papír, který překryjeme kopírovacím papírem, takže kulička pohybující se po kopírovacím papíru otiskne svoji trajektorii na papír.
Vypustíme-li kuličku z praku bez současného otáčení deskou, bude se pohybovat směrem ke středu a vykreslí na papíře rovnou čáru. Jestliže provedeme stejný pokus za současného otáčení deskou, bude na kuličku v systému otáčející se desky působit Coriolisova síla, která způsobí zakřivení trajektorie kuličky vůči desce do strany. Na papíře můžeme sledovat toto zakřivení a jeho závislost na směru a rychlosti otáčení desky.
Dalším způsobem, jak pozorovat účinky Coriolisovy síly, jednak z hlediska pozorovatele v otáčející se soustavě, jednak z hlediska venkovního pozorovatele, je využití točící se židle. Můžeme si vyrobit jednoduchý prak z přibližně 60 cm dlouhé dřevěné latě, kloboukové gumy a kousku tvrdého papíru nebo kůže tak, že lať tvoří vodicí lištu pro projektil, kterým je pingpongový míček, viz obr. 3.
Posadíme se na židli, natažený prak (guma samozřejmě není příliš silná) namíříme kolmo k ose židle například proti svému čelu, roztočíme se a uvolníme pingpongový míček. Na ten působí v otáčejícím se systému židle Coriolisova síla, která způsobí zakřivení jeho trajektorie, takže nás míček mine. Pokud se s židlí nebudeme točit, míček nás samozřejmě zasáhne, což vzhledem k použitým prostředkům není nijak nebezpečné.

Obr. 3
Židli můžeme využít ještě jiným způsobem, chceme-li účinek Coriolisovy síly přímo cítit. Posadíme se na židli a uvolněnou rukou si nacvičíme rychlý pohyb od kolen směrem ke svému čelu. Jestliže se na nacvičený pohyb nebudeme soustředit a provedeme ho současně s rychlým otáčením na židli, ucítíme, jak na ruku během pohybu působí Coriolisova síla, která ji odkloní tak, že mine naši hlavu.
Při výkladu rotace těles se často uvádějí známé pokusy se setrvačníky. Vysvětlení chování roztočeného setrvačníku, působíme-li na něj vnější silou, vyžaduje poměrně složitý rozbor situace, na který v tomto příspěvku není prostor.
Můžeme si však všimnout, že takové chování se projevuje i ve zcela běžných situacích. Pustíme-li například minci tak, aby se skutálela po mírně nakloněné rovině, můžeme pozorovat její zajímavý pohyb. I když ji nevypustíme zcela kolmo k podložce, a zdálo by se tedy, že musí spadnout na stranu, stočí se ve směru pohybu tak, že se vlivem setrvačnosti ve směru pohybu překlopí částečně na druhou stranu. Tento jev se pak opakuje, mince se překlápí čím dál méně z jedné strany na druhou, až se postupně vyrovná. Stejný efekt usnadňuje například jízdu na kole nebo na motocyklu.
Pohyb typický pro setrvačník můžeme také spolu s dalšími jevy pozorovat při letu bumerangu. Jestliže se správně vržený bumerang vrátí zpět k nám, znamená to, že během svého letu vykoná jednu precesní otáčku.
Jednoduchý model bumerangu vhodný pro pozorování jeho letu ve třídě je možné vystřihnout podle obr. 4 (průměr bumerangu je přibližně 12 cm) z tvrdého kartónu (například ze zadních desek poznámkového bloku). Ramena bumerangu je potřeba vrtulovitě nakroutit na jednu nebo druhou stranu podle toho, na kterou stranu ho budeme roztáčet. Bumerang je pak třeba kvůli stabilitě rotace vypouštět tak, že ho položíme na rovnou podložku (například sešit), kterou držíme v jedné ruce před sebou a do jednoho ramene přečnívajícího přes podložku udeřit tužkou. Roztočený bumerang opustí podložku a při správném poměru rychlosti rotace a rychlosti vlastního pohybu opíše charakteristickou trajektorii a vrátí se zpět.
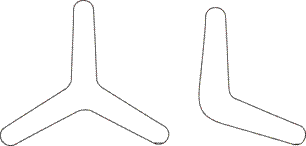
Obr. 4
Poslední pokus, který bych rád zmínil, je jednoduchý, efektní model výbušného motoru, na kterém je možné pozorovat různé druhy energetických přeměn. Model vytvoříme z kousku prkénka, krabičky od fotografického filmu a elektrického zapalovače plynu na baterii, který lze levně koupit na tržnici.
Ve víčku krabičky propíchneme dvě dírky a protáhneme jimi těsně dva drátky, jejichž konce odizolujeme v délce asi 0,5 cm. Konce drátků zahneme proti sobě tak, aby mezi nimi zůstala 3 – 5 mm široká mezera. Víčko přibijeme dvěma hřebíčky k prkénku rantlem nahoru tak, že krabičku je možné do víčku zasadit a ohnuté konce drátků jsou uvnitř krabičky. Zapalovač rozšroubujeme a vyvedeme z něj dva drátky, které jsou spojeny s jiskřištěm. Ty spojíme s drátky vedoucími z krabičky a model je hotov, viz obr. 5.
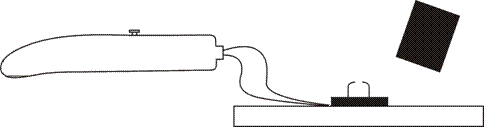
Obr. 5
Krabičku naplníme několika kapkami lihu, zacvakneme ji do víčka a necháme líh chvilku odpařit. Sepneme zapalovač, jiskra uvnitř krabičky zapálí lihové páry a krabička se silným bouchnutím vyletí asi 5 m vysoko. Pokud se páry nezapálí, znamená to většinou, že páry jsou přesycené, v tom případě je třeba přebytek lihu vylít a krabičku profouknutím okysličit, nebo je krabička příliš studená a je potřeba zahřát ji v ruce. Krabičku lze místo plynovým zapalovačem zapálit také například pomocí indukční elektriky nebo jiného zdroje vysokého napětí.
Pokud chceme změřit velikost energie, která se během výbuchu přemění na kinetickou energii krabičky, můžeme krabičku zatížit například kouskem plastelíny, zvážit ji a energii spočítat z výšky do které krabička vyletí. V našem případě vyšla tato energie přibližně 0,6 J. Vzhledem k tomu že spalné teplo 1 mm3 lihu je asi 23 J, můžeme posoudit, jak malá je účinnost takto jednoduchého zařízení.
Na závěr bych chtěl poznamenat, že během mého vystoupení samozřejmě nebylo zdaleka možné předvést všechny náměty, které se během ročního fungování kroužku fyziky podařilo shromáždit. Podrobné informace o programu kroužků spolu s vysvětlenými pokusy a řešenými úlohami budou po zpracování dostupné například na webových stránkách: http://fyzweb.cuni.cz.
