Pokus o kvantitativní interpretaci jednoho hydrodynamického paradoxu

Pavel Konečný

Cílem této práce bylo připravit pokus demonstrující jeden z hydrodynamických paradoxů založených na Bernoulliově rovnici a jeho elementární interpretaci spolu s kvantitativním měřením. Tento jev nebývá v učebnicích běžně uváděn. Jeho elementární výklad (odpovídající středoškolské úrovni) však dovoluje vyslovit také kvantitativní předpověď, kterou lze v jistém smyslu experimentálně ověřit. K přípravě experimentu je zapotřebí zručnost na úrovni leteckého modelářství, finanční náročnost je přiměřená.

K předvedení paradoxu potřebujeme kromě vhodné tenkostěnné trubičky s lemem (osvědčila se hliníková tuba od šumivého celaskonu s odříznutým dnem) regulovatelný generátor vzduchu s parametry na úrovni průměrného vysavače, PVC kanalizační tvarovku typu „koleno“ vhodného průměru a běžný dílenský materiál. Náročnější na zhotovení je pouze nátrubek, ve kterém by se tenkostěnná trubička mohla pohybovat volně, ale přitom relativně bez vůle. Lze jej zhotovit například navinutím hnědé (mokré) lepící pásky přes separační fólii (zajišťující potřebnou vůli) přímo na vybranou trubičku. Paradox vyplyne z porovnání jevů, které nastanou ve dvou různých případech.

1. Nátrubek připojíme na výstup generátoru (kolmo nebo šikmo vzhůru). Vzduch je vyfukován přes nátrubek a vsunutou trubkou ven do atmosféry.

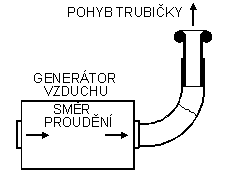
2. Nátrubek připojíme k sání generátoru (opět šikmo nebo kolmo vzhůru). Vzduch je naopak přes trubičku z okolní klidné atmosféry nasáván.

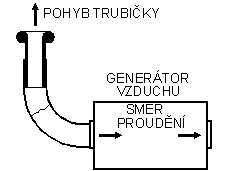
V situaci dle bodu 1. bude trubička dostatečně silným proudem vzduchu vyfouknuta z nátrubku ven. Příčinou jsou síly viskózního tření, které působí ve směru proudění. Proto lze v situaci dle bodu 2. nejspíš očekávat pohyb trubky hlouběji do nátrubku (není-li ovšem na mechanickém dorazu). Experiment však ukáže opak. Trubička je opět vystřelena. Tentokrát proti proudu vzduchu.

Elementarizovaný výklad vychází z představy („ideálního“) tryskového motoru ve tvaru trubky se zanedbatelnou tloušťkou stěny s průřezem o plošném obsahu S, na sací straně opatřené lemem a ve střední části dmychadlem. Předpokládáme, že dmychadlo uděluje v celém průřezu trubky čerpané ideální nestlačitelné tekutině o hustotě ρ konstantní rychlost o velikosti v („ideální“dmychadlo). Předpokládejme dále, že motor je vůči ideální tekutině v klidu a že trubka motoru je natolik dlouhá, aby byl vyloučen vzájemný vliv vstupu a výstupu.

Spočítejme elementárním způsobem statický tah F_stat1. tohoto systému. Za uvedených předpokladů urychlí „ideální“ dmychadlo za časový interval Δt ideální tekutinu o hmotnosti Δm = SρvΔt na rychlost o velikosti v a udělí ji tedy hybnost o velikosti Δf = Sρv²Δt. Statický tah motoru je tedy roven

F_stat1. = S ρ v²

Součtem tlakových sil působících po celém (vnitřním i vnějším) povrchu motoru včetně dmychadla určíme statický tah F_stat2. Vzhledem k symetrii problému jsou tlakové síly působící na vnější i vnitřní povrch válcové části vzájemně kompenzovány. Nenulovou složku ve směru osy motoru mají pouze tlakové síly působící na lem a „ideální“ dmychadlo. Velikost jejich výslednice označme F_lem a F_dmych.

Je-li v velikost rychlosti proudění v trubce motoru, je tlakový spád Δp na dmychadle roven Δp = ½ρv². (Za dmychadlem je vzhledem ke geometrii problému a idealizovaného zadání stejný tlak jako v okolní klidné ideální tekutině.) Velikost výslednice tlakových sil působících na „ideální“ dmychadlo je pak F_dmych = ½ Sρv² Musí platit, že

F_stat1. = F_stat2. = F_lem + F_dmych = S ρ v²

a pro velikost F_lem výslednice tlakových sil působících na lem tedy máme

F_lem = ½ ρv².

Za uvedených předpokladů je tedy možné určit výslednici tlakových sil působících na lem trubičky, která saje (ideální) tekutinu, aniž by bylo nutné řešit rovnice proudění.

Poznámka: Kvalitativní výklad je možné odvíjet například od toho, jaké jsou důsledky tvaru proudnic v okolí sacího otvoru. Směr proudění v blízkosti ústí trubky lze demonstrovat pomocí špejle s bavlnkou.

Pokus o experimentální ověření je založen na následující konstrukci (viz. obr):

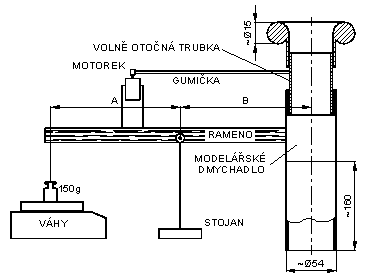
Základním prvkem tryskového motoru je modelářské dmychadlo (cca 600 Kč). Použitý typ má následující parametry: maximální krátkodobý tah 630 mN při napájení 7.2 V a 3 A. Vlastní hmotnost dmychadla 30 g., vnější průměr 52 mm.

Výfukové a sací trubky jsou zhotoveny navinutím hnědé lepící pásky (papír s vrstvou klihu) na vhodný trn, průměrem vyhovuje hliníková plechovka od limonády o průměru 53 mm. Jako separační a potřebnou vůli vymezující vrstva slouží jedna nebo dvě vrstvy fólie do meotaru. Lem je zhotoven ze stavební PUR pěny vypěněním do formy. Tíha nátrubku s lemem by měla být menší než 1/2 maximálního tahu motoru. V popsaném provedení měl nátrubek hmotnost 7.7 g.

Motor je upevněn na dvojzvratné páce zhotovené z dřevěného modelářského nosníku 5x21 mm s ramenem délky 440 mm. Páka je upevněna pomocí dvou kuličkových ložisek malého průměru s osou v horizontální rovině. V základní poloze je motor orientován nátrubkem svisle vzhůru a rameno páky horizontálně. V této poloze je rameno stabilizováno šňůrkou přivázanou k závaží o hmotnosti cca 150g umístěném na misce digitální váhy. Dvojzvratnou páku je nutno podle potřeby na straně motoru dovážit tak, aby při provozním výkonu dmychadla tah motoru rameno nezvedal. (Ve vyzkoušeném uspořádání odpovídala nerovnováha maximálnímu měřitelnému tahu cca 620 mN).

Vstupní nátrubek s lemem je volně nasazen na tenkostěnnou hliníkovou trubku (z hliníkové plechovky od nápoje). Aby nedocházelo k váznutí, trubka vykonává pomocí náhonu (gumičkou od elektromotorku viz obr. 3) nucený střídavý rotační pohyb. Motorek je napájen z generátoru funkcí střídavým signálem o frekvenci kolem 1 Hz. Otáčivé zrychlení musí být takové, aby se nátrubek s lemem setrvačností protáčel.

Popis experimentu:

Při sejmutém vstupním nátrubku vynulujeme váhy. Pak odečteme údaj vah s nasazeným nátrubkem. Poměr tohoto údaje ku hmotnosti nátrubku představuje korekční faktor na nerovnoramennost páky. Uvedeme do chodu dmychadlo a zapneme motorek nuceného střídavého rotačního pohybu. Postupným zvyšováním napětí nastavíme právě takový výkon dmychadla, aby se nátrubek volně vznášel nad dolním dorazem, neklesal a nestoupal. Za předpokladu, že síly smykového tření nijak významně tento stav neovlivňují, vztlakové síly působící na nátrubek právě vykompenzovaly tíhovou sílu, která spolu se silami aerodynamického odporu působí na nátrubek ve směru opačném (motor je orientován svisle). Čtený údaj na vahách je pak úměrný té části tahu motoru F_dmych exp, která dle ideálního modelu odpovídá výslednici tlakových sil působících na dmychadlo. Tah na vstupním nátrubku s lemem F_lem exp je úměrný údaji vah při vypnutém dmychadlu a s nasazeným nátrubkem. Poměr obou údajů dle ideálního modelu odpovídá poměru F_lem/F_dmych = 1. Ve výše uvedeném experimentálním uspořádání bylo dosaženo hodnoty F_lem exp/F_dmych exp = 0,82.

Poznámka: Indikátorem správnosti funkce zařízení je míra citlivosti, s jakou nátrubek reaguje na změnu výkonu dmychadla.

Aerodynamika experimentu je poměrně komplikovaná a její diskuse se vymyká zvolené úrovni výkladu i rozsahu příspěvku. Komplikovaný je například vliv tvaru a rozměru lemu. V pokusech s reálnou tekutinou jsou vždy přítomny nejen síly tlakové, ale i síly k povrchu tečné. Provedení motoru a vlastnosti dmychadla také nemohou plně odpovídat předpokladům. Nelze tedy jednoznačně přiřadit naměřené F_dmych exp a F_lem exp jen dmychadlu nebo lemu nátrubku.

Je však možné zdůvodnit, proč   musí být poměr F_lem/F_dmych v reálném experimentu menší jak jedna. Aerodynamický odpor v sací části způsobuje dissipaci energie. Na dmychadle musí být tedy pro dosažení stejného hmotnostního průtoku reálné tekutiny větší tlakový spád, než by byl v případě ideální tekutiny. (Dmychadlem je zde třeba rozumět spíš celý zbytek systému bez pohyblivého nátrubku.) Naměřená hodnota F_dmych exp bude tedy vyšší. Naopak, na nátrubek působí odporové síly, jejichž výslednice má opačný směr, než vztlak na lemu nátrubku. Naměřená hodnota F_lem exp bude tedy nižší. Tento posuv v poměru sil je však zapříčiněn interakcemi uvnitř systému a nemá vliv na tah motoru jako celku.

Popsaný experiment rozhodně nelze považovat za měření parametrů aerodynamického jevu, ale jako problém pro experimentální práci žáků či studentů v oblasti základů mechaniky tekutin, domnívám se, může sehrát užitečnou roli.