Pár věcí z tábora 5 – tentokrát o energii
Leoš Dvořák
Tento příspěvek volně navazuje na sérii příspěvků v minulých ročnících Veletrhu nápadů, ([1] – [4]) popisujících některé náměty z Letních matematicko-fyzikálních táborů pro středoškoláky a z jarních neformálních soustředění pro posluchače studia učitelství na Malé Hraštici. Tentokrát uvádí několik nápadů na jednoduché experimenty týkající se energie a jejích přeměn.
Určujeme solární konstantu
Jak si přečteme v řadě učebnic, ze Slunce přichází na naši Zemi za 1s energie asi 1,37 kJ na každý 1 m2 plochy postavené kolmo ke slunečním paprskům. Tato hodnota (1,37 kW/m2) bývá označována jako solární konstanta. Část energie odrazí a rozptýlí již atmosféra, takže na zemském povrchu činí tok energie ze Slunce zhruba 1 kW/m2. Pokud plocha, na niž záření dopadá, není kolmá ke slunečním paprskům, dopadá na 1 m2 samozřejmě méně energie: uvedený 1 kW musíme násobit cos α, kde α je úhel, který svírá kolmice k ploše se směrem paprsků. Jak se přesvědčit, že tolik energie skutečně na Zem dopadá?
První možnost: miska s vodou
Jednoduchou možností je udělat si něco jako malý „sluneční kolektor“. Stačí třeba plochá mistička z pěnového polystyrénu (ta bude dobře izolovat teplo) vyložená černou fólií, jaká se prodává v potřebách pro zahrádkáře. Do mističky nalijeme trochu vody, postavíme za jasného letního dne na slunce (tedy na místo, kam dopadají sluneční paprsky) a měříme postupně stoupající teplotu vody. K měření lze s výhodou užít např. malý multimetr DT830C, který má sondu pro měření teploty.
Pozn.: Přesnost měření teploty daným multimetrem je 1 stupeň. Při měření dejte pozor, aby se multimetr sám na slunci příliš nezahřál. Je-li sám zahřátý na 40 a více stupňů Celsia, měří teplotu již s chybou několika stupňů. Jinak jde ale o užitečný přístroj, který navíc v letošním roce zlevnil na cenu kolem 250 Kč.
Jsou-li rozměry mističky asi 15 x 15 cm, bude průmět plochy kolmo ke slunečním paprskům (v našich zeměpisných šířkách v době kolem letního slunovratu kolem poledne) asi 200 cm2, takže výkon slunečního záření dopadajícího do mističky bude asi 20 W. S varnou konvicí to soupeřit nemůže, ale k měření to postačí. Tmavá fólie většinu záření pohltí, od ní se ohřeje voda – za 1 minutu by tedy měla přijmout teplo asi 1,2 kJ, tedy necelých 300 kalorií. Nalijeme-li do mističky 0,2 l vody, měla by její teplota díky slunečnímu záření stoupat každou minutu o asi 1 a půl stupně Celsia.
V naší jednoduché konstrukci není povrch vody nijak zakryt, takže při vyšších teplotách vody výrazně rostou ztráty tepla. Měření má proto smysl provádět, jen dokud teplota vody nestoupne o několik stupňů nad teplotu okolí. V autorem realizované konstrukci stoupala teplota asi o 1 stupeň za minutu. Výpočet solární konstanty pak dal něco přes 700 W/m2. Výsledek není nejpřesnější, ale jednoduše nás (a žáky) přesvědčí, že na metr čtvereční skutečně od Slunce dopadá mnoho set wattů.
Uvedeným „zařízením“ lze ohřát vodu dokonce i při mírně zatažené obloze a i mimo vrcholné léto. Na začátku května při teplotě vzduchu 17°C a bez přímého slunečního svitu se voda ohřála až na 25 °C. K zamezení ztrát tepla je v tomto případě vhodné přikrýt mističku průhlednou potravinářskou fólií. Ovšem jednoduchá řešení mají své meze: pokusíme-li se za slunečního svitu takto ohřívat vodu na vyšší teplotu, orosí se fólie ze spodní strany a „stíní“. Je vidět, že daná konstrukce dává mnoho příležitostí k vylepšení a může být námětem pro malé projekty žáků a studentů.
Druhá možnost: vařit kapku vody čočkou
Druhý způsob dává ještě mnohem méně přesné výsledky a může spíše sloužit ke kvalitativní demonstraci toho, co sluneční energie dokáže. Soustředíme prostě sluneční světlo lupou na malou kapku vody, ta se za chvíli začne vařit a pak se vypaří docela.
Teoretický odhad: Lupa o průměru 5 cm má plochu necelých 20 cm2, soustředí tedy sluneční záření o výkonu asi 2 W. Kapku vody na podložce můžeme brát jako polokouli o průměru řekněme 3 mm. Její hmotnost vychází necelých 5 mg. K ohřátí takové kapky o 1 °C stačí energie 0,02 J (k ohřátí o 80 °C tedy necelé 2 J) a k vypaření asi 10 J. Uvedenou čočkou bychom tedy měli za několik sekund kapku zahřát z pokojové teploty na bod varu a zcela vypařit.
Ve skutečnosti se ovšem ohniskem lupy budeme jen těžko strefovat do kapky, voda navíc pohltí jen část energie, v celém experimentu jsou značné ztráty…
Prakticky to znamená: Použijte raději větší lupu, vodu nějak „začerněte“ (např. tuší), a za zhruba půlminutu až minutu kapku opravdu vypaříte. Solární konstantu z tohoto experimentu raději odhadovat nebudeme, stěží by nám vyšla přes 200 W. I když – vynalézavosti se meze nekladou. Zkuste pokus zdokonalit, třeba vám bude vycházet lépe. Ještě dvě praktické rady: Podložka by neměla odvádět moc tepla. Osvědčil se kousek plastelíny. Druhá rada: Dívat se nechráněnýma očima na kapku v ohnisku je velmi nepříjemné a na kvalitě zraku nám to asi nepřidá. Sledujte ohnisko přes začerněné sklo. Ještě lepší je filtr pro svářeče – černě vypadající sklíčko, které lze koupit asi za 40 Kč. Chtějte filtr s co nejnižším číslem, 8 je pro daný pokus optimální, filtrem č.10 už není vidět skoro nic, ten je spíš pro sledování zatmění Slunce. Filtry s číslem menším než 7 se prý nevyrábějí.
Sluneční „pec“
Na konstrukci „sluneční pece“ pracovali na hraštickém soustředění Jan Koupil a Václav Skřivan; na letním táboře pro středoškoláky konstruovali pod vedením Miroslava Jílka vylepšenou „pec“ Kamil Daněk a Kamil Al Jamal. Princip je jednoduchý: Zrcátka o rozměrech asi 5 x 10 až 10 x 15 cm umístíme v řadě na asi 1 až 1,5 m dlouhé prkénko tak, abychom je mohli natáčet. (Zrcátka jsou kolmo na prkénko.) Osvědčilo se nalepit každé zrcátko na dřevěný hranolek, v němž je vyvrtána díra rovnoběžná s rovinou zrcátka. Touto dírou nasadíme hranolek se zrcátkem na hřebík procházející prkénkem. Zrcátka pak natočíme tak, aby odrážela sluneční světlo do společného ohniska. V něm umístíme např. začerněný plech, který bude slunečními paprsky ohříván.

Řad zrcátek by mohlo být víc, ale jedna (s celkovou plochou přes 0,1 m2) postačí. Do ohniska soustředí sluneční záření s výkonem zhruba 100 W. Při závěrečném předvádění na letním táboře (v konstrukci se dvěma řadami zrcátek) bylo ráno po osmé hodině dosaženo teploty až 200°C. To už stačí na usmažení vajíčka.
Pokud do ohniska umístíme plech s připevněnou tenkou trubičkou, do níž budeme přivádět vodu, můžeme dosáhnout toho, že z druhého konce trubičky fouká pára. (Na této části projektu pracoval na táboře Vít Zajac.)
Katapult aneb o energii v mechanice
Potenciální a kinetická energie a jejich přeměny patří ke „klasickým“ a možná někdy trochu nudným partiím klasické mechaniky. Ale zkuste navrhnout a postavit katapult, v němž by pokles těžkého závaží vymrštil co nejdál menší „střelu“ – například dřevěný hranolek, kámen nebo sáček s vodou.
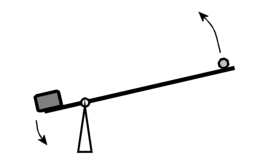
Na první pohled je to jednoduché: Katapult je v podstatě dvojzvratná páka, na jejímž kratším rameni klesá závaží, a delší rameno urychluje střelu. Ale jak dlouhá udělat ramena, aby katapult dostřelil co nejdál? Stačí pro zvyšování dostřelu volit co nejtěžší závaží? Zdánlivě jednoduchý úkol při bližším pohledu přináší řadu zajímavých problémů a může být inspirací jak pro teoretické úvahy a příklady, tak pro praktické projekty.
Na Hraštici řešili a stavěli menší katapult Pavel Böhm, Pavel Kovář a Jakub Jermář, na letním táboře stavěli větší katapult pod vedením Jaromíra Kekuleho Radek Šachl a Richard Gracla.
Z mechaniky se na hraštickém soustředění objevilo ještě více zajímavých problémů, které by mohly oživit výuku fyziky. Jeden za všechny: Jak velkou energii má prst, jímž cvrnkáme do kamínku nebo kuličky? (Rychlost by šla změřit, ale přece si neusekneme prst, abychom ho zvážili a změřili jeho moment setrvačnosti…) A jakou energii má ruka, když praštíme do stolu?
Hrátky s elektromotorky
V prodejnách elektrosoučástek (a asi i dalších) lze občas za cenu kolem 15 Kč sehnat malé elektromotorky fungující na plochou baterii. Podobné by šly „vykutat“ i z řady starých hraček. Motorky však nemusíme užívat jen k převodu elektrické energie na mechanickou, ale i obráceně – jako dynama.
Samozřejmě bychom je mohli využít i ke kvantitativním měřením a zjišťovat třeba účinnost. Lze je však použít i pro jednodušší „hrátky a hříčky“ (které možná v hlavách žáků nezaměřených speciálně na fyziku mají šanci spíš utkvět). Uveďme náměty na tři takové hříčky:
První můžeme vznešeně nazvat „bezdrátový přenos energie“. Energii mezi dvěma motorky, z nichž jeden bude fungovat jako dynamo, přeneseme opravdu bez drátu: špejlí. Pomocí tenké bužírky spojíme konce špejle s osičkami elektromotorů, jeden motorek napájíme z ploché baterie, k druhému připojíme třeba svítivou diodu. Špejle se točí, energie je přenášena a dioda svítí.
Druhou hříčkou je akumulace energie. Ne ovšem v akumulátoru, to by bylo příliš jednoduché. Ale v obyčejné prádelní gumě!
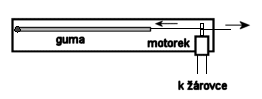
Motorek připevníme na jeden konec dřevěné latě tak, aby jeho osička bylo kolmo na delší stranu latě. Ke druhému konci latě připevníme hřebíčkem konec gumy (kratší než lať). Na druhý konec gumy navážeme režnou nit nebo tenký silonový vlasec. Nit natáhneme k osičce motorku, obtočíme ji kolem ní a volný konec si necháme v ruce. Když za nit zatáhneme, natahujeme gumu a současně otáčíme osičkou motorku. (Pozn.: Na osičku je třeba předem těsně nasadit tenkou bužírku, aby nit neprokluzovala. Je též vhodné osičku prodloužit, např. hřebíkem nebo hřídelkou z Merkuru.)
Když táhneme za nit, guma se natahuje – a ukládá se do ní energie. Když nit povolíme, guma ji táhne zpět a nit otáčí hřídelkou motorku. Ten funguje jako dynamo a dokáže rozsvítit i připojenou žárovičku. Akumulovaná energie koná práci, žárovka svítí.
Poslední hříčku můžeme formulovat jako „problémovou úlohu“: jak dostat energii z úplně vybité ploché baterie?
Snadno: Na hřídelku připojenou k motorku (=dynamu) namotáme nit, na její konec zavěsíme vybitou baterii – a necháme klesat. Baterie táhne nit, ta otáčí hřídelkou, dynamo dodává proud, žárovička svítí. Sice jen chvilku, ale přece.
Pokud vám tyto či podobné hříčky pomohou zpestřit výuku, splní svůj účel. A pokud snad někomu trochu přiblíží, jak se může „vyrábět elektřina“ v elektrárnách či v autě, tím lépe. Co si k nim přidáte a na co upozorníte (např. že baterie z poslední hříčky nenabude takovou rychlost, jako kdyby padala volným pádem, a proč), je už jen na vás.
Závěr
Bližší popis některých uvedených konstrukcí a experimentů bude spolu s fotografiemi součástí elektronické verze tohoto příspěvku, která bude dostupná na webu prostřednictvím serveru Fyzweb, viz [5].
Za veškeré připomínky, komentáře, náměty na vylepšení, apod. budu vděčen. A ještě malá pobídka. Zkuste zde zmiňované konstrukce a výsledky „trumfnout“. Určitě to půjde. A budeme mít zas lepší experimenty uplatnitelné ve fyzikálním vzdělávání.
Soustředění, na nichž jsme uvedené konstrukce vyvíjeli a ověřovali, byla zčásti podporována grantem FRVŠ č.B2404/2002 a rozvojovým projektem MŠMT „Učitelé fyziky v akci – nejen uvnitř školních stěn“.
Literatura
[1] Dvořák, L. et al: Pár věcí z tábora. In: Sborník z konference Veletrh nápadů učitelů fyziky 3, Praha 1998. Ed. K.Rauner, s.102-105.
[2] Dvořák, L.: Pár věcí z tábora II – tentokrát o světle. In: Sborník z konference Veletrh nápadů učitelů fyziky 4, Příbram 1999. Ed.K.Rauner. ZČU Plzeň 1999. s.35-38.
[3] Dvořák L.: Pár věcí z tábora 3 – tentokrát o čase a trochu i o elektronice. In: Sborník konference Veletrh nápadů učitelů fyziky 5, Editor K.Rauner. Praha 2000, s.147-150.
[4] Dvořák L.: Pár věcí z tábora 4 – tentokrát o zvuku. In: Sborník konference Veletrh nápadů učitelů fyziky 6, Editor O.Lepil. Olomouc 2001, s.32-38.
