Hra so silami – nitkové váhy
Ivan Baník, Rastislav Baník
Potreby: niť, spofa-páska, hmotnostný normál – závažie (môže to byť aj tabuľka čokolády známej hmotnosti), dľžkové meradlo, predmet, ktorý chceme vážiť
Príprava: O protiľahlé strany zárubne dverí prilepíme spofa-páskou konce „hlavnej“ nite (ACDB) v bodoch A a B, ležiacich na rovnakej výškovej úrovni (obr. 1). Na jednu z pomocných zvislých nití uviažeme predmet známej hmotnosti, na druhú zvislú niť uchytíme predmet, ktorého hmotnosť určujeme.
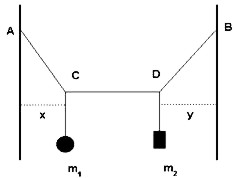
Obr. 1
Prevedenie: Pri vážení potrebujeme dosiahnuť taký stav, pri ktorom je stredný úsek CD hlavnej nite vodorovný. To sa dá dosiahnuť presúvaním závaží. Po nastavení takého stavu (po „naladení“ váh) pre neznámu hmotnosť m1 platí
![]()
kde x a y sú znázornené vzdialenosti. Tie zmeriame.
Pri domácich meraniach možno ako hmotnostný normál použiť aj tabuľku čokolády, na ktorej je hmotnosť uvedená.
Vysvetlenie: Pri analýze síl, ktoré sa pri nitkových váhach uplatňujú, si treba v prvom rade uvedomiť, že sily FC a FD (obr. 2), ktorými pôsobí vodorovná napnutá niť na uzly C, resp. D, sú navzájom rovnako veľké, ale opačne orientované (akcia-reakcia). Pre ich veľkosť platí FC = FD.
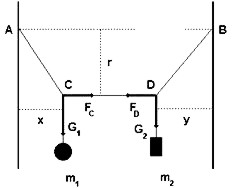
Obr. 2
V ďalšom sa zamyslime nad momentmi síl, ktoré pôsobia na úsek nite AC vzhľadom na bod A, resp. na úsek BD, vzhľadom na bod B. V prípade úseku AC ide jednak o moment sily FC, jednak o moment tiaže G1 = mg. Prvý sa – čo do veľkosti – rovná súčinu FC∙r, kde r je rameno sily FC. Druhý je daný súčinom G1∙x, kde x je rameno tiaže G1. Tieto momenty sú orientované opačne. Keďže ide o rovnovážny stav, ich veľkosti musia byť rovnaké, takže G1∙x = FC∙r.
Obr. 3
Rameno r je vlastne kolmá vzdialenosť bodu A, resp. B od priamky CD. Pri vodorovnej niti CD sú obidve uvedené vzdialenosti rovnaké.
Podobne, z podmienky rovnováhy momentov, ktoré pôsobia na úsek DB nite (vzhľadom na bod B ), plynie
G2∙y = FD∙r,
pričom rameno sily FD vzhľadom na bod B je tiež r. Z posledných dvoch vzťahov a z toho, že sily FC a FD sú rovnako veľké, vyplýva G1∙x = G2∙y,odkiaľ po rozpísaní tiaží a vykrátení dostávame
![]() .
.
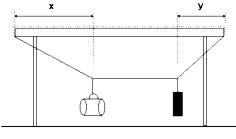
Nitkové váhy možno v domácich podmienkach vytvoriť aj na okraji stola (obr. 3). V tomto prípade má niť podobu uzavretej slučky.
Poznámky
1. Nitkové váhy s dvoma knihami
Nitkové váhy si môžeme ľahko zhotoviť aj na stole (obr. 4). K tomu použijeme dve rovnako vysoké knihy, ktoré postavíme na stôl vo zvislej polohe do tej istej zvislej roviny a do vzájomnej vzdialenosti napríklad 0,7 m. Konce nití, ktoré sú súčasťou váh, sú fixované zovretím nití vo vnútri kníh. Ako závažia pre experimenty použijeme kovové mince, patentné kľúče, kovové matice, gumy a pod.
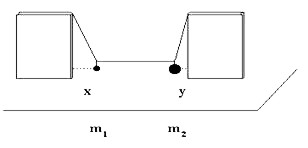
Obr. 4
Cieľom merania môže byť napríklad určiť, koľkokrát je minca 10 Sk ťažšia, ako minca 5 Sk (pre podmienky SR). Na zavesenie mince možno použiť úzky pásik spofa-pásky, kúsok etikety, alebo ľahkú drôtenú kancelársku sponku. Mince môžu slúžiť aj za hmotnostné normály.
V tejto súvislosti môže byť užitočná informácia o hmotnosti niektorých slovenských mincí (údaje o českých minciach – žiaľ – nemáme):
10 Sk |
6,60 g |
2 Sk |
4,37 g |
5 Sk |
5,41 g |
1 Sk |
3,84 g |
2. Trojramenné nitkové váhy
Istou modifikáciou opísaných nitkových váh je zariadenie znázornené na obr. 5. Ide o akési trojramenné nitkové váhy, zatiaľ čo tie klasické by sme mohli nazvať dvojramenné.
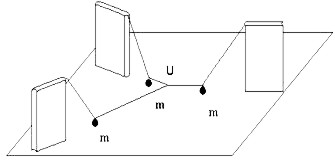
Obr. 5
V prípade nášho trojramenného nitkového „vynálezu“ nejde však o meranie hmotnosti, ale o niečo iné. Chceme ho použiť na skúmanie vektorového skladania síl. Všetky tri závažia budú mať teraz rovnaké hmotnosti m. Premiestnime ich do takých polôh, aby všetky tri nite, vychádzajúce zo spoločného uzla U, boli vodorovné. V uzle U sa skladajú tri sily, ktoré vytvárajú rovnovážnu silovú sústavu. Smer jednotlivých síl je určený smerom nití. Ak dokážeme zistiť aj veľkosť jednotlivých síl, naskytá sa možnosť overiť si graficky pravidlá skladania síl, a s tým súvisiacu rovnováhu.
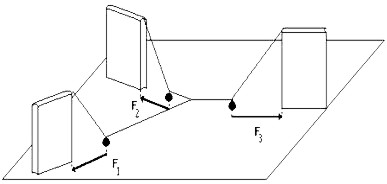
Obr. 6
Veľkosť tej ktorej sily prenášanej danou vodorovnou niťou na uzol je priamo úmerná dľžke priľahlého priemetu šikmej nite na vodorovnú podložku. Pri dôkaze si treba uvedomiť skutočnosť, že šikmý úsek nite je v rovnováhe a že teda celkový moment síl naň pôsobiacich (vzhľadom na bod závesu) je nulový.
Z uvedeného vyplýva, že pri vhodnej mierke možno pôsobiace sily prenášané jednotlivými vodorovnými niťami zobraziť aj tak, ako to ukazuje obr. 6. Každý z týchto troch „vektorov – priemetov“ sa dá posunúť do uzla. V prípade správneho postupu sa ukáže, že výslednica týchto troch vektorov je nulová.
Literatúra:
[1] Baník, R., Baník, I.: Fyzikálny experiment ako motivačný faktor II., MC Banská Bystrica, B. Bystrica 1995, 100 s.
