Exotické kmitavé sústavy

Ivan Baník

Vynútené kmity. Rezonancia

Potreby: pás galantérskej gumy (asi 1 m), závažie (jabľčko), nožnice

Príprava: Na dolný koniec gumového pásu uviažeme závažie, horný koniec pásu uviažeme o prst (obr. 1).

Ivan Baník: Exotické kmitavé sústavy - Obr. 1

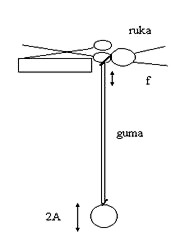
Obr. 1

Prevedenie: Experimentátor pohybuje prstom vo zvislom smere v rozmedzí, aké mu dovoľuje otvor na nožniciach. Nožnice sú jednou svojou časťou opreté o bočnú stenu skrine. Ich „oká“ však prečnievajú za okraj. Pri periodickom pohybe prsta v rámci „oka“ nožníc sa rozkmitá v tom istom rytme aj závažie, pričom amplitúda jeho vynútených kmitov výrazne závisí od frekvencie pohybov prsta. K veľkému rozkmitaniu dôjde len pri rezonančnej frekvencii.

Vysvetlenie: Ide o jednoduchý, poučný a pritom aj trochu humorný experiment, pri ktorom experimentátor pozoruje vynútené kmity závažia, zaveseného na kúsku galantérskej gumy, pod vplyvom periodickej vynucujúcej sily, vyvolanej pohybom prsta.

Poznámky:

1. S danou kmitavou sústavou sa dá ľahko „dopracovať“ aj k rezonančnej krivke. Pri pomerne rýchlom kmitaní prsta má amplitúda vynútených kmitov hodnotu, povedzme, okolo 3 mm. Pri veľmi pomalom kmitaní bude amplitúda kmitov závažia napr. 1 cm. No ak skusmo nájdeme rezonančnú frekvenciu, rozkmitáme závažie podstatne viac, napríklad tak, že amplitúda jeho vynútených kmitov bude 6 cm. Tri–štyri body poskytnú základnú informáciu o priebehu rezonančnej krivky.

2. Experiment slúži na lepšie pochopenie podstaty rezonancie.

Štipcové fyzikálne kyvadlo

Potreby: limo-trubička, ihla, dva štipce na prádlo

Príprava: Ihlu prebodneme cez limo-trubičku kolmo na trubičku (obr. 2). Potom na trubičku pripneme dva, resp. viac štipcov tak, aby ich pozdľžne osi boli rovnobežné s ihlou. Za takýchto podmienok sa štipce dajú považovať za hmotné body. Aby kyvadlo bolo schopné na ihle kmitať, treba jeho štipce pripnúť na limo-trubičku s opačnou orientáciou (v protismere), aby ťažisko sústavy nevybočilo mimo limo-trubičky. Držiakom ihly môžu byť dve knihy či dve pravítka, ktorých konce prečnievajú za okraj stola.

Prevedenie: Pre danú polohu štipcov vypočítame periódu najprv teoreticky a výsledok overíme experimentálne. Hmotnosť trubičky zanedbávame. Obdobné konfrontačné meranie vykonáme pre rôzne polohy štipcov. Jeden z nich môžeme umiestniť aj nad ihlu (os).

Ivan Baník: Exotické kmitavé sústavy - Obr. 2

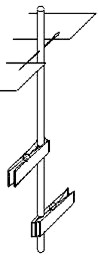
Obr. 2

Vysvetlenie: Ide o dvojbodové fyzikálne kyvadlo. Je to v istom zmysle najjednoduchšie možné fyzikálne kyvadlo (ak odhliadneme od jednobodového a teda od matematického kyvadla). Je to dvojbodové kyvadlo, tvorené dvoma hmotnými „bodmi“ a „nehmotnou“ limo-trubičkou. Hmotnosť limo-trubičky je totiž o rád menšia, ako hmotnosť bežného štipca. (Trubička má napr. hmotnosť 0,6 g, zatiaľ čo dva štipce spolu hmotnosť okolo 12 g).

Poznámky:

1. Opísané dvojbodové štipcové kyvadlo umožňuje lepšie pochopiť fyzikálne súvislosti okolo fyzikálneho kyvadla.

2. Obdobnou technikou sa dá zhotoviť aj štipcové reverzné kyvadlo, ktorého nosnou časťou je dlhá dvojitá limo-trubička. Sú to vlastne dve pozdľžne spojené trubičky. Spoj sa dá realizovať pomocou spofa-pásky. Obidve osi O₁ a O₂kyvadla sú tvorené dvoma navzájom rovnobežnými ihlami, prepichnutými cez limo-trubičku, kolmo na ňu.

Štipcové dvojniťové torzné kyvadlo

Potreby: limo-trubička, niť, dva štipce na prádlo

Príprava: Kyvadlo zhotovíme z limo-trubičky, na ktorú uchytíme dva štipce (obr. 3). Sústavu zavesíme na dve rovnobežné nite. Tie fixujeme o trubičku tak, že niť prevlečieme pomocou ihly dvakrát cez trubičku. Horné konce nití fixujeme prostredníctvom knihy.

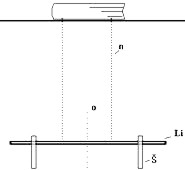
Ivan Baník: Exotické kmitavé sústavy - Obr. 3

Obr. 3

Vysvetlenie: Ak zanedbáme hmotnosť trubičky (čo je prípustné), možno naše štipcové kyvadlo považovať za dvojbodové. Máme pritom na mysli takú polohu štipcov, pri ktorej sú štipce rovnobežné s osou kmitania. Teoretický výpočet periódy takej sústavy je jednoduchý, no poučný. Direkčný moment kyvadla vzniká v dôsledku dvojice síl, ktorými na kmitajúce teleso pôsobia obe nite. Teória vedie k nasledovnému vzťahu pre periódu

kde I je moment zotrvačnosti kmitajúceho telesa, l – dľžka nití, d – vzdialenosť nití, m – hmotnosť zaveseného telesa (tentoraz dvoch štipcov).

Poznámky:

1. Opísané dvojbodové štipcové kyvadlo umožňuje lepšie pochopiť fyzikálne súvislosti okolo torzného kyvadla.

2. Lákavú možnosť pre experimentovanie poskytuje aj bežné, napr. plastové vedierko, aké sa nájde prakticky v každej domácnosti. Vedierko zavesíme na dve zvislé nite uchytené o rukoväť tak, aby rotačná os vedierka ležala v strede medzi nimi. Hmotnosť vedierka zistíme vážením. Ak zmeriame periódu T kmitov, ako aj vzdialenosť d nití a ich dľžku l, môžeme vypočítať moment zotrvačnosti I vedierka podľa hore uvedeného všeobecného vzťahu pre dvojniťové kyvadlo.

Meranie rýchlosti strely s fľašou a injekčnou striekačkou.

Potreby: Prázdna fľaša od minerálky, niť, malá injekčná striekačka.

Príprava: Fľašu od minerálky zavesíme na dve rovnobežné nite tak, že jej os je vodorovná (obr. 4). Fľaša predstavuje oscilátor, ktorý môže kmitať tak, že fľaša koná pritom len postupný pohyb. Do injekčnej striekačky natiahneme napr. 5 ml vody.

Ivan Baník: Exotické kmitavé sústavy - Obr. 4

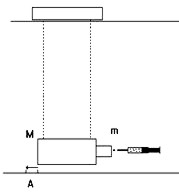
Obr. 4

Prevedenie: Vodnú strelu vystreľujeme pri pokusoch zo striekačky postavenej ústim oproti otvoru fľaše v smere osi fľaše. Vybudené kmity fľaše majú relatívne malý útlm. Kmitanie pokračuje dlhšiu dobu, ktorá postačí na pohodlné určenie amplitúdy A. Zo známej hmotnosti m fľaše, hmotnosti m_s vodnej strely a z nameranej amplitúdy A a periódy T kmitov, vieme určiť rýchlosť „vodnej strely“.

Vysvetlenie: Zo zákona zachovania hybnosti pre rýchlosť strely v_s vychádza