We live on Earth – the rotating system

Jerzy Jarosz, Aneta Szczygielska

1. Earth – the noninertial system

Five hundred years ago only the first part of this sentence was considered to be truth. Earth was considered to be at rest in the centre of the Universe. In that world should not be hurricanes, the trade winds should blow from the tropics to the equator along the meridians and a dropped stone should fall down vertically.

But everything changes. Nicolaus Copernicus, the famous monk from Poland,   appeared on the scene and ruined this order. He stopped Sun and set Earth in yearly motion around it as well as in daily motion around its own axis. Hence Earth lost its status of an inertial system.

2. Mechanical model of Earth

To prove that the rotating systems are noninertial, we can use a two-dimensional model of Earth, namely a big, flat, disc shaped vessel, which can rotate clockwise or anticlockwise with adjustable angular speed. In this system we placed the observer (a camera and Eeyore the friend of Winnie the Pooh). Another observer (Tigger, another camera and the auditory) rests in the inertial frame. In order to detect an acceleration in the rotating system, a special acceleroscope can be used to determine the direction, sense and value of the acceleration, indicated by the air bubble trapped in the water under the convex glass. When Earth is at rest there is no acceleration but when the system rotates the acceleration appears, directed towards the axis of rotation.

3. Inertia forces

So we live in a noninertial, rotating system and the inertia forces should play an essential role in our world. One of them is the well-known centrifugal force. It is directed outwards, away from the rotation axis and depends on the radius of the rotation (of course it depends also on the angular velocity). Using the model we can have
a look at how the centrifugal force acts on objects. As seen, it occurs, when the system starts spinning and it is turned outwards – the objects placed on the rotating disc, the ball and the cylinder are pushed outside. It is easy to indicate the value of the centrifugal force. It equals zero in the centre of the rotation and increases with the distance from the centre. We can notice that, when looking at special centrifugal force indicators –spheres placed on a specially shaped stands. The centrifugal force is responsible for the ellipsoidal shape of the Earth.

It is well known that the difference between the pole and equator radiuses is close to 20 km.

The less-known inertia force but, by no means, not less significant is the Coriolis force. This force acts on moving objects in such a way that it is always perpendicular to the vector of their velocity and perpendicular to the vector of the angular speed of the system as it follows from the equation:

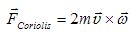
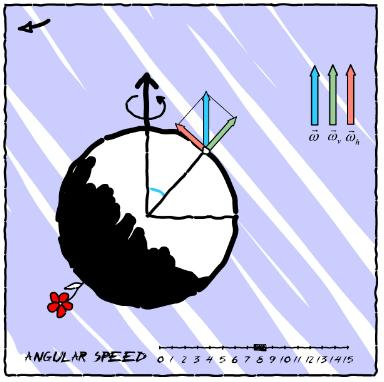
If we take into account only the vertical component of the angular velocity of the system we can say in other words that the Coriolis force deflects all moving objects to their right in the northern hemisphere and to the left in the southern one.

4. Foucault Experiment

This fact explains the complex motion of the pendulum in the famous Foucault experiment demonstrating the rotation of Earth. Looking at the pendulum in the rotating reference frame by the camera placed in the same system (the Eeyore point of view) we can observe that the pendulum traces a complicated rosette.

But observing it simultaneously from the motionless reference frame (the Tigger point of view) we can see that the pendulum retains a stable plane of swinging. It is worth noticing  that the shape of the rosette depends on the way in which the pendulum starts its motion. When we attach the pendulum with the thread to the stand, it rotates together with the system. So when we burn the thread, the pendulum will start to oscillate and the ends of the rosette will be sharp.

When the pendulum starts swinging from the motionless system, the ends of the rosette will be rounded and the pendulum will pass through the centre of the rosette.

5.  Falling stones

Using the same rotating model it can be checked that the stones on Earth do not fall down vertically. As we don’t have gravity forces directed to the centre of our model, the stones (spheres) start from the inclined support. When the Earth doesn’t rotate the stones fall down vertically, but this is no longer the case when the Earth rotates. Now the stones dropped from the tower, fall down a little bit deflected to the East when we are in the northern hemisphere and similarly (deflected also to the East) when we moved to the southern one.

The explanation is very simple. In the rotating system we have to introduce the inertia Coriolis force to explain the shape of the trajectory. The situation is different in the motionless system. The observer in the outer space – the Tigger would say that the velocity Vh of the top of the tower is bigger than the velocity V0 of the base, so a falling stone has a horizontal component of the velocity and overtakes the tower.

6. Horizontal motion

To examine how the Coriolis force works when the motion takes place in a horizontal plane and to make it easy to observe, we can use a flux of water gushing out of the hose nozzle. When we start our experiment in the northern hemisphere we can see that when the object is moving towards the pole, it is deflected to its right. If we change the direction of motion and the flux is moving towards the equator it is deflected to its right again. The same situation occurs when the direction of motion is parallel to latitude. It is worth noticing that when the object is moving along the latitude and towards the West (or East) the centrifugal and the Coriolis forces act with opposite (or the same) senses. Changing the direction of rotation and checking how it works on the southern hemisphere we easily discover that this time, the motion pointed at any direction is always deflected to its left.

So the conclusion is that the Coriolis force deflects the moving objects to their right in the northern hemisphere and to its left in the southern one regardless of the direction of the motion.

Now it is clear why the trade-winds do not blow towards the equator along the meridians. If we install in our model of Earth the equator (an outer ring) and the tropic of Cancer or Capricornus (the inner ring supported water towards the equator) we can see that the trade winds (according to the laws of physics) are deflected adequately to theirs right or left. The trade winds in turn are the driving force of the sea currents parallel to the equator and as result a counterclokwise circulation of sea currents in the north and opposite in the south.

7. Cyclones

The last phenomena, which is possible to demonstrate using rotating model of Earth are the cyclones and the whirlpools which rotate always counterclockwise in the northern hemisphere and clockwise in the southern one.

In the schematic picture we can see the way in which the deflection of motion determines the direction of rotation of hurricanes and whirlpools. Using the model and observing water sucked in by an orifice at the bottom of the rotating vessel it is well visible (colouring the water is necessary) that the whirlpools which are forming in that region are rotating always anticlockwise while the cyclones and whirlpools in southern hemisphere always rotate clockwise.

8. Conclusions

In conclusion we found that the simple rotating model can be very useful when introducing the concept of inertia forces, dependence of the description of motion on the reference frame and when explaining many important phenomena of nature on the Earth.

Note: The free CD with movies and interactive animations is possible on request. Contact: jjarosz@us.edu.pl