Laboratorní práce jako problémová úloha
Irena Koudelková
V příspěvku jsou prezentovány vybrané náměty na laboratorní práce z fyziky na druhém stupni ZŠ. Tyto práce mají formu problémových úloh a nutí žáky aktivně přemýšlet nad postupem a řešením. Náměty mohou být inspirací pro další učitele, kteří hledají cesty k zajímavé a podnětné výuce fyziky.
Úvod
Laboratorní práce z fyziky bývaly běžnou součástí výuky fyziky jak na základních, tak na středních školách. V současné době již nejsou povinnou součástí učebních osnov a učitelé je často z různých důvodů do své výuky nezařazují. Mezi důvody, proč laboratorní práce žáci nedělají, patří obvykle nedostatek času, špatné vybavení pomůckami, příliš mnoho žáků ve třídě, atd.
Ve svém příspěvku bych Vás ráda seznámila s tím, jak využívám laboratorní práce ve své výuce. Na základní škole, kde učím, máme v ročníku vždy jednu třídu s rozšířenou výukou matematiky a přírodovědných předmětů. V těchto třídách mají žáci v šestém a sedmém ročníku dvě hodiny fyziky týdně, v osmém a devátém ročníku jednu hodinu fyziky týdně a jednou za 14 dnů dvouhodinové laboratorní práce, na které se třída půlí (druhá polovina má v té době laboratorní práce z chemie). V šestém a sedmém ročníku je možné zařazovat úlohy, které mají charakter laboratorních prací, přímo do běžných hodin (viz např. zkoumání kývání kyvadla v [1]), nebo je zadávat jako dobrovolné domácí úkoly (viz [2]). Vzhledem k tomu, že při výuce podle projektu Heuréka vedu žáky k samostatnému řešení problémů, k rozvoji jejich myšlení, snažila jsem se pro výuku v osmém a devátém ročníku najít či vytvořit takové laboratorní úlohy, které budou také rozvíjet tvořivost žáků. Některé z těch úloh, které podle mého názoru tento požadavek splňují, bych vám ráda představila v tomto příspěvku.
Obecné metodické poznámky
Dříve, než popíšu, jaké konkrétní úlohy žáci řeší a zpracovávají, bych se ráda zmínila o několika obecných zásadách.
Žáci obvykle pracují ve dvojicích, pokud chce někdo pracovat sám, nebráním mu. Na první hodině laboratorních prací seznámím žáky kromě pravidel bezpečného chování při laboratorních pracích také se způsobem vypracování záznamu z laboratorní práce. Ten může mít charakter jednak „klasického“ protokolu (nadpis, úkol, pomůcky, postup, výsledky měření, závěr), ale může také obsahovat třeba popis provedených experimentů a pozorování, které žáci provedli, apod. Vždy závisí na tom, jakou úlohu či problém žáci řeší.
S žáky mluvím také o „etice experimentů“. Říkám jim, že budu mnohem raději, pokud do závěru úlohy napíšou, že jim měření nevyšlo a nenašli chybu, než když budou upravovat hodnoty tak, jak si myslí, že by měly vyjít. (Domnívám se, že s tímto způsobem zpracování úloh máme mnozí zkušenost z dob svých studií a zpracovávání protokolů z fyzikálních praktik).
Zadání úlohy, pomůcky
I v případě, kdy se jedná o standardní laboratorní práci (například určení hustoty daného tělesa), zadávám žákům pouze úkol, nikoli podrobný návod. Žáci si musí rozmyslet, jak daný úkol splní, jaké pomůcky budou potřebovat. Je-li to možné, nechávám žáky, aby si ze skříní v kabinetě potřebné pomůcky vzali sami. (Například je zajímavé sledovat, jaký odměrný válec si vezmou k výše uvedenému úkolu určení hustoty. Diskuze o tom, jestli je vhodnější válec úzký, do kterého se dané těleso sotva vejde, nebo široký, je potom důležitou součástí hodnocení práce žáků – viz dále.)
Řešení úlohy
Při hodině samozřejmě stále sleduji práci žáků. Je-li jasné, že vědí, jak budou úkol plnit, co budou dělat, nechávám je v klidu pracovat. V případě, že některá skupina dlouho váhá, neví, jak problém řešit, snažím se žáky navést ke správnému řešení, avšak nesdělit jim ho přímo. Pokud mám třídu od šestého ročníku, dětí nemívají problém přiznat, že nevědí, co s tím. Pokud ale s výukou podle projektu Heuréka v dané třídě začínám (v předchozích ročnících je měl jiný učitel), bývá to náročnější. Zpočátku mají žáci strach přiznat, že tápou, obávají se pokárání, potrestání za neznalost. Teprve postupně se učí, že se mohou i opakovaně zeptat, když něčemu nerozumí a že se na ně kvůli tomu nezlobím. Někdy se stává, že různé skupiny volí různý postup řešení. Vede-li jejich cesta k cíli, samozřejmě to nevadí.
Výsledky úlohy, hodnocení
Je-li to alespoň trochu možné, snažím se zadávat takové úlohy, ve kterých si žáci mohou sami ověřit správnost svého řešení – ať už pomocí měření jinou metodou, vhodným experimentem nebo ověřením výsledku pomocí tabulek, apod. Jsem totiž přesvědčena, že kritériem pravdy ve fyzice by v maximální možné míře měla být realita, nikoliv autorita učitele.
Abych uvedla konkrétní příklad – při měření hustoty, o kterém jsem se zmiňovala výše, používám jako tělesa o neznámé hustotě kovové válečky ze soupravy pro mechaniku. Válečky jsou označeny chemickou značkou prvku, ze kterého jsou vyrobeny, avšak na začátku osmé třídy žáci chemické značky ještě neznají a nevšimnou si jich (značky jsou málo nápadné). Po skončení práce, když některá skupina žáků dospěje k výsledku, řeknu jim, aby v tabulkách zkusili najít, o jaký kov se v daném konkrétním případě jedná (skupiny mají různá tělesa, nemohou tedy konzultovat výsledky se spolužáky). Pokud hustota tělesa zhruba odpovídá tabulkové hodnotě daného kovu (žáky na chemickou značku na tělese upozorním), diskutujeme o tom, kde asi vznikla největší chyba při měření, jak by se dala přesnost zlepšit (chyby měření ale na základní škole se žáky neurčuji). Vyšel-li žákům výsledek zcela odlišně, nechávám je najít chybu. Obvykle je největší problém v tom, že sice těleso váží s přesností na miligramy, ale při měření objemu mají přesnost pouze například 5 ml (z celkových asi 16 ml), vezmou-li si nevhodný odměrný válec. Jedná-li se o tuto chybu, obvykle ji žáci sami neobjeví, musím je k ní navést (a o problému pak diskutuji s celou třídou). Žáci pak mají možnost měření zopakovat a výsledek zpřesnit.
Tuto diskuzi považuji za nedílnou součást hodnocení práce žáků. Známka, kterou žáci dostanou poté, kdy mi přinesou zpracovaný záznam či protokol z laboratorních prací, je už jen formálním potvrzením splněného úkolu. A musím přiznat, že pro mne, ale i pro žáky, tou nejméně podstatnou částí laboratorní práce.
Příklady zadání laboratorních prací
Uvádím zde stejná zadání, jako dostávají žáci (název laboratorní práce a úkol), abyste získali představu o tom, jaké problémy žáci řeší. Úlohy komentuji, ale neuvádím podrobná řešení, předpokládám, že si je každý učitel udělá sám.
1. Úlohy, při kterých žáci něco měří
• Užití Archimédova zákona I
Pomocí Archimédova zákona urči objem daného tělesa (kamene). Pokus proveď nejdříve s vodou, potom s lihem (hustotu lihu najdeš v tabulkách). Správnost výsledku ověř pomocí odměrného válce.
Archimédův zákon patří podle mých zkušeností k nejobtížnější látce na ZŠ vůbec. Dostanou-li žáci toto zadání (bez jakéhokoliv dalšího komentáře, zhruba rok po probrání příslušné látky), musí si nejdříve vzpomenout, co vlastně Archimédův zákon říká a jak ho mohou využít při určení objemu daného kamene (při řešení úlohy samozřejmě odměrný válec k dispozici nemají). Velmi náročná je druhá část úkolu, při které si musí uvědomit, jaký vliv při měření má jiná hustota kapaliny. Správnost výsledku si žáci ověří jednak tím, že jim v obou případech vyjde přibližně stejná hodnota, jednak pomocí odměrného válce.
• Užití Archimédova zákona II
Pro danou „lodičku“ a daný „bazének“ vypočítej:
a) ponor lodičky (v cm)
b) o kolik cm stoupne voda v bazénku po ponoření lodičky
c) jaké musí být minimální množství vody v bazénku (v cm), aby lodička plavala.
Správnost výpočtu ověř experimentem.
Toto je asi nejobtížnější úloha, se kterou mívají potíže i učitelé na seminářích Heuréky. Laboratorní práce navazuje na předcházející úlohu.
Každá skupina dostane dvě kádinky různého průměru (skupiny mají odlišné kádinky). Kádinky jsou voleny tak, aby se menší z nich, ve které je trochu vody („lodička“), vešla do větší kádinky („bazénku“). Voda v lodičce funguje pouze jako zátěž, žáci ji nesmějí vylévat. Prostě kádinka s vodou představuje lodičku. Do bazénku nesmějí žáci v průběhu řešení nalít vodu (aby museli k výsledku skutečně dojít výpočtem). Žáci mají k dispozici digitální váhy, posuvné měřidlo a pravítko. Dospěje-li některá skupina k některému z požadovaných výsledků, přijdou žáci ke mně, řeknou mi očekávanou hodnotu, já naliji vodu do jejich bazénku, ponořím lodičku a změřím, zda výsledek odpovídá skutečnosti. Pokud ano, mohou pokračovat dál, pokud ne (toleranci nechávám zhruba půl centimetru), hledají, v čem udělali chybu.
Podle mých zkušeností zhruba třetina žáků ve třídě vyřeší úlohu samostatně, další zhruba třetina potřebuje lehkou pomoc, nasměrování. Každý rok se ale vyskytnou žáci, kteří si s úlohou vůbec nevědí rady, a musím jim řešení úlohy prakticky celé vysvětlit. I přesto ji ale považuji za velmi užitečnou pro rozvoj fyzikálního myšlení a představivosti.
Na závěr hodiny potom společně uvažujeme o tom, jak spolu souvisí číselné hodnoty, které v jednotlivých dílčích úkolech žáci získali. Někteří žáci již v průběhu řešení přijdou na to, že třetí výsledek mohou jednoduše získat z předchozích dvou. Pokud se to stane, pochválím je, ale požádám je, aby zkusili k výsledku dojít nezávisle.
Budete-li chtít tuto laboratorní práci zařadit do své výuky na základní či střední škole (domnívám se, že ji klidně můžete zadat maturantům, budou mít co dělat), rozmyslete si nejdříve sami podrobné řešení a ověřte svůj výsledek měřením, abyste byli schopni svým žákům či studentům poradit.
2. Úlohy, při kterých žáci provádějí experimenty, něco zkoumají, objevují
• Lom světla
Prozkoumej chování paprsku na rozhraní vzduch-voda a voda-vzduch. K dispozici máš kyvetu s vodou, úhloměr, laser (nezapomeň na dodržování pravidel bezpečnosti při práci s laserem!). Své pozorování zapiš, narýsuj chod alespoň tří různých paprsků při průchodu kyvetou, pokus se udělat závěry o velikosti úhlu dopadu a úhlu, pod jakým paprsek pokračuje vodou.
Tato laboratorní práce slouží k tomu, aby žáci objevili zákonitosti lomu světla. Zařazuji ji v době, kdy již znají zobrazení zrcadly i čočkami, lom jsme ale ještě neprobírali. První setkání s lomem paprsku na rozhraní dvou prostředí bývá pro žáky překvapivé. Na práci jim většinou stačí zhruba půl hodiny. Jsou schopni samostatně udělat závěr, že při průchodu světla ze vzduchu do vody je úhel lomu menší, než úhel dopadu, při průchodu světla z vody do vzduchu je tomu opačně. Zjistí také, že úhel lomu na prvním rozhraní je stejný jako úhel dopadu na druhém rozhraní. Je důležité žáky upozornit na to, že první poznatek platí obecně, druhý souvisí s tím, že kyveta má rovnoběžné stěny a obecně neplatí. Ve zbývající části dvouhodiny dokončíme společně látku, týkající se lomu světla. V závěru hodiny si žáci ještě vyzkoušejí svítit laserem zespoda na hladinu vody v kyvetě tak, aby pozorovali totální odraz. Tato laboratorní práce je zařazena jako součást běžného výkladu, žáci zaznamenávají svá pozorování a závěry, nepíší žádný protokol.
Mám zkušenost, že po důrazném poučení není problém s tím, že žáci používají laser s výkonem do 1 mW při skupinové práci. Pokud by některý žák nedodržoval stanovená pravidla bezpečnosti, laser bych mu sebrala a musel by pracovat pouze s baterkou (chod paprsku je pak bez zatemnění mnohem hůř vidět), nebo využít slunečního světla. Laboratorní práci, při které žáci používají lasery, lze zařadit vždy jen po zvážení, jaká je konkrétní třída, zda nehrozí úraz očí.
• Radioaktivní rozpad
Modeluj radioaktivní rozpad pomocí čočky, výsledky zapiš do tabulky, narýsuj graf závislosti počtu „rozpadlých jader“ na počtu hodů.
Pozoruj a popiš radioaktivní rozpad 137mBa, narýsuj graf závislosti počtu rozpadů za 100s na čase. Z grafu odhadni poločas rozpadu barya a porovnej s tabulkovou hodnotou.
Popiš shodné a rozdílné charakteristiky obou experimentů.
Laboratorní práce je zařazena k učivu o radioaktivitě jako rozšíření a konkretizace poznatků z výuky. První část úkolu jsem převzala z brožurky ČEZ Domácí pokusy z jaderné fyziky. Brožurka byla v poslední době inovována a doplněna dr. Zdeňkou Broklovou (viz [3]) a je k dispozici zdarma v nabídce ČEZ. Princip experimentu je ten, že každá skupina žáků má nejméně 200 zrníček čočky, z jedné strany obarvených. Zrníčka v kalíšku zamíchá a vysype na podložku. Zrnka, která jsou otočena obarvenou stranou nahoru, představují rozpadlá jádra, žáci je odstraní, spočítají a jejich počet zapíší do tabulky. Hod několikrát opakují. Grafem znázorní počet zbývajících zrnek čočky po každém hodu.
V druhé části hodiny pak společně provádíme experiment s doplňkem k soupravě Gamabeta, při kterém pozorujeme skutečný radioaktivní rozpad. Žáci zaznamenávají do tabulky počet impulzů registrovaných čítačem soupravy Gamabeta, který odpovídá počtu rozpadlých jader barya, vždy za 100 sekund (na úroveň pozadí se dostaneme zhruba po pěti či šesti měřeních, takže úloha není příliš časově náročná). Potom žáci dle zadání narýsují graf, který znázorní rozpadovou křivku a má stejný tvar jako graf, který vytvořili z experimentu s čočkou. Nakonec pak žáci formulují závěry, ve kterých popíší shodné a rozdílné charakteristiky obou experimentů a odhadují poločas rozpadu barya. Určit z reálně naměřené křivky poločas rozpadu radioaktivního prvku je pro žáky 9. třídy poměrně náročný problém. Musí si uvědomit, co vlastně toto číslo vyjadřuje a jak ho tedy z grafu získat.
• Elektrické obvody
Nakresli schémata daných elektrických obvodů, ke každému vyplň tabulku
svítí - nesvítí.
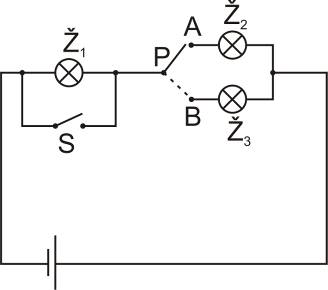
Laboratorní práci zařazuji k učivu o elektrických obvodech. Žáci v tomto tematickém celku nejdříve sestavují elektrické obvody podle daného schématu a analyzují jeho funkci (podle schématu). V této laboratorní práci řeší opačný problém – analyzovat funkci reálného obvodu se žárovkami a spínači a nakreslit jeho schéma.
Předem upozorňuji, že úloha je náročná na přípravu pro učitele. Musí navrhnout vhodné elektrické obvody a předem je sestavit (a vyzkoušet, že vše funguje, jak má). Dle mých zkušeností je pro žáky tento typ úloh dost obtížný (je jasné, že obtížnost určuje učitel tím, jak složité elektrické obvody připraví), domnívám se však, že je třeba, aby úlohy tohoto typu zvládali. Uvádím zde jeden příklad obvodů (zadání i řešení), které dětem zadávám, ale každý učitel musí samozřejmě do laboratorní práce připravit podobné úlohy, s kterými se jeho žáci již dříve setkali (neznají-li žáci zkrat, nemohu jim do laboratorní práce dát spínač paralelně k žárovce).
Já obvykle laboratorní práci realizuji tak, že v učebně připravím osm elektrických obvodů, zhruba se dvěma až třemi žárovkami a dvěma až třemi spínači či přepínači. Jednotlivé obvody jsou označené písmeny, každá žárovka a spínač jsou očíslované. Žáci pracují tentokrát sami (nikoliv ve dvojicích), procházejí po třídě a jejich úkolem je analyzovat všechny elektrické obvody, nakreslit jejich schémata a ke každému z nich vyplnit tabulku, ve které zaznamenají, které žárovky svítí při kterých polohách spínačů (název tabulky v zadání úlohy žáci znají, běžně ho používáme).
| S |
P |
Ž1 |
Ž2 |
Ž3 |
| 0 |
A |
1 |
1 |
0 |
| 0 |
B |
1 |
0 |
1 |
| 1 |
A |
0 |
1 |
0 |
| 1 |
B |
0 |
0 |
1 |

Závěr
Laboratorní práce realizované problémovou formou patří mezi nejvíc oblíbenou část fyziky v mých třídách vůbec (vyplývá to ze zpětných vazeb, které mi žáci vždy na konci roku píší). Ve svém příspěvku jsem se pokusila vám nabídnout náměty na některé z nich. Pokud byste měli zájem získat nějaké další náměty, případně si vyměnit zkušenosti s podobnou formou výuky, kontaktujte mne prosím, budu velmi ráda.
Literatura
[1] Koudelková I.: Fyzika proti matematice nebo s matematikou? Kritické listy 26, jaro 2007, s. 20-23
[2] Koudelková I.: METODIKA PROJEKTU HEURÉKA – Dobrovolné domácí úkoly z fyziky, metodický portál Mujnet http://www.mujnet.cz/PAR/clanek.aspx?a=0&prmKod=KNI.687.2577.25842636
[3] Broklová Z.: Jaderné hrátky. ČEZ Praha 2007
