Zlomky z celotáborové hry 2.republikového tábora malých debrujárů - Budislav u Litomyšle, 29.7. – 10.8.2001
Věra Bdinková

„Co událo se v pravěku
to víme, to známe
a kdo dal kompas člověku
to víme, to známe
jak slavní lidé mění svět
to víme, to známe
stroj času podá odpověď
to víme, to známe.
Refrén:
Není doba jako doba, vše se rychle mění
To co bylo včera nové, pozítří už není.
Od pazourku k internetu, tam a zase zpátky
My se času nebojíme, na nás je čas krátký“
(úryvek z celotáborové písně „Stroj času“ od Jiřího Pachla)
Celotáborová hra „Technický institut profesora Scientifixe, aneb expedice proti času“ zavedla děti – studenty prázdninového kurzu přemisťováním pomocí stroje času do dob minulých, aby se zúčastnily a aktivně zapojily do objevování technických vynálezů, či vědeckých zákonitostí. Měly možnost se také setkat s významnými vědci, učenci a techniky.
Ukázka 1
Rok 1832. Stroboskop (pohybující se obrázky)
Nezávisle na sobě vynalezli Joseph Ferdinand Plateau a Simon Stampher stroboskopický kotouč s rozloženými fázemi pohybu. Pravidelně uspořádanými štěrbinami na rotujícím kotouči nebo válci bylo možné pozorovat řadu obrázků, přičemž vznikl dojem souvislého plynulého pohybu. Byly to prvopočátky kinematografie.
Realizace
1. Každé dítě si vyrobí dle vzoru malý stroboskop (menší děti případně jiný druh pohybujících se obrázků).
2. Po oddílech si děti vyzkouší velký kotoučový a válcový stroboskop, vysvětlí si princip a mohou si podle daného pravidla do šablony nakreslit vlastní obrázkový kotouč - sestavení kotoučové filmotéky - vyhodnocení nejlepšího nápadu.
Praktické nápady:
Netopýr ( obr. 1 - pohyblivý obrázek se špejlí)
Obrázek překreslíme, přehneme, slepíme k sobě a doprostřed vlepíme špejli. Necháme dobře zaschnout. Pak otáčíme vhodnou rychlostí mezi dlaněmi. Zdá se nám, že netopýr mává křídly.

Obr. 1
Baron Prášil (obr. 2 - pohyblivý obrázek s provázkem)
Obrázek překreslíme, přehneme, slepíme k sobě. Do dírek na kraji navlečeme provázek.Otáčením provázku mezi prsty vhodnou rychlostí vidíme celého koně s jezdcem.

Obr. 2
Pumpař (obr. 3 - pohyblivý obrázek s tužkou)
Pruh bílého papíru přehneme v polovině, na horní stranu nakreslíme jeden obrázek, na spodní stranu druhý obrázek. Horní papír natočíme na tužku, kterou pohybujeme sem tam (obr 3a).
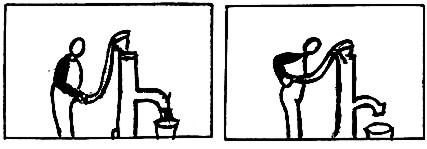
Obr. 3
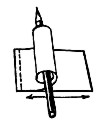
Obr. 3a
Motýl (obr. 4 -stoboskopický kotouč)
Šablonu překreslíme na tvrdý papír a vystřihneme. Na špendlík s barevnou hlavičkou navlečeme malý korálek, pak propíchneme ve středu kotouče, navlékneme větší korálek a zapíchneme do korkové zátky. Kotouč otočíme obrázkem proti zrcadlu, otáčíme jím a díváme se do zrcadla přes štěrbiny. Zdá se nám, že motýl létá.

Obr. 4
Fyzikální vysvětlení vyrobených hraček
Modely pracují na principu setrvačnosti oka, což znamená, že oko je schopno vidět obraz ještě zlomek sekundy poté co zmizel. Vzniká tak dojem souvislého plynulého pohybu.
Ukázka 2
Rok 1372 – Vrtulník
Vrtulníky jako hračky znají lidé už od 14. století. Listy rotoru, stejně jako na větrném mlýně, avšak položené horizontálně byly připevněny k držadlu na konci osy. Prudkým škubnutím za šňůru navinutou na ose se roztočily a hračka se vznesla.
Praktický nápad (papírový vrtulník)
a) Šablonu (obr. 5) zvětšíme 2krát a překopírujeme ji na tvrdý papír.
b) Šablonu přehneme dle čárkovaných čar a vlepíme jí do kruhového pásku 2,5 x 64 cm (obr. 6).
c) Ze spodu přilepíme kousek papírové trubičky (obr. 7).
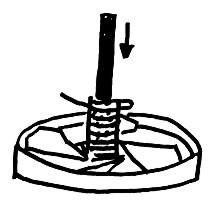
d) Na trubičku namotáme asi 60 cm provázku (obr. 8).
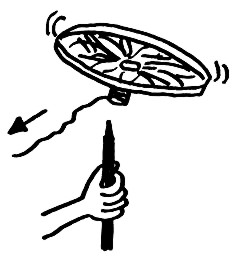
e) Trubičku nasadíme na tužku a prudce zatáhneme, za provázek, vrtulník se vznese (obr. 9).
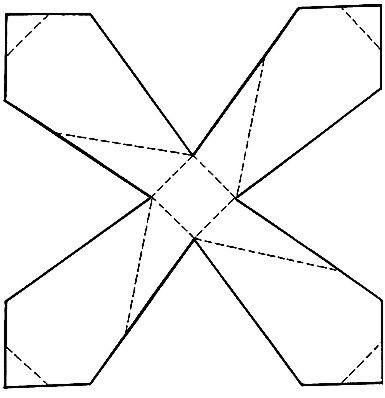
Obr. 5
Fyzikální vysvětlení hračky
Lopatky rotoru vrtulníku mají profil křídla a při rychlých otáčkách vyvolávají vztlak. Proto musíme dávat pozor na směr otáčení vrtulníku a to tak, aby byl vzduch vtlačován pod lopatky rotoru.

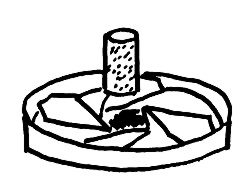
Obr. 6 (vlevo) Obr.7 (vpravo)
Obr. 8 (vlevo) Obr. 9 (vpravo)
Ukázka 3
Rok 212 př. n. l. Archimédes a jeho vynálezy
V tomto roce zemřel významný řecký učenec a vynálezce. Jeho jméno se připomíná v každé učebnici fyziky. Zjistil, že těleso ponořené do kapaliny je nadlehčováno silou, která se rovná tíze kapaliny tělesem vytlačené.Podle tohoto zákona plují po vodě těžká železná plavidla či vzduchem létají vzducholodě. Archimédes prý přišel na tento zákon, když měl vyřešit problém, zda klenotník, který zhotovil ze zlata královskou korunu, nedal do slitiny příliš mnoho stříbra. Archimédes věděl, že zlato je podstatně těžší než stříbro, stačilo mu nejprve vyvážit korunu zlatem a pak stříbrem a srovnat objem koruny s objemy stejně těžkých kusů stříbra a zlata ve vodě a mohl si tuto otázku snadno zodpovědět.
Archimédes se mezi Řeky proslavil nejvíce svými vynálezy, které se užívají dodnes. Archimédův šroub plní funkci čerpadla k zavlažování polí. Dnes je např. hlavní součástí strojku na maso, kde uvnitř válce tlačí maso na nože. Zabýval se rovněž kladkostroji a konstrukcí válečných vrhacích strojů. Je mu připisován i vynález ozubeného soukolí. Byl i matematikem. V aritmetice se zajímal o velmi vysoká čísla („0 počítání písku“), řešil mnoho geometrických úloh. Došel k metodám, jejichž pomocí mohl vypočítat obsahy a objemy různých těles. S velkou přesností stanovil poměr délky obvodu kružnice k jejímu průměru (číslo „pí“).
Mezi mnoha jinými úlohami, které řešil, byl i úkol: „Najděte poměr objemu koule vložené (vepsané) do rovnoramenného válce k objemu tohoto válce.“ Archimédes tuto úlohu vyřešil a projevil přání aby po jeho smrti bylo na jeho náhrobním kameni zobrazeno schéma této úlohy. A tak po 200 letech byl Archimédův hrob díky tomuto nákresu objeven. Archimédes nežil přímo v Řecku, ale v řecké kolonii na ostrově Sicílie ve městě Syrakusy. Ještě v 70 letech řídil obranu města proti vojskům římské říše. Římanům se podařilo lstí vniknout do města. Mezi obětmi byl i Archimédes. Legenda vypráví nejen o zapalování nepřátelských lodí pomocí zrcadel, ale i o tom, že i v době smrti byl věrný své vědě. Když se římský voják rozmáchl mečem aby ho zabil, Archimédes ho požádal: „Pozor, nesmaž mi mé kruhy.“
Praktická realizace
Tato etapa byla realizována formou bojové hry v terénu, při které se děti seznamovaly s některými vynálezy Archiméda a hledaly jeho náhrobek. Celá hra začala hranou pověstí o životě a díle Archiméda a známou písničkou Šimka a Grossmanna „Archimédův zákon“
V terénu bylo zvoleno několik stanovišť (z toho dvě u rybníka) Každý oddíl obdržel mapu s vyznačenými stanovišti a v určeném pořadí je navštěvoval.
Příklady úkolů
1. Zavěs velký kámen na prádelní šňůru a pozoruj sílu, kterou potřebuješ k uzvednutí kamene.
a) ve vzduchu
b) těsně pod hladinou vodu
c) ve větších hloubkách
2. Na tři pokusy „zapal“ plachty nepřátelské lodi (nasměruj zrcadlem sluneční paprsek na nakreslenou loď.
3. Zvolte tři zástupce a štafetovým způsobem rozeber a slož mlýnek na maso. (jak souvisí tento úkol s tématem naší hry?)
4. Po cestě najdi kámen o hmotnosti 1kg a prověř si svůj odhad pomocí páky. Máš tři závaží, dva sáčky s pískem a plastovou láhev s jedním litrem vody.
5. Na dně nádoby s vodou leží alobalová koule. Co uděláš, aby alobal plaval ? Může plavat alobalová koule ?
6. Pomocí sudu plného vody urči objem táborníka (kromě hlavy)
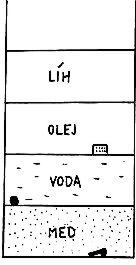
7. (obr. 10)
a) Urči, která kapalina má největší hustotu.
b) Které ze tří tělísek má nejmenší hustotu.
8. Vyber správnou odpověď: červené plastové těleso má hustotu:
větší než líh a větší než voda
menší než voda a menší než líh
větší než líh a menší než voda
stejnou jako všechny čtyři kapaliny
9. Čtverec má 9 polí. Na první pole položíme jedno zrnko, na druhé pole dvojnásobek, na třetí pole dvojnásobek počtu zrn na druhém poli…, kolik zrn je na devátém poli.
10. Z daných částí slož mapu, která tě dovede k náhrobku Archiméda. Zjisti, jaký nápis je na něm vytesán.
Obr. 10
