Tri triky z optiky
Ivan Baník, Rastislav Baník
V príspevku opíšeme niekoľko netradičných experimentov vhodných pre účely školskej fyziky. Hodia sa aj pre individuálne experimentovanie žiakov v bežných domácich podmienkach.
1. Index lomu vody (metóda jednej priamky)
Čitateľovi je iste dobre známy fakt, že zdanlivá hľbka mince nachádzajúcej sa na dne jazierka je menšia, ako hľbka reálna. Pomer reálnej a zdanlivej hľbky (pri pohľade zhora) je pritom rovný relatívnemu indexu lomu vody (vzhľadom na vzduch). To v zásade umožňuje určiť index lomu vody. Pri realizácii takého merania s pohárom vody nám pomôže trik.
TRIK 1
Sklený pohár s priehľadným, rovným tenkým dnom naplníme vodou a postavíme na kus papiera, na ktorý sme predtým nakreslili rovnú čiaru c (obr. 1). Tú pozorujeme cez vodu okom umiestneným nad pohárom. Obraz c′ čiary sa vytvára v menšej hľbke, ako je hľbka a predmetu pod pohárom.
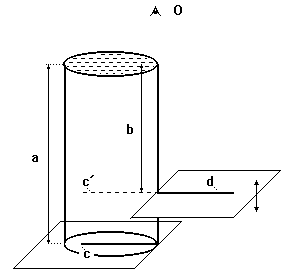
Obr. 1
Na určenie obrazovej vzdialenosti b použijeme iný papier s čiarou d. Ten umiestníme tesne vedľa pohára tak, aby obe čiary (zdanlivá v pohári a reálna vedľa neho) ležali v jednej priamke. Aby sme to dosiahli, musíme vonkajší papier umiestniť vo vhodnej výške nad úrovňou stola. Priamkovitosť oboch úsekov (čiar) overujeme pozorovaním čiar z rôzných uhlov pohľadu pri vodorovnom premiestňovaní oka v smere kolmom na čiary.
Po dosiahnutí „priamkovitosti“ zmeriame predmetovú a obrazovú vzdialenosť. Predmetová vzdialenosť a je určená vzdialenosťou papiera pod pohárom od hladiny vody. Obrazovú vzdialenosť b udáva vzdialenosť vonkajšieho papiera od hladiny vody. Pre index lomu vody platí n = a/b. Vychádza hodnota blízka hodnote 1,33.
2. Totálny odraz (zrkadlo z krabičky tik-taku a z drevenej doštičky)
Krabičku tik-taku možno premeniť na dokonalé zrkadlo. Umožňuje to trik 2.
TRIK 2
K pokusu potrebujeme v prvom rade priehľadnú krabičku K tik-taku, z ktorej odstránime obvyklú nálepku na jej hornej časti, resp. aj oddeliteľný vrchnáčik s dvierkami. Pomocou gumičky do vlasov krabičku pripevníme o koniec priehľadného celuloidového pravítka P tak, ako ukazuje obr. 2a. Otvor krabičky je pritom v dolnej polohe.
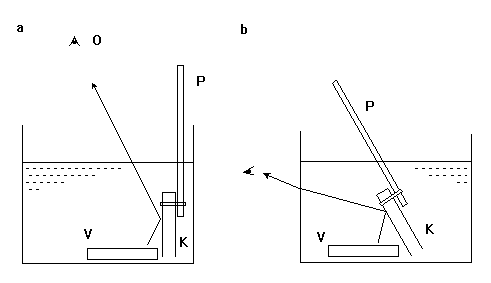
Obr. 2
Najlepší efekt pri pozorovaní dosiahneme tak, že na dno priehľadnej nádoby s vodou umiestníme pestrofarebný plechový vrchnáčík V z nejakého zaváracieho pohára. Pomocou pravítka, ktorého horný koniec držíme v ruke, krabičku ponoríme do vody. V krabičke zostáva pritom vzduch. Práve jeho prítomnosť umožňuje pozorovať totálny odraz na príslušnom rozhraní. Pri pohľade zhora - tak ako ukazuje obr. 2a - sa nám zvislá stena krabičky javí ako dokonalé zrkadlo, v ktorom vidíme pestrofarebný obraz vrchnáčika. Zrkadlenie je celkom podobné ako v prípade bežného vreckového zrkadielka, ktoré - pre porovnanie - upevníme obdobným spôsobom na iné pravítko.
Totálny odraz, ktorý je zodpovedný za perfektné zobrazenie, vzniká vďaka tomu, že aktuálne lúče dopadajú na príslušné rozhranie pod väčším uhlom, ako je medzný uhol.
Pri pohľade cez bočnú stenu nádoby s vodou (držiac pravítko vo zvislej polohe) sa nám však krabička javí ako priehľadná. To preto, že v tomto prípade nie sú splnené podmienky pre totálny odraz.
Demonštračná verzia experimentu
Pre demonštračné účely je vhodnejšia trochu odlišná verzia experimentu. Znázorňuje ju obr. 2b. Pri nej je pravítko P s krabičkou K naklonené a žiaci pozorujú obraz pestrosfarbeného vrchnáčika v „tika-takovom“ zrkadle cez zvislú bočnú rovinnú stenu priehľadnej nádoby s vodou. Povrch krabičky dokonale zrkadlí len pri postačujúcom naklonení pravítka. Ak je pravítko vo zvislejšej polohe, zrkadlenie nenastane a krabička sa nám javí ako priehľadná. Pri zmenách sklonu pozorujeme zmeny odrazivosti.
Pochopiteľne, že namiesto krabičky tik-taku môžeme použiť aj nejakú inú priehľadnú krabičku vhodnej geometrie. Podmienkou je však, aby pri jej ponorení zostal v nej vzduch.
Pokus s valcovým pohárom
Efekty súvisiace s totálnym odrazom sa dajú pozorovať aj pri ponorení valcového skleného pohára do vody tak, že v pohári je vzduch. Otvor pohára je pritom buď dole, alebo hore nad hladinou vody. Zakrivená bočná valcová stena pohára sa nám pri pohľade zhora javí ako valcové zrkadlo, v ktorom vidíme zobrazený farebný vrchnáčik umiestnený na dne. Pokus je však menej efektný, ako pri „rovinnom zobrazení“.
Aj drevenú doštičku možno premeniť na zrkadlo. Umožní nám to trik 3.
TRIK 3
Ak chceme z drevenej doštičky d vytvoriť dokonalé zrkadlo, musíme ju najprv vložiť do lesklého priehľadného obalu na spisy tak, aby pri ponorení doštičky s časťou obalu neprenikla k doštičke voda (obr. 3). Ak je doštička vo zvislej polohe, môžeme totálny odraz na nej pozorovať pri pohľade zhora. Povrch doštičky sa javí ako dokonale zrkadliaci. V takom „zrkadle“ jasne vidíme farebný obraz ponoreného farebného vrchnáčika, práve tak, ako tomu bolo v prípade pokusu s krabičkou tik-taku.
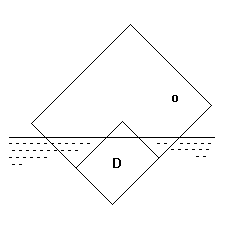
Obr. 3
Ak však sústavu dostatočne nakloníme, obraz vrchnáčika môžu pozorovať žiaci aj cez zvislú rovinnú bočnú stenu nádoby s vodou. Ak však doštičku postupne vstyčujeme do zvislej polohy, totálne zobrazenie vrchnáčika v našom „drevenom zrkadle“ sa stráca a doštička v obale sa nám bude javiť ako drevená.
Treba zdôrazniť, že za pozorovaný jav nenesie zodpovednosť samotná drevená doštička, ale v podstate vzduchová vrstvička medzi doštičkou a priehľadným plastovým obalom, do ktorého je vložená. Totálny odraz nastáva na rozhraní obalu a vzduchu tenkej vzduchovej vrstvy. Doštička plní vlastne len geometrickú funkciu a to tým, že zabezpečuje rovinnosť sústavy. Do plastového obalu môžeme vložiť ľubovoľnú rovinnú platňu s podmienkou, že vo vnútornej medzere sa vytvorí tenká vzduchová vrstva.
PRÍLOHA Exotická šošovka - rozptylka vo vedierku
Vodnú rozptylku vytvoríme z vody, nachádzajúcej sa v menšom otáčajúcom sa priehľadnom vedierku. Roztočenie vedierka s vodou dosiahneme pomocou tenšieho špagátu, na ktorý vedierko zavesíme. Horný koniec špagátu dobre natočíme medzi prstami ešte pred zdvihnutím vedierka. Počas začínajúcej rotácie špagát prstami natáčame ešte aj ďalej. Tak dosiahneme postačujúce obrátky sústavy a dôsledkom toho aj vznik duto (parabolicko)-ploskej vodnej šošovky. V jej centrálnej oblasti ju možno považovať za guľovo-ploskú.
Vzniklá vodná rozptylka ma zobrazovacie schopnosti, ktoré môžeme sledovať aj tak, že pod rotujúcu vodnú šošovku umiestníme farebný vrchnáčik zo zaváracieho pohára a ten sledujeme zhora cez šošovku. Obraz vrchnáčika sa nám bude javiť výrazne zmenšený, čo sa v priebehu spomaľovania rotácie postupne mení.
Poznamenajme, že experiment s vedierkom a vodou poslúži aj v hydromechanike na demonštráciu vlastností rotujúcej kvapaliny a na pozorovanie parabolického profilu hladiny.
Literatúra
[1] Baník I. - Baník R.: Niekoľko zaujímavostí z optiky. Zborník „Šoltésove dni - 6“, Bratislava, 14. - 16. decembra 2000 (v tlači).
