About paper
Czech originalExperiments on the Basics of Electrostatics (Coulomb’s law; Capacitor)
The physics textbooks open the chapter about electricity and magnetism with the topic of electrostatics and so do most teachers. This article deals with two basic concepts of this topic – capacitor and the Coulomb’s law – and gives suggestions for a few experiments that could help students to understand better related physical phenomena and to get hands-on experience themselves.
Proposals for described experiments were found in [1], [2] and [4].
A Simple Capacitor
Capacitor is an electrical component which can be used for storing electric charge and also as a temporary voltage source. Capacitors can have many different shapes and constructions but the basic variant – that gave rise to its schematic symbol – is a pair of parallel conductive plates separated with air or another dielectric.
The equation for the capacitance of a planar capacitor (1) is simple to deduce. It is also simple to verify however, this probably does not happen in many cases. If a teacher does not have a demonstrational capacitor (two planparallel plates that can be set in different distances and the effective area of which can be changed), he can substitute it with two pieces of common aluminium foil connected to a multimeter that can measure capacitance. \[\tag{1} C = \epsilon \frac{S}{d}. \]
The whole idea is very simple. We make the plates of the capacitor from two pieces of aluminium foil that we place between different leaves of a book. The plates should be approximately as large as the pages in the book. We measure the capacitance of such capacitor with the multimeter. We change the number of pages between the plates to determine the dependence of capacitance C on the distance between the plates d. We plot the dependencies C(d) and C(1/d) in two graphs. The distance can be scaled in millimeters or in number of the pages. The latter is simpler, faster and in my opinion better because students are not distracted from the dependence of capacitance on distance by converting pages to millimeters. Students can see which of the two graphs seems to be linear and thence if capacitance C is proportional to d or 1/d (Fig. 1 and 2).
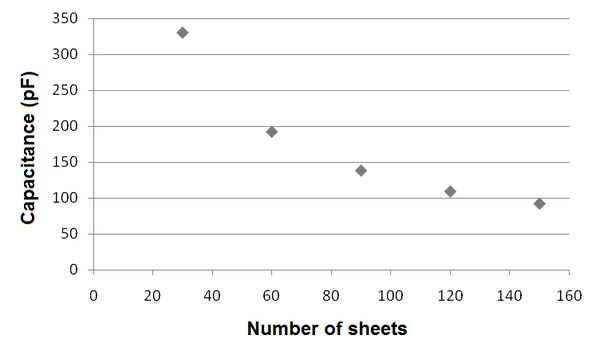
Fig. 1: Experimental dependence of capacitance on the number of sheets between the plates of the capacitor
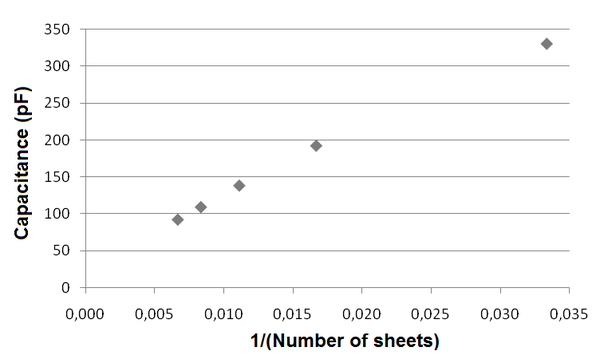
Fig. 2: Experimental dependence of capacitance on reciprocal number of sheets between the plates of the capacitor
To get the dependence of capacitance C on the effective area of the plates A, we only have to fold the plates in half[1] and measure their capacitance, fold them in half once more, measure again and so on. We write the area in multiples (fractions) of the original plate area. We let students plot the dependences C(A) and C(1/A).[2] Students will find out again if capacitance C is proportional to A or to 1/A.
Combination of the two derived dependencies gives the proper combination of A and d in equation (1).
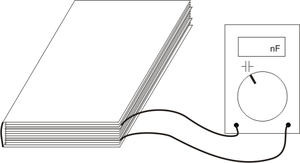

Fig. 3: Measuring the capacitance of a self-made capacitor: a) scheme b) real connection
Material
· aluminium foil
· thick book (the larger format the better)
· multimeter capable to measure capacitance
· conductors with crocodile clips, possibly a slide calliper and a ruler
Example of a Worksheet
Part I – The dependence of capacitance of two plates (foils) on the distance between them
1) Obtain a thick book and two pieces of aluminium foil in size of the book pages.
2) Place the foils in the book leaving 30 sheets between them (put one foil on page 200 and the other on the page 260 for example).
3) Connect the red probe of the multimeter to one foil and the black one to the other and close the book.
4) Turn the selector of the multimeter on the “–||–” symbol (measuring capacitance)
5) Measured capacitance is most probably in nanofarads. (You should see the sign “nF” on the display.) Write down the measured capacitance in the table below.
6) Repeat the measurement with different numbers of pages between the foils.
7) Put obtained data in Excel or another spreadsheet program and plot the following:
a) scatter plot of capacitance as a function of the number of sheets
b) scatter plot of capacitance as a function of the reciprocal number of sheets.
| Number of sheets |
(Number of sheets)-1 |
Capacitance (nF) |
| 30 |
1/30 |
|
| 60 |
1/60 |
|
| 90 |
1/90 |
|
| 120 |
1/120 |
|
| 150 |
1/150 |
|
Which of the plots looks linearly?
a) Capacitance vs Number of sheets
b) Capacitance vs (Number of sheets)-1
A linear dependence shows that the quantities are proportional to each other. Which of the following proportions is thence correct? (C denotes the capacitance of the capacitor and d the distance between the plates (foils). The distance corresponds to the number of sheets between the foils.)
\[ C \sim \frac{1}{d} \qquad C \sim d \]Part II – The dependence of capacitance of plates (foils) on their size
1) Measure and write down the capacitance of your capacitor with some 50 sheets between its plates.
2) Repeat the measurement with different area of the foils. Fold the foils in half before each new measurement. Write down measured capacities in the following table.
3) Plot two graphs with your data in Excel:
a) Scatter plot of capacitance as a function of the area of the plates,
b) Scatter plot of capacitance as a function of (the area of the plates)-1.
| Area |
(Area)-1 |
Capacitance (nF) |
| A |
1 / A |
|
| 0.5 * A |
2 / A |
|
| 0.25 * A |
4 / A |
|
| 0.125 * A |
8 / A |
|
| 0.0625 * A |
16 / A |
|
Which of the plots looks linearly?
a) Capacitance vs Area
b) Capacitance vs (Area)-1
Linear dependence means that the quantities are proportional to each other. Which of the following proportions is correct? (C is the capacitor’s capacitance, A is the area of its plates.)
\[ C \sim \frac{1}{S} \qquad C \sim S \]Part III – The equation of capacitance of a plate capacitor
Combine both obtained proportions to formulate one that contains both quantities (dependence of capacitance C on both d and A).
\[ C \sim \]To turn the proportion to a real equation (with proper units), we must add a proportion constant. In this case it is ε which is called the permittivity of the material between the plates. Vacuum has the lowest permittivity of all materials (\(\epsilon_0 = 8.85\,\mathrm{C^2/Nm^2} \)). The permittivity ε of any other material is larger and is given as a multiple of vacuum permittivity ε = εrε0, where εr is this multiple which is called the relative permittivity of the material.
Fill in the quantities in the equation of the capacitance of a plate capacitor.
\[ C = \epsilon \frac{\ }{\ } = \epsilon_r\epsilon_0 \frac{\ }{\ } \]Other Possible Application of the Set
If we measure the distance between the plates (aluminium foils) in meters, we will be able to calculate the relative permittivity of the material between the plates. The permittivity of paper is about εr = 3.5. [2]
Moreover we can show [3] with folded foils that the area A in the final equation is not the area of the plates themselves but their “effective” area which means the area at which the plates overlap.[4]
Verification of the Coulomb’s Law
Coulomb’s law (2) is one of the fundaments of electrostatics that is taught at the high school. How can we simply verify or deduce this law?
\[\tag{2} F_e = \frac{1}{4\pi\epsilon} \frac{Q_1 Q_2}{r^2} \]The Coulomb’s law. Between two point charges there acts an electrostatic force. This force is proportional to the magnitudes of the two charges and inversely proportional to the square of the distance between them. The force is repulsive between two charges of the same sign and attractive for charges of opposite signs.
Here, we will not describe verification of the whole law but only the dependence of the force Fe on the distance r and on the magnitude of the charges Q1 and Q2.
We will need: high-voltage source (or Wimshurst machine or van der Graaff generator etc.), three ping-pong balls sprayed with a conductive paint (or smaller Christmas baubles) on insulating stands (we used plastic straws), digital scales with precision at least 0.01 g, a ruler and some stands and holders (see Figure 4a).


Figure 4: a) Coulomb’s law demonstration setup b) Digital scales “measuring” the electrostatic force
The whole principle of measuring the electrostatic force is quite simple. We use the scales to measure the force acting on a ball. It is ideal if the scales have the tare function[5].
· We put one of the balls on the scales and another one in a holder vertically just above (but not too close to) the first ball.
· We set zero on the scales.
· We charge the balls. In our case (Figure 2) we touched each ball with a conductor connected to the same clip of the high-voltage source. Now both the balls have a charge of the same sign and magnitude.
· We lower the upper ball near to the lower one.
· We read the “added weight” Δm of the lower ball on the scales. The electric force Fe' acting between the balls is directly proportional to Δm as Fe& = Δm·g.
· We measure the distance between the centers of the balls r.
Because our balls are not point-like, the charge on their surfaces rearranges a little bit in presence of the other charged ball. This rearrangement changes the electrostatic force between the two balls to a more complicated shape[6]
\[\tag{3} F_e' = \frac{Q_1 Q_2}{4\pi \epsilon r^2} \cdot \left[ 1- 4\cdot \left( \frac{a}{r} \right)^3 + 14\cdot \left( \frac{a}{r} \right)^6 - \ldots \right] \]where a is the radius of the balls. The correction term \( 14\cdot\left( \frac{a}{r} \right)^6 \) is much smaller than the first one and so are all terms after this one and we can neglect them:
\[\tag{4} F_e' = \frac{Q_1 Q_2}{4\pi \epsilon r^2} \cdot \left[ 1- 4\cdot \left( \frac{a}{r} \right)^3 \right] \]Verification of Proportionality Fe ~ 1/r2
Since we want to verify the dependence of electrostatic force on the reciprocal square of the distance r we will not plot a graph of the force \( F_e' = \Delta m \cdot g \) which we measure but the force that would correspond to point charges of the same magnitude as the charge on our balls
\[\tag{5} F_e = \frac{F_e'}{\left[1-4\left(\frac{a}{r}\right)^3 \right] } = \frac{\Delta m \cdot g}{\left[1-4\left(\frac{a}{r}\right)^3 \right] } \]The reason for this modification is that Excel (as well as most of available spreadsheet applications) is capable to fit only some pre-defined functions to a set of data and the dependence in equation (4) is not one of these, but a power dependency is. After this correction we are verifying the original dependence (2) of the force Fe that would be acting between the balls if the charges did not rearrange on their surface.
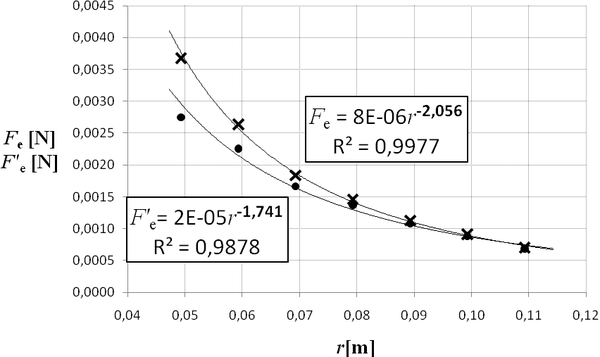
Fig. 5: Comparison of the measured force Fe' (dots \( \bullet\) ) and the corrected point-like force Fe (crosses \(\times\) ).
In Figure 5 we can see that the correction gives data that correspond well to the Coulomb’s law and that the smaller is the distance between the balls the larger is the correction.
Demonstration of the Dependence Fe(Q1, Q2)
We again set two charged balls at a fixed distance (one of the balls is placed on the scales – as it was in the previous case) and read the weight on the scales. Then we touch one of the balls with a third, uncharged ball – one half of the charge that was on the touched ball moves to the third ball. When we put the third ball away, we can see that the scales show half the weight than before.
Conclusion
You have most probably come upon many other possibilities how to use shown experiments. It is possible to compare permittivities of different kinds of material (glass, wood, plastic etc.) in the first method. In the second experiment we can charge the balls with opposite charges and see a negative value of the force on the scales etc.
This article was supported with the grant FRVŠ 1237/2010: Demonstrational experiments for the lectures "Physics I" and "Classical electrodynamics".
References
[1] Capacitor lab - using a capacitor in a circuit. online. [cit 2010-09-02] http://webapps.lsa.umich.edu/physics/demolab/controls/FileExp.aspx?fileid=36
[2] Experiment: Parallel Plate Capacitors. online. [cit 2010-09-02] http://spot.pcc.edu/~azable/ph213/labs/213Lab4-Parallel_Plate_Capacitors.doc
[3] Permitivita. online. http://cs.wikipedia.org/wiki/Permitivita. [cit. 2010-09-01]
[4] Cortel A., Demonstrations of Coulomb’s Law with an Electronic Balance, Physics Teacher, v37 n7 p447-48, Oct 1999
[5] Larson C.O., Goss E.W., A Coulomb's Law Balance Suitable for Physics Majors and Nonscience Students, American Journal of Physics, v38, n11, pp1349-1352, Nov `70
[1] Halving is not sufficient for a more precise measurement. If we wanted more accurate measurement, we would need more values.
[2] We do not show the graphs this time to spare space. We are sure you can imagine them.
[3] Some students will probably notice this themselves during the measurements.
[4] This can cause some troubles during the students‘ work. We could avoid it if we folded only one of the foils. On the other hand, problematic situations make students try to solve the trouble themselves.
[5] the option to reset zero.
[6] Article [5] deals with derivation of the correction of Coulomb’s law for definite-size balls. The need for the correction is obvious in Figure 5.