About paper
Czech originalAn Experimental Study of Sudden Crystallization of Supercooled Water
Nina balanced the piece of ice two or three times in her hand, and threw it forward with all her strength. A sudden thrill seemed to vibrate across the motionless waters to the distant horizon, and the Gallian Sea had become a solid sheet of ice!
Jules Verne, Off on a Comet
Supercooling, also known as undercooling, is a well known phenomenon at which a substance exists in the liquid phase at temperatures below its freezing point at given pressure. Undercooled water is commonly found in clouds where its temperature in the liquid phase can reach down to -40°C. Sodium acetate (respectively its trihydrate) that gives out latent heat upon initialization of crystallization in heating pads is also deeply supercooled.
This phenomenon is related to creation of crystallization nuclei that trigger the phase transition. We will explain it with certain simplification by the following energetic considerations. [1]
Let us presume that a small solid phase nucleus emerges by random fluctuation in the liquid. The creation of the nucleus is connected to creation of stronger chemical bonds that lower the energy of the system by the value ΔEV. This is the energy that is released as the so called heat of solidification (or fusion). A new solid-liquid interface that is connected to the surface energy ΔES emerges simultaneously. (Surface energy is mentioned in lectures concerning surface tension of liquids in high school physics.) For the total change of the energy of the system ΔEC we can write[1] \[\tag{1} \Delta E_C = \Delta E_V + \Delta E_S = -Ar^3 + Br^2, \]
where r is the radius or another characteristic size of the nucleus and A and B are the material constants. The negative sign describes a drop of energy (proportional to the volume of emerged nucleus here), the positive sign its increase (proportional to the surface of the interface). Figure 1 gives a graphical representation of described dependencies.
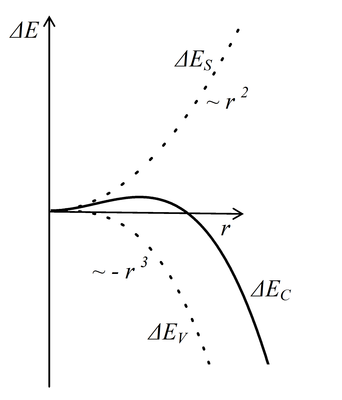
Fig. 1
Mentioned reasons show that the energy of the system increases during the initial stage of the growth of the nucleus and thence it does not take place spontaneously just as the water does not spontaneously flow up the hill. Nevertheless, a nucleus can exceed the critical size by random fluctuation when the liquid is deeply cooled and thence break the energetic barrier and finally commence the phase transition. This is called homogeneous nucleation. The so called heterogeneous nucleation takes place much more often. In this case the nucleus emerges on an impurity or a defect that lowers the surface energy of the nucleus. This leads to lowering of the critical size and facilitates the creation of a nucleus of supercritical size.[2]
The phase transition goes on very fast once any of the nuclei exceeded the critical size. However, latent heat that is released during solidification heats up the mixture. The phase transition stops and equilibrium state is reached at the moment when the freezing point is reached by the heating.
The amount of ice in the case of suddenly solidified water is quite small. We can find this simply by a simple calculation using the calorimetric equation \[\tag{2} m_1 c (t-t_p) = m l_t ,\]
where m1 is the initial mass of supercooled water, m is the mass of created ice, tp is the temperature reached by supercooling, lt is the heat of fusion of ice and t is the final temperature of the mixture (the freezing point). After substitution and calculation of appropriate values we can see that each degree of Celsius below the freezing point corresponds to 1.2 % of ice in the mixture. Thence, J. Verne was wrong when he described the freezing of the Gallian sea accompanied by a sudden thrill. Sparse brash-ice would form instead of a solid sheet of ice and no loud cracking sound can be expected during its formation.
Measuring of the amount of solidified ice presents an interesting experimental problem. There is only little ice sparsely floating in the water in standard experiments and it cannot be easily separated. The mixture of water and ice receives heat from its surroundings during manipulation at common laboratory temperature and the fine frazil usually melts quickly. Two indirect methods for measuring the amount of ice were tested.
Calorimetric method
We pour the content of the vessel – a PET bottle – into a calorimeter immediately after the end of crystallization and stir warm water into the mixture until all the ice melts. Melting is described by the following calorimetric equation \[\tag{3} m_2 c (t_2-t_p) = m l_t + m_1 ct,\]
where m2 is the mass of warm water, t2 is its temperature and t is the final temperature of the mixture (expected slightly above 0 °C). It is convenient to choose the temperature of the warm water identical to the room temperature and to chill the calorimeter with a mixture of water and ice to 0 °C in advance to limit side losses or gains of heat during the measurement. We do not have to incorporate the capacity of the calorimeter in equation (3) under these conditions. The amount of used warm water is most easily found out by weighing the vessel with it before and after the experiment.
Measurement of the volume change during crystallization
This experiment is more demanding both in preparation and in realization. The basic idea is based on the well known fact that ice is less dense than liquid water and a partial crystallization must be accompanied by an increase of the total volume of the mixture. Because only a few per cents of ice emerge and its density differs by less than 10 % from that of water, the total change of the volume of the mixture will be smaller than 1 %. It is thence clear that we have to realize a fine and sensitive experiment.
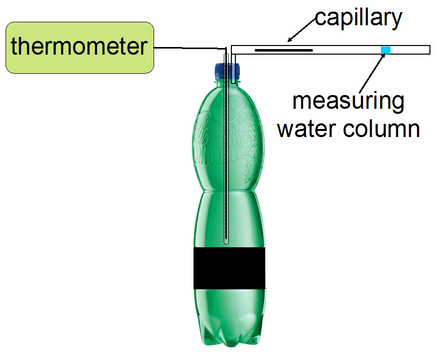
Fig. 2
We measure the change of the volume from the shift of a short water column in a glass tube that is connected to the inside of a hermetically sealed PET bottle with a rubber tube. Volume calibration of the glass tube is most easily carried out if we weigh it empty and then filled with water on sensitive scales. Because crystallization is most easily initiated by a punch, it is good to place a glass capillary between the measuring tube and the bottle to suppress a sudden change of pressure during the blow in the measuring tube and thus protect the water column from tearing. We can measure the temperature in the bottle simultaneously with a thermocouple placed in another glass tube (sealed at the bottom) that is airtightly stuck in the bottle cap. By placing the thermocouple in a glass tube we avoid a direct contact of the thermocouple with undercooled water that would increase the probability of creation of a nucleation site on the thermocouple.
The volume of undercooled water VV and of the mixture of water and ice VS are described by following equations \[\tag{4} V_V = \frac{m_1}{\rho_V}, V_S = \frac{m_1-m}{\rho_V} + \frac{m}{\rho_L} \]
where ρV is the specific weight of water and ρL that of ice. From (4) we get the equation for the unknown mass of ice m \[\tag{5} m = \frac{(V_S-V_V)\rho_L\rho_V}{\rho_V - \rho_L} .\]
It is clear that the experimental values have systematic errors. It is not possible to avoid heating up of the mixture during manipulation in room temperature conditions. This systematically lowers measured mass of ice. Warming of the air in the measuring tube will affect the measurement probably the most. We may partially correct this error in the following way:
Let us presume that the air that is pushed out from the bottle during crystallization has the same temperature as the undercooled water. This air is warmed up in the joining tube to the temperature of the surroundings. The change of its volume ΔV is given by the state equation of an isobaric process \[\tag{6} \Delta V = \frac{t_2 - t_p}{T}(V_S - V_V) ,\] where T is the arithmetical average of temperature t2 and tp in kelvins. The measured mass of ice with this correction is then \[\tag{7} m=\frac{(V_S-V_V-\Delta V)\rho_L\rho_V}{\rho_V - \rho_L} .\]
Both described methods can be used simultaneously during one crystallization and give two independently measured numbers allowing direct comparison. If we measure the temperature of undercooled water during the measurement too, we get a third independent entry calculated directly from equation (2).
The results of several experiments are shown in the following table.
| total mass of water (g) |
reached supercooled temperature |
mass of ice (g) | |||
| calculated from eq. |
calorimetrically measured |
from change of volume | |||
| without correction (5) |
with correction | ||||
| 500 |
- 5.4°C |
34.0 |
34.8 |
37.7 |
34.1 |
| 525 |
- 4.7°C |
31.1 |
21.3 |
29.6 |
26.6 |
| 525 |
- 4.6°C |
30.5 |
22.3 |
29.6 |
26.6 |
| 1500 |
- 3.8°C |
71.9 |
47.7 |
53.2 |
48.2 |
| 1500 |
- 5.0°C |
94.6 |
58.8 |
72.8 |
65.1 |
The data in the table present a representative selection from a higher number of measurements that includes both more and less successful experiments. The value calculated from equation (2) differs the most from other methods in most cases. The reason for that is that the thermometer measures the temperature only at one point in the bottle while the distribution of temperature is surely not homogeneous. We cannot achieve a more homogeneous distribution by stirring the water because that would initiate crystallization too soon. The only way for a better determination of the mean temperature of supercooled water is simultaneous measurement of its temperature at more than one spot. This would make the task much more complicated therefore we did not carry out such a measurement.
The amount of ice calculated from the change of the mixture’s volume is systematically higher than the one that was measured calorimetrically. This can be partially explained by the fact that calorimetric measurement must be carried out with some delay after determination of the change of volume. The mixture is receiving heat from the surroundings and some of the ice melts prematurely during this time.
The correction on the warming of the air acted in the right direction every time. This supports its justifiability.
Practical notes on the execution of the experiment
Supercooled water can be most easily obtained during winter at outside temperatures about -5 °C. We pour clear water in a clean PET bottle and leave it outside overnight. It is enough to drop a small piece of ice or a snowflake in it or to slam it to the floor to initiate crystallization. The author used common tap water in Brno and reached a success rate above 90 % during many dozens of tries.
In most cases we cannot rely on the weather and we have to cool water artificially. Unfortunately, common refrigerators and freezers are not of use – the temperature is too high in the fridge and too low in the freezer rendering a high probability of spontaneous crystallization. Cooling with a mixture of saline solution and ice proved itself to be useful. We need about 1 kg of crushed ice mixed with half a litre of chilled water to supercool a 1.5 l of water in a PET bottle. We keep stirring salt in the mixture until it reaches −8 or −9 °C. We put the crushed ice with the PET bottle in a well insulated vessel. If the initial temperature of water in the bottle is close to 0 °C it will be sufficiently supercooled in 30 – 60 minutes. It is an advantage to have a thermometer built in the bottle (see Fig. 2). We can monitor the temperature of undercooling and we immediately get to know when the water unintentionally freezes (its temperature grows fast to 0 °C and stays so for a long time).
The whole experiment must be done as fast as possible to limit warming of the mixture in the bottle so we should prepare everything carefully in advance. One does not manage to pour all the ice through the bottleneck every time and it is necessary to cut the bottle apart. The temperature of the water in the calorimeter just after all ice has melted is a very important parameter that influences the result very much. This temperature is always a little bit above the zero point because it is better to pour some more warm water than necessary in the mixture to speed up melting. The thermometer used for measuring the final temperature must be as precise as possible.
The experiment proceeds as follows. First we carefully take out the bottle from the cooling mixture. The measuring tube is already attached to the bottle. We mark the initial position of the water column in the tube. Then we initiate crystallization by a punch and watch the shift of the water column. We mark its position as soon as it markedly stops or slows down. We do not waste time by reading the position on the scale, we just mark it with a peg for example. We empty the content of the bottle in the calorimeter that has been cooled to 0 °C as fast as possible. We mix warm water in the mixture and carefully look out for the moment when the ice is completely melted. We measure the temperature in the calorimeter for the whole time with an accurate thermometer that was also pre-cooled to 0 °C so that the measuring of the final temperature is as fast as possible. We read and write down required experimental data – the shift of the water column and the mass of used warm water – after the end of the experiment.
Reference
[1] http://en.wikipedia.org/wiki/Nucleation
[1]Usage of Gibbs potential as the thermodynamic potential at constant temperature and pressure would be more proper.
[2] The problem of nucleation is connected not only to solidification but also to boiling or condensation of water steam. Superheated water does not boil for a similar reason as undercooled water does not begin to solidify. Chemists call this state in Czech "utajený var" which means "secret boiling point". Because it means a certain risk in the chemical laboratory, it is commonly avoided by the use of so called boiling chips that guarantee heterogeneous nucleation of steam bubbles.