About paper
Czech originalTwo simple innovative experiments from mechanics
Introduction
Experiment has the same purpose in teaching physics as it has in physics. It is used to verify conclusions or it is the starting point for the research of yet unknown phenomenon. The next two examples are given to emphasize the importance of the experiment in teaching physics, primarily as a way to develop the physical thinking of the students. This is not developed by mere watching of the experiment (observation) but only when the student himself tries to find the answer to WHY the process takes place.
1 Liquid in a vessel (lesson plan)
The purpose of this experiment is to convince the students that a liquid at rest obeys Pascal’s law and that any movement of a liquid is induced by the difference of pressures. It is not always helpful from the didactic point of view to tell the students what we are going to prove with the experiment.
To fulfill the aim listed above the following procedure proved itself worthwhile: first the students constructed and reasoned answers to the asked questions (WHY?) and then in the ensuing experiments proved which answers were correct.
Tools:
PET bottles, a larger basin, beaker, funnel, ruler, a sharp spike or needle (to make holes in the bottles), graduated cylinder, stopwatch, calliper
P1 Empty bottle in water
Q1 What happens when we submerge an empty bottle with two holes (A, B) into water according to fig. 1?
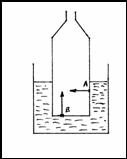
Fig. 1
(Water spurts through holes in the bottle. WHY?
The liquid exerts pressure always perpendicular to the surface of the vessel. F=PA)
P2 Closed bottle filled with water
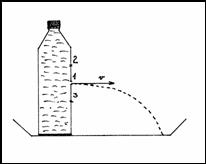
Fig. 2
Q2 What happens when we make hole 1 in the side of the bottle – fig. 2.
(Water does not spurt. WHY?)
Q3 What happens when we squeeze the bottle?
(The water spurts. WHY? - Pascal's law)
Q4 What happens when we make a second hole 2 above the first hole?
(Water spurts from the bottom hole only. WHY?)
Q5 What happens when we make a third hole 3 beneath the first hole?
(Waters spurt only from this hole. WHY?)
E3 Bottle full of water – first closed then open
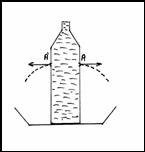
Fig. 3
We fill the bottle with water and close it. We make a hole A. We already know that water will not flow out.
Q6 What happens when we make second (third, …) hole A' at the same height?
(Water will not spurt. WHY?)
Q7 What happens when we open the bottle? - fig. 3
(Water spurts out. WHY?)
Q8 Does the speed of leak change if we squeeze the bottle?
(No. WHY?)
P4 Exercise of calculating the velocity of spurting water and the length of the spurt
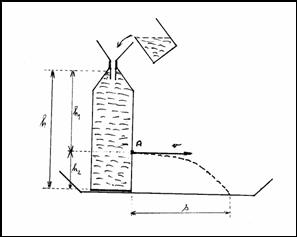
Fig. 4
The hole A is made at 1/3 of the bottle's height and we maintain the surface at constant height h – fig. 4.
In our particular case h = 30 cm, h1 = 20 cm, h2 = 10 cm
We do the required calculations and compare the results with measured values.
Solution:
· Spurting water travels at constant velocity in the horizontal direction – the horizontal distance traveled is: s = vt
· In the vertical direction the water performs free fall: \[ h_2 = \frac{1}{2}gt^2 \qquad \rightarrow \qquad t = \sqrt{\frac{2h_2}{g}} \approx 0.14\,\mathrm{s}. \]
· The speed of spurting water is \(v=\sqrt{2gh_1}\approx 2\,\mathrm{ms^{-2}} \) and s = 28 cm.
(The length of the throw can also be calculated simply from the relation \(s = 2\sqrt{h_1h_2} \).)
· The calculated value of the horizontal displacement of the spurting water is s = 28 cm.
Measured value s = 28 cm.
P5 Horizontal throw analogy to angled throw
The horizontal distance travelled following an angled throw is \[ d = \frac{v^2}{g} \sin 2\alpha \] thus, it is the longest for angle of launch α = 45°. We can calculate and then measure (for example according to fig. 2) in analogy that the length of the spurt of the liquid out of the hole in the middle of the liquid’s height is the longest.
2 Connection to mathematics
We can use these experiments to train mathematical skills. Following are two examples:
a) Euclid’s theorem
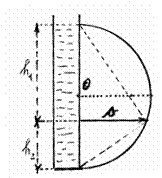
Fig. 5
From the equation for the length of the throw \(s = 2\sqrt{h_1h_2} \) it follows that the length of the throw will be maximal when the square root \(\sqrt{h_1h_2} \) is minimal. From fig. 5 we can write Euclid’s theorem as \(s' = \sqrt{h_1h_2} \) which means that the length of the throw will be maximal in absolute value for h1 = h2 = h/2.
b) Determining the diameter of a cylinder
We give the students a task to calculate the diameter of the hole through which the water spurts out and compare the result with the measured value (for example, by measuring the diameter of the needle we used for making the hole in the PET bottle with a caliper). We advise them to measure the volume of water that has flowed in time τ through the area A of the vessel where the volume of the cylinder is V = Avτ.
The fact that the values will differ can be an interesting topic for an optional extended discussion.
3 Stability of bodies
The stability of bodies is defined by the work required to turn (move) the body from the steady stable position to another position. For turning a body, the decisive factor is not the force but the moment of force. Experience shows that this concept is very difficult for the students.
Solving a particular exercise to determine the stability of the block is helpful to understand both of these terms. To do this, one should calculate:
a) the work W that we need to develop to overturn the block,
b) the forces FA, FB, FK, FT, FL that we must exert perpendicularly to the lever arm at relevant points if the axis of turning is the edge of the slat Z – see fig. 6.
The calculation will show and the experiment will prove the easiest way (easiest rotation axis) for turning the block. The students shall measure necessary data (the mass of the body and its size), do the calculations and compare the outcomes with measured values.
Necessary equipment: ruler, dynamometer, perpendicular triangle, twine, scissors, needle (to indicate the centre of gravity), plumb line.
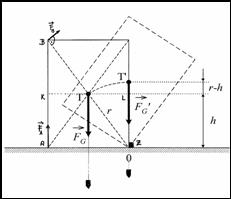

Fig. 6 (left) Fig. 7 (right)
We used a box with dimensions (29,0 × 27,6 × 10,0) cm3 and mass 0,450 kg; instead of a plumb line we used a golf ball on a string that we hung on a needle dug in the centre of gravity – (fig. 7). Calculated results were in good correspondence with measured values: W = 0.68 J; FA = 2.25 N; FB = 1.56 N; FK = FT = FL = 3.10 N.
I am convinced that the students will remember knowledge and skills acquired in this way more easily and more permanently.
Bibliography
[1] JANÁS, J.; TRNA, J. Konkrétní didaktika fyziky I. Brno: MU, 1995.
[2] BEDNAŘÍK, M.; ŠIROKÁ, M. Fyzika pro gymnázia. Mechanika. Praha: Prometheus, 2000. ISBN 80-7196-176-0