About paper
Czech originalElastic or Inelastic Wrecking ball?
In this simple experiment we are trying to overturn a standing block with a pendulum, as if we were knocking down a building. The pendulum consists of a hinge (say, a fixed length of string) and a ball that is either elastic or inelastic. We demonstrate that the same initial deflection (the same initial energy) of the pendulum is sufficient to overturn the block in one case and insufficient in the other.
It is possible to investigate the problem in more detail and to find out, for example, the coefficient of restitution.
The original idea for this experiment comes from the journal The Physics Teacher [1].
Should we smash the door with an elastic or an inelastic wrecking ball?

Fig. 1 – Experimental setup
When we speak about the law of conservation of momentum or about elastic and inelastic collisions in physics, it is interesting to ask the following question: If we throw an elastic ball (a tennis ball) and an inelastic ball (a baseball) of the same weight against a wall, which of them exerts a larger force on the wall? The elastic ball bounces back; the inelastic ball merely falls on the ground. If the students are “too” clever, we can try to confuse them with a theory that the elastic ball is coming back with its initial energy and it probably gave no energy to the wall while the inflexible ball (that gave the wall half as much momentum as the elastic ball) lost all its energy.
To decide between these contradictory opinions we are going to use a simple experiment. We hang the pendulum from two filaments, so that its motion will be planar, next to a block standing on its smallest side (fig. 1) – the pendulum in its vertical position is just touching the block. One side of the pendulum bob is made from an elastic material and the other side is made from an inelastic material (for example, a steel ball half-covered with modelling clay). We can choose whether the collision will be elastic or inelastic by turning the weight – the mass is obviously the same in both the cases. Experience shows that the length of the pendulum should be at least two times greater than the block’s height and that the ball should hit the block in the upper third of the block’s height (very large initial angles of the pendulum are needed with a shorter length string and the measurement is not precise).
If we deflect the elastic pendulum too little, it will bounce back from the block. For angles larger than a certain angle the pendulum knocks the block down. When we turn the weight, we can easily demonstrate that the initial deflection of the pendulum (thus the energy) needed to overturn the block is significantly smaller for the elastic collision than for the inelastic collision.
Mathematical solution of the problem
If we go further, we can see that the issue is interesting also from another point of view. It is a more complicated problem but it can be solved with high-school-level mathematics and physics. Three parts of mechanics meet here – the conservation laws, rigid body rotation, and the problem of stability. Moreover we can do some measurements as a part of laboratory exercises or as an optional extension (see below).
We split the whole process into three parts – the movement of the pendulum (transformation of the mechanical energy), transfer of the angular momentum and the stability of the block.
The pendulum
In the first phase the potential energy of the pendulum is transformed into kinetic energy. We ignore any losses of mechanical energy in this phase. As we know the initial angle and the length of the pendulum we can easily find out the velocity of the ball just before the collision. The law of conservation of mechanical energy in this case is \[ mgl(1- \cos \varphi) = \frac{1}{2} m v^2. \]
The rotational energy of the ball is many times smaller than the energies that are considered in this formula so we neglect it.
Transfer of the angular momentum
After the collision the ball bounces back with a scalar velocity v' that is smaller than the initial (just before the collision) scalar velocity v. The ratio k between these velocities is called the coefficient of restitution.
\[ \frac{v'}{v} = k \]The block begins to move at the same moment. To simplify the issue we neglect the possible horizontal movement of the block and consider only turning of the block. The law of conservation of angular momentum is then
\[mvh = - mv'h + J \omega,\]where h is the height of the collision point, J is the moment of inertia of the block about the axis of rotation that goes through its bottom edge and ω is the angular speed of the block immediately after the collision. The term with v' has a negative sign – the velocity v' is in the opposite direction to the initial velocity v. All the moments in the last equation are related to the axis of rotation of the block. From the last two equations we get \[\omega = \frac{mvh(k+1)}{J}. \]
The stability of the block
In order to overturn the block the centre of mass must be moved over the point of rotation, so it must be elevated from the height a/2 to the height \[ \frac{u}{2} = \frac{\sqrt{a^2+b^2}}{2}.\]
The change of potential energy during this elevation must be matched by the initial kinetic energy of the block Ek. We formulate this condition of overturning as \[ E_k \geq \frac{Mga}{2} \left( \sqrt{1+\frac{b^2}{a^2}} - 1 \right) .\]
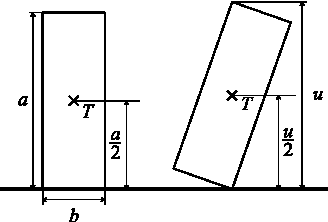
Fig. 2 – Overturning of the block
The initial kinetic energy of the rotation of the block is expressed as \[ T = \frac{1}{2}J \omega^2 = \frac{\left[mvh(k+1)\right]^2}{2J}. \]
We can find the moment of inertia \[ J = \frac{M}{3}(a^2 + b^2) \] in physical tables or we can find it following Steiner’s theorem or we can calculate it by integration.
And everything together yields…
We know all the masses, dimensions and lengths in our case. We can find the minimum initial angle of deflection of the pendulum needed to overturn the block. The only unknown value is the coefficient of restitution which says “how elastic is the collision”. After some algebraic calculations we get for the coefficient of restitution a long equation \[ (k+1)^2 = \frac{1}{6} \frac{(a^2+b^2)\left( \sqrt{1+\frac{b^2}{a^2}} -1\right)}{h^{2}(1-\cos \varphi)} \left(\frac{a}{l}\right) \left(\frac{M}{m}\right)^2.\]
Theory versus Reality
I used a particle board and a steel ball, half-covered with modelling clay, mentioned above. I performed a larger number of experiments with various pendulum lengths (the longer the pendulum, the smaller the minimum angle). The experiments were recorded with a video camera and then evaluated. It was easy to measure both the minimum initial angle and also the angle that the pendulum rises to after the collision on its way back toward the initial position. Thus, it was possible to determine the coefficient of restitution in two different ways.
Measurements were made for angles up to 70°. The correspondence is good for elastic collisions and small angles (up to 30-40°) – both methods yield a coefficient of restitution of approximately 0.75; the uncertainty is about 0.1. For angles larger than 40° the calculation of the coefficient of restitution from the minimum initial angle yields systematically larger values (about 0.7) than the coefficient of restitution measured from the recording (0.6-0.5). This can be justified by the fact that the pendulum is not ideal – it can be seen that the pendulum does not reach the initial deviation even if it swings without a collision.

Fig. 3 – Measuring of the limiting angle on a picture from the video recording
For inelastic collisions the calculation from the minimum initial angle yields a coefficient of restitution of (0.24 ± 0.3) and this value increases for larger initial deviations of the pendulum. The minimum initial angles are in this case 15° larger than for the elastic collision performed under the same conditions. The method of direct measurement of the coefficient of restitution from the video recording does not work well in the case of the steel ball half-covered with modelling clay because the clay layer is not spherical and the pendulum is bouncing back in different directions and a lot of energy is lost.
Hints for measurement
Attention should be paid to some technical issues if we want to get out of the experiment more than the mere fact that the elastic side of the pendulum knocks the block down more effectively than the inelastic side of the pendulum. In particular:
• The underlying floor/table should be horizontal.
• The block should be prevented from horizontal movement so that it is purely overturning (by, for example, a skewer glued on the floor or two pins at the edge of the block).
• The block must really be a rectangular parallelepiped. It tends to fall in other directions when its edges are not rectangular. This seems to be the most difficult condition to meet.
• The pendulum should hit the block at the lowest point of its trajectory, perpendicularly to the block and at the block’s vertical center line (in the middle of its width). The efficiency is lower, the minimum initial angle is larger and the pendulum tends to rebound erratically if this condition is not met.
• If you decide to record the experiment, you need to aim the camera very precisely perpendicularly to the plane of swinging.
If you want a more perfect pendulum, it is possible to buy a set of two black balls of the same appearance but with very different elasticity from the online shop of Arbor Scientific [2] for the price of approximately $4. You can cut the balls in half, put a string between one of the elastic half-spheres and one of the inelastic half-spheres and glue them together. You get a ball that looks homogeneous but has different elasticity on opposite sides.
Bibliography
[1] Micklavzina S.: Impulse Demonstration Using a 'Half-Bouncy' Ball, The Physics Teacher, Vol. 34, no. 4, p. 253, April 1996
[2] Arbor Scientific, Happy and unhappy balls [http://www.arborsci.com/detail.aspx?ID=362]