About paper
Czech originalPhysics with The Laughing Cow – or experiments with very simple equipment
This contribution describes physical experiments with very simple tools made of round cheese paper boxes.
Introduction
Many of the previous reports from the Fair of Inventions have shown that a physicist or a physics teacher can utilize absolutely anything to do experiments: a PET bottle, coins, contents of a first aid kit, CDs and God knows what else.
A spinning top made of a half of a round processed cheese box is useful for many experiments. The axis of the top can be made from a sharpened skewer. The centre of the box can easily be found by balancing the box on a pin. We glue the skewer and the box together with hot glue. (See Fig. 1) It is only necessary to glue the skewer perpendicularly so that the spinning top rotates steadily. Then, we can begin experimenting.
Mechanics experiments
Angular frequency – measurement with a computer
The top is spinning quite fast on a solid surface. How fast can we actually spin it with our fingers? Our eye can not follow the rotation, much less count the turns… A computer can help us. A phototransistor connected by a cable to the microphone input of a computer can detect changes in lighting. If we draw a mark on the spinning top with a pencil and put the phototransistor near that place, we can measure the frequency.
We can either record the signal and evaluate it with a program such as Adobe Audition, or evaluate it directly, for example with the freeware program SoundCard Oscilloscope. The result is shown in figure 2. The total time shown is 1 s. We can easily see that the top is spinning about 17 times per second. The software mentioned above is capable of measuring the time between two impulses even more precisely. (The frequency in this case was 17.4 Hz.)

Fig. 1 A top made of a processed cheese box
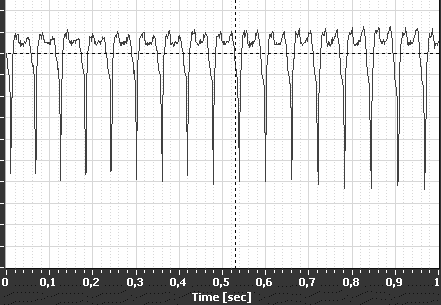
Fig. 2 The phototransistor signal of a spinning top
Angular frequency – A very simple measurement
How can this same measurement be done without a computer and a phototransistor? An approximate measurement can be made by merely placing the axis of the top horizontally at the edge of a table. The axis travels along the edge – we can easily calculate the frequency from the distance travelled in 1 s. (This consideration can help some students to understand the difference between angular frequency angular velocity.) We can prevent the slipping of the axis if we put on it a piece of rubber from a bicycle valve obtained in a bicycle shop. This measurement is quite imprecise but we can use it to determine the frequency up to 20 revolutions per second.
The spinning top or “almost a loop of death” (unusual gravitational acceleration gauge)
Put a lightweight object (a piece of a skewer, a little screw-nut or a paper clip) on the top and spin it with your fingers. The object moves towards the circumference, of course. If you turn the axis to the horizontal position (the top is still spinning), the object will remain at the circumference even if it is in the highest position. Voila, you have a model of a carnival attraction – a vertical loop in which you can sit upside down without falling down from your seat – or almost a model of the “loop of death”.
As the angular frequency decreases there comes a moment when the object falls out of the top. (We probably would not like to do such an experiment at a carnival.) It is surprising that it happens at a relatively low frequency of less than 2.5 revolutions per second. We can calculate the gravitational acceleration which must be just equal to the centrifugal acceleration at that moment. If we measure the angular frequency with a computer as described above, we can achieve an accuracy of almost within 10 %.
The spinning top as a centrifuge (or rotating system put in praxis)
We can use our spinning top as a simple centrifuge. It is interesting to realize that a very high value of centrifugal acceleration can be achieved when spinning the top at relatively low frequency. If we spin the top with our fingers (17 revolutions per second as mentioned above), the angular velocity ω reaches the value of 100 rad s-1 and the acceleration at the circumference (r = 5 cm) is more than 500 m/s2. It is more than 50 g in terms of gravitational acceleration!
We can reach even higher values of angular frequency if we fasten the top to an electric drill or connect it to an electromotor. A small modeler’s drill can achieve 6 000 revolutions per minute. It means 100 revolutions per second and angular velocities higher than 600 rad s-1. Now calculate the acceleration at the circumference of the box! A dry formula rω2 is much more interesting if it yields a result of almost 20 000 m/s2 or 2 thousand g! It means that every gram develops the same force against the circumference as a two-kilogram weight at rest.
We can demonstrate the effects of such a big centrifugal force if we put two little pieces (like a cube of about 1 cm3) of processed cheese at opposite sides of the box (to maintain the balance of the top). In this case it is not enough to spin the top with fingers alone, although only 40 revolutions per second are enough to spread the cheese into a thin layer. I recommend covering the interior of the box with some tape (so that the cheese can be removed after the experiment) and closing the box with the cover (otherwise we will see the cheese joyously flying away in every direction). It is recommended to control the other end of the axis with your fingers to prevent vibrating of the centrifuge.
Precaution: Do not put any solid objects, not even nuts or paper clips, into an open centrifuge (and not even a closed one) driven by a motor or a drill! It is, however, an opportunity for a discussion with your students: at 100 revolutions per second the peripheral velocity is more than 30 m/s, which is more than 100 km/h. Does anybody want to be hit in his forehead or eye by a nut with such velocity? Make sure that nothing can leave the box at any time (it is good to stick together the ends of the paper strip which forms the circumference of the box with tape). We recommend not trying to spin the top at higher frequencies even though some drills can achieve them. 18 thousand revolutions per minute would mean centrifugal acceleration of 170 thousand m/s2 and peripheral velocity higher than 300 km/h. It could be interesting to argue that in that case a piece of cheese would develop the same force as if a burly sumo wrestler stood upon our foot, but it is not worth the danger.
A little bit of oscillating
Torsion pendulum
We can easily turn our spinning top into a torsion pendulum. Just put a bicycle valve rubber at the end of the skewer axis of the spinning top. If you hold the other end of the rubber between your fingers and spin the top with the other hand, you can see a nice example of torsion deformation of the rubber. The rubber slows the spinning of the top down and then makes it spin backwards. The period of this oscillation was 2.9 s for an 8 cm long rubber piece and a typical paper cheese box.
Measurement of the moment of inertia
We can do an experiment to measure the moment of inertia of the box J0. If we add a reference object with known moment of inertia JP to the box and measure the period of torsion oscillation T1 of the box with the object and the period of torsion oscillation T of the box by itself, the moment of inertia of the box is: J0 = JP/((T1/T)2 –1).
The slices of processed cheese from the box can serve us as reference objects. The inscription on the box states that 8 pieces of cheese weigh 140 g. The mass m of one piece is thus 17.5 g. The moment of inertia of a slice is given by the same formula as the moment of inertia of a cylinder (½mr2) because it is a cylindrical section. Our measurements and calculations yielded a value of J0 = 2·10-5 kg·m2 for the bottom part of the paper box with a skewer.
Resonance
We can also demonstrate resonance using this torsion pendulum. If we swing the upper end of the rubber piece at a very moderate amplitude at the proper frequency, we can achieve very strong torsion oscillation of the box. Faster or slower swings do not make the box oscillate.
A little bit of acoustics
Savart’s and Seebeck’s sirens – and one other
The box works as a siren (not too loud) if we cut out periodic notches in the perimeter of the box. When we rotate the box with a drill or an electric motor and touch the notches with a stripe of paper, we have a Savart’s siren. When we blow at the notches with, for example, a straw, we have a Seebeck’s siren.
Another quite unusual possibility is to sample the light coming through the “teeth” at the perimeter of the box with a phototransistor. We can analyze the signal with a computer (and analyze for example its frequency) but we can also amplify and reproduce it.
One optics experiment
Cylindrical mirror
A strip of shiny foil on the inner wall of the box works as a cylindrical mirror. The sun is a perfect source of collinear light for visualization of the trajectory of the rays of light. (See Fig. 3 and 4).

Fig. 3 A wide beam of light showing aberration of a cylindrical mirror

Fig. 4 A narrow beam of light is being focused into the focal point of the mirror
Something for astronomy
Sundial
The top works as a sundial if the skewer is positioned parallel to the axis of the Earth. We can surround the outside of the box with a strip of paper with hour marks (see the figure below). One hour corresponds to 1.5 cm at the circumference of the box thanks to the providential diameter of the box. (If it does not correspond well, we can easily put another strip of paper between the box and the hour strip.) The length of the skewer that should be sticking from beneath the box to provide the appropriate angle of the axis is a good question for the students to answer.

A little bit of theory or order of magnitude comparison
It is illustrative to consider the sizes of some very big and very small objects in comparison to some common object from daily life. Let us use our box!
A hundred million times enlarged cheese box would be roughly the diameter of the Earth. (The inaccuracy is about 20%)
A billion times miniaturized cheese box would have nearly the size of an atom. (We would get Bohr’s radius with error no larger than 5 %.)
And finally another comparison: the cheese box as the trajectory of the Earth around the Sun. (The scale is 1 : 2.7·1012.) The diameter of the Sun would be 0.5 mm; the diameter of the Earth would be about 5 μm; the diameter of the orbit of Jupiter would be less than 60 cm and Neptune’s orbit diameter would be 3.3 m so this model just fits inside a classroom…
Finally, a little bit of “pyramidology” ☺
Many people are trying to look for the mysteries of the universe among the dimensions of the Great Pyramid of Giza. But why should we bother the Pyramid? Let us use our Laughing Cow box! Do not hesitate to marvel that we can get the following:
The ratio between the diameter of the box (11 cm) and its height (2 cm) raised to the fourth power times 2 yields 1830 – it is almost the ratio between the weight of proton and electron (1836.152663). If we take for the value of the diameter of the box a more accurate value 11.111111 cm and a more precise value of the height 2.018542011 cm we get it exactly! After all, the pyramidologists also adapt the dimensions a little bit …
The calculation of this constant is even simpler if we combine the box with the Pyramid. The height of the Great Pyramid (146.7 m) divided by the height of the box (2 cm) gives after another division by 4 the value 1833.75. If we press the box just a little bit, we get the exact value again. J
Similarly we can obtain the values not only of other physical constants but also of mathematical ones. The diagonal of the base of Cheops’ Pyramid (232.4×√2 m) divided by the diameter of the box (let us say the inner diameter 11.025423 cm) raised to the 1/8-th power yields the value 2.718281…, which is e.
Add a mysterious face, mumble some cryptic words during these calculations – and if there was not a cheese box in it, somebody could even think that you are serious… If your students will ever try to explain you what can be read from the dimensions of the pyramids, you can show them that even the Laughing Cow can tell us something seemingly interesting. It might bring them to a little bit more rational and critical point of view.
Yet we must not forget an absolutely undisprovable “blockbuster”. The circumference of the box divided by its diameter yields 3.1415926… - really, it is π!
Conclusion
And is that all? Not even close! Only considerations of space limit us from describing even more ideas. We haven’t touched electricity and magnetism, for example. So maybe see you some other time at Physics with the Laughing Cow II.
And if this text has brought you some inspiration, it fulfilled its purpose.