About paper
Czech originalA Bit of Optics at Home
Abstract: This contribution introduces some suggestions on simple experiments from geometrical optics. They can be realized at home with usual kitchen equipment. They are intended to increase the interest in physics and to eliminate the unwanted form of mechanical learning of optics.
Refractive Index Measurement
There follow descriptions of two simple home-made measurements of refractive index.
Measuring of Refractive Index Using an Immersed lamella
We need a vessel that has at least one transparent side. It can be a perspex or glass sugar container for example.
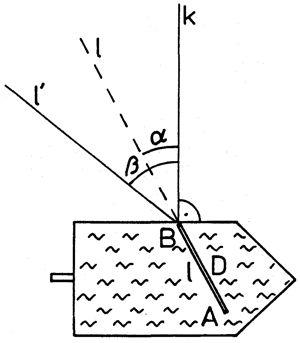
Fig. 1
We pour water into the container and then we partially immerse a plane lamella D into the water vertically but not perpendicularly to the side of the container (Figure 1 shows the situation from above).
If we look at the lamella through the side of the vessel, we can see that the immersed part of the lamella seems to be oriented in another direction than the upper part of it.
A more detailed analysis shows that the apparent direction l’ of the immersed part of the lamella, the direction l of the upper part of it and the direction k perpendicular to the side of the container show the angle of incidence α and the angle of refraction β. A light beam that travels horizontally through the water along the immersed part of the lamella refracts to the air in the direction of the apparent orientation of the immersed part of the lamella. This very refraction of light induces the apparent reorientation of the lamella below the water surface.
For better evaluation of these effects, we put a sheet of paper on the table below the container so that we can mark the directions of water-air interface (we neglect the thickness of the container’s side), the perpendicular to the side k, the real and the apparent direction of the lamella (or the direction of the incident (l) and the refracted (l’) light beam). We measure the angles of incidence α and refraction β for several positions of the lamella and calculate the refractive index of water (from the law of refraction) as the average of individual measurements. From the formula v = c/n we can also calculate the velocity of light in water.
Measuring of Refractive Index Using the Shadow
The refractive index of water can also be measured in a kitchen sink. Put a can of juice into the sink (or in a wide vessel) in upright position (Fig. 2). Shine at the can with a light source that makes a sharp shadow (the Sun, a light bulb without lampshade). Mark the length of the shadow of the can on the bottom of the empty sink. Hold the can with your hand in place and fill the sink with water so that the top of the can is a little bit below the surface of water. Determine the length of the can’s shadow in this situation. Explain why the shadow has shortened. Find out what other data will be necessary to calculate the refractive index of water. Measure them and calculate the refractive index of water from the law of refraction.
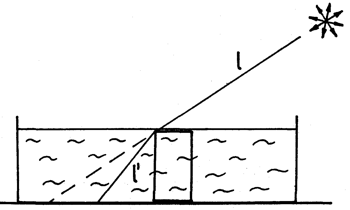
Fig. 2
Total Refraction
A Mysterious Circle on the Sink Bottom
Total refraction on the interface water-air can be demonstrated in an experiment with a small shining light bulb (4,5 V) immersed below water (Fig. 3). It does not damage the bulb and no electric insulation of the conductors’ contacts is needed. This experiment can be made in a kitchen sink.
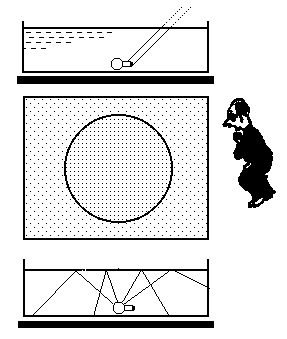
Fig. 3
A part of the light emitted by the light bulb comes back on the bottom of the sink after it reflected on the water-air interface. There can be observed an interesting circular area on the bottom of the sink – the exterior of the circle is illuminated more intensively than its interior. It seems to be a paradox.
The explanation of this paradox lies in the phenomenon of total reflection. The light beams that fall on the on the water-air interface under angle of incidence that it lower than the critical angle are not reflected totally and a part of their intensity comes out of water into the air. Thence the area inside the circle is illuminated less intensively. On the contrary, the area outside the circle is illuminated by the beams that reflect totally (beams that fall on the air-water interface under angle of incidence larger than the critical angle) receives larger intensity of illumination. If we measure the radius of the circle, the depth of the bulb below water and the height of water in the sink, we can calculate the refractive index of water relative to the refractive index of air.
We can also observe the dependence of the radius of the circle on the depth of the bulb below water. The circle can disappear for higher depth of the bulb because the circle is so large that it does not fit in the area of the sink bottom.
We can see that the physical laws are no strangers to our kitchen environment. They are ready to show off their tricks even in the kitchen sink in our worktop.
More Experiments
The Shadow and Mystery of the Moon
It took plenty of time for people to understand the laws of motion of celestial bodies, and even the Moon. It is surprising that they did not realize that the Moon is a spherical body and that its lighting area is formed by the sunlight reflecting from its spherical shape.
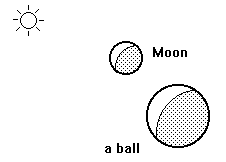
Fig. 4
But it is very simple. The shadow occurs thanks to direct propagation of light. Let us see it in an experiment (Figure 4). Take a ping-pong ball in your hand in the daytime when you can see both the Sun and the Moon. Stretch your arm forward nearly in the direction of the line between your eye and the Moon. What can you see? The little white ball in your hand is illuminated exactly in the same way as the Moon and it will show the same phases as the Moon. The only difference is that it cannot be observed during the night because our hand is too short to put the ball out of the shadow of the Earth.
Experiments on the Side of the Fridge
We can observe the laws of reflection of light also on the side of a fridge. First we will need a light beam. We can use a lamp or a flashlight placed on the top of the fridge so that the bulb protrudes above the side of the fridge. We put a shade with a slit below the light source and there emerges a light beam on the side of the fridge. The shade can be made from paper or we can form the slit by two books lying next to each other.
To study refraction of light on the side of the fridge (Figure 5) we use a sugar container made of perspex or glass again. We put some water in it and place it in the path of the light beam. If the angle of incidence of the beam is not perpendicular to the air-water interface, we can observe an angle of refraction that is smaller than the angle of incidence.
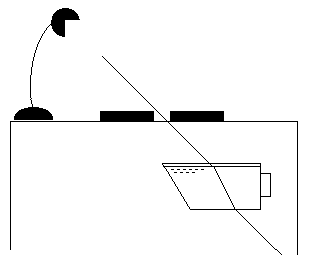
Fig. 5
In the next experiment we use a water prism in a tilted sugar container. We observe a change in the direction of travel of the beam or “deviation” of the light beam (Figure 6). The measure of declination depends on the angle of refraction of the prism which is the angle between the bottom of the container and the water surface. It can be changed by tilting of the container.
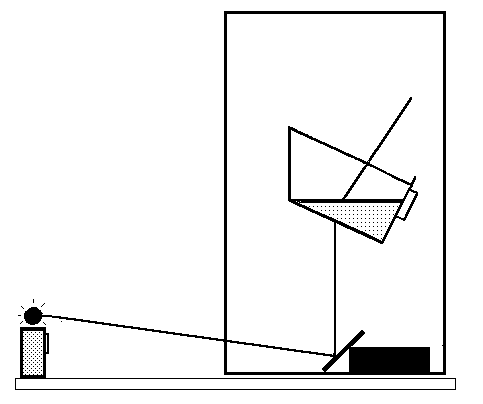
Fig. 6
We can mark the directions of the beam’s travel with a washable marker and analyze the two refractions that took place in the experiment. We mark also the lines perpendicular to the surfaces and measure the angles we are interested in.
The beam that travels through a plan-parallel layer of water (for the container placed horizontally) does not change the direction of its travel but it moves aside thanks to twofold refraction of light on two parallel interfaces of water.
This side-shift of the beam can also be observed with a Tic-Tac box filled with water and fixed on the side of the fridge with magnets (Fig. 7).
The same effect can be studied on a table without a special light source. We draw a line on the paper and watch it through a Tic-Tac box filled with water. The line seen through the block of water is shifted aside depending on the inclination of the box. We can measure the side shift of the line and the angle of the box’s inclination and calculate the approximate refractive index of water.

Fig. 7
References
[1] Baník I., Baník R.: Kaleidoskop učiteľa fyziky. MC Bratislava, 1992-2000