About paper
Czech originalNot all methods of weighing are equal
Abstract
This paper deals with some exotic manners of weighing that facilitate the development of physical ideas. They can be used for determination of mass density using household appliances and other tools.
Introduction
Determination of the mass of some convenient object without using any specific technical instruments (such as weights) is a good theme for developing physical and creative thinking concerning the choice of methods and instruments.
Experiments for the youngest ones
The already mentioned problem has begun to be up-to-date especially in the case of the youngest students, when the most appropriate method of weighing seems to be the use of a ruler and some coins. We can use the ruler as a double lever which is supported at the centre of gravity by a pencil with circular cross-section. If we know the mass of the coin, we can determine the mass of a rubber, a key, a pencil sharpener and many other small things. It is also possible to determine the mass of a light porous sponge and after measuring its proportions, you can also calculate its density. The density of the rubber can be evaluated by the same procedure.
It is obvious that when you are balancing two objects of different masses, the shorter arm of the ruler belongs to the heavier object and vice versa. If you are not an adult but a child, this fact is not so clear- the experiences of life are being gained step by step. It could be cleared up by an experiment in which a coin on one side of the ruler is replaced by two coins, but the one on the other side still stays in its place.
Using the mass of the coin, the child can determine the mass of the rubber as well (with a little help from the parents). The ruler with the coin (which has been placed on it) is overlapping the edge of the table. Pull the ruler until it reaches the critical state in which the system is unbalanced and rotates around the edge of the table. The mass of the ruler can be estimated using the term describing the balance of the system (force moment), considering the role of the centre of the gravity and the weight of the ruler. If the mass of the ruler is known, it is also possible to determine the masses of the other objects. It is a way to verify the results of the previous measurements.
Measuring the mass by the method of a two-equation system
The previous experiments can be repeated with a slight modification-we can use a board and a piece of chocolate instead of the ruler and coin, respectively. Such an experiment is illustrated in fig.1.
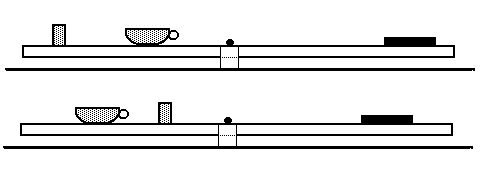
Fig. 1
Balance the three solid objects on the board which is secured by an elastic band to the pencil that supports it on the centre of gravity. Only the mass of the one object is known (the piece of chocolate), the masses of the remaining ones (the cup and the glass) are unknown. Balance the system by moving the piece of chocolate. The task is to determine the masses of these two objects. The case which is illustrated in fig.1 gives us only one equation for two unknown quantities. To determine the masses of both objects, two equations describing two different displacements of objects on the board are required. The analysis of the problem is extremely interesting and educational. The convenient variables x and y represent the two unknown masses; related terms quantify the moment arms. The term describing the mass of the chocolate and the length of the arm is on the right side of the equation. The second formula differs from the previous one only by the coefficients on the left and right sides. We can easily solve the system of both equations and determine the unknown masses. Unfortunately, there are some exceptions that we would like to explain in detail. If both moment arms of force in the second equation were half the value of those in the first equation, the system would not be independent and the solution would not be unique. On the other hand, if the left sides of the equations were equal and the right side of the second one contained the wrong coefficients, the system would have no solution. These considerations about balance can help students obtain a better understanding of mathematical problems that are connected with the system. In general, one can consider a similar method for weighing the three objects.
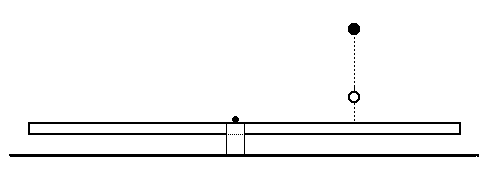
Fig. 2
The impulse method
Fig. 2 illustrates the origin of the ‘impulse’ method of weighing a ball which is dropped from a certain height onto the balanced board. The ball bounces off the board to a height which is lower than before. Using the values of both heights, the change of the ball’s velocity can be calculated. This change of velocity is also connected with the change of momentum. For our purpose, only the change of momentum with respect to the board’s axis of rotation is interesting. If the system is isolated, the change of the ball’s momentum has to be the same as the change of the board’s momentum. The board is oscillating as a physical pendulum and the amplitude of this oscillation determines the starting velocity of the board after the impact. Knowing its mass and the moment of the inertia, the angular momentum can also be estimated. Newton’s First Law of Motion (Law of Inertia) gives us the relation from which the mass of the ball can be calculated. This method does not consider the weighing in its essential meaning but shows us an interesting physical context which gives us nice and useful exercises suitable for lectures of mechanics at the college.
Measuring the density
Fig. 3 demonstrates the measurement of ferrites density by the method of weighing in the air and the water, respectively. Use the ruler whose mass was determined before. Place the ruler into the critical position in both cases, when it is just about to turn at the edge of the table and measure the moment arms of force. The critical position, which is different in each case, gives us the starting point in measuring the ferrites density. In the same way, the density of the ceramics from which a coffee cup is made can be determined.
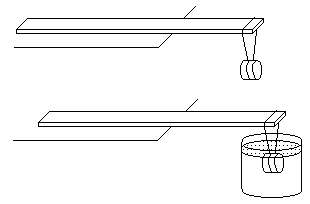
Fig. 3
Fibre weights
Another method of weighing, fibre weights, is shown in fig.4. These weights are constructed with use of the edge of a table, two books and some cotton. A piece of chocolate is hung vertically on the one fibre, and the object to be weighed is hung on the other one. The fibre between the objects has to be tight and mounted in the horizontal position. It is possible to move the books if necessary. The analysis of the problem is very suggestive for the students.
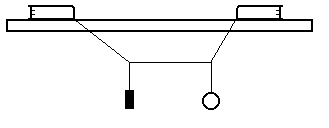
Fig. 4
Weighing with the help of low pressure
Fig. 5 exhibits some quite curious and exotic weighing bowls. The bowl is kept above the surface by a funnel which is turned upside-down. We are creating the low pressure by mouth, which is measured by the pipe. If we measure the critical height of the water column when the bowl falls away and also the area of the circular slot by which the funnel is in the contact with the bowl, we are able determine the mass of the bowl. This measurement is only estimation, but thinking about the solution is interesting.
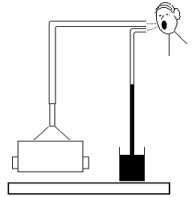
Fig. 5
Weighing with use of the buoyant force
One of the educational methods of weighing is illustrated in fig.6. The bowl with the water (the flask) is placed on the scale and the empty bottle is sunk inside. Regard the change of the weight as measured on the scale. The deeper the bottle is immersed, the bigger is the measured value displayed on the scale. This is the reaction to the buoyant force that is acting on the bottle. The buoyant force increases with the increasing volume of the immersed part which leads to the appropriate reaction.
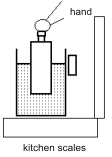
Fig. 6
Weighing with a board
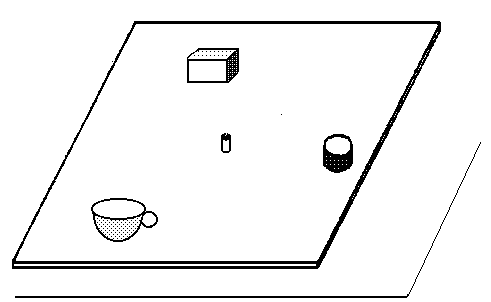
Fig. 7
Weighing two objects with the use of a board is illustrated in Fig. 7. The board is supported at its centre of gravity; two objects of unknown masses are placed on it. We balance the board using an object of known mass. Two equations can be derived from the condition of balance: the first one is resulting from the condition of balance with respect to the axis passing through the centre of gravity and the second one is the consequence of similar condition for another axis (one which is perpendicular to the first axis). If the special case occurs and the all three objects lie on one line passing through the supporting point, it is impossible to determine the masses of both objects simultaneously.
Weighing with a piece of chocolate
Fig. 8 shows a different system for weighing, which is useful especially for the youngest students. A piece of chocolate is used as the weight of known mass. After measuring the mass of the ruler, the force distribution can be determined.
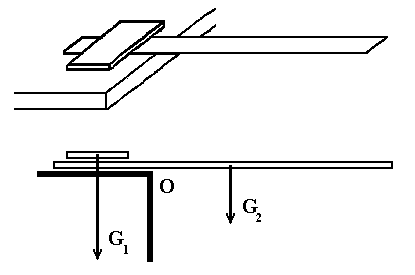
Fig. 8
References:
[1] BANÍK I., BANÍK R.: Fyzika netradične – Mechanika, Alfa, Bratislava, 1990.
[2] BANÍK I., BANÍK R.: Kaleidoskop učiteľa fyziky 1-10, MC Bratislava, 1992-2000.