About paper
Czech originalUnusual measuring instruments 4: Measuring short time intervals
Abstract
A simple device for measuring short time intervals using the charging process of a capacitor is described. It can be used at school to motivate students to investigate the behaviour of an RC circuit. The range of the device is from tens of microseconds or less to seconds or more. The measurement of the duration of a hammer blow on the anvil is described as an example.
Introduction
This contribution is part of a series of articles with similar themes (see for example [1]) that have been presented at the “Fair of Inventions” in previous years. This is once again a suggestion of an experiment or series of experiments that can be used in a high school and possibly also at some optional physics circle at a secondary school. The main experiment was tried out at the Summer Workshop for Teachers College Students in Malá Hraštice (see [2]) in May 2004.
Motivation: a hammer blow on an anvil
If we strike an anvil with a hammer, the hammer rebounds. Yet the hammer was in contact with the anvil for a certain time. How long did this contact last? In other words: What was the duration of the blow?
Fig. 1 The hammer blow on the anvil
We can introduce this problem to the students either separately or in the chapter of mechanics that deals with the relationship between force and the change of momentum in time. If we know the momentum p of the hammer before the impact and assume that 1) the collision is elastic and 2) the anvil is much heavier than the hammer, then the force of the blow is equal to F = Δp / Δt = 2p / Δt where Δt is the duration of the blow.
The duration of the blow seems to be “unmeasurably short” if we watch it with the naked eye. The younger generation of students will not be surprised that it can be measured with a computer, for example with the ISES system. (The sound card of a computer with a proper program can also be used.) We connect one lead from the measurement expansion card to the anvil and the other lead to the hammer. All these elements are then put into a serial circuit with a resistor and a battery. The current flows through the circuit as long as the hammer and the anvil are in contact. The time evolution of the current can be displayed on a computer and the duration of the blow can be measured. This arrangement has typically been demonstrated at mechanics lectures for 1st year students at the Faculty of Mathematics and Physics of Charles University for the last few years.
Can it be done without a computer? We will see that the answer is yes. Moreover, we will be able to measure time intervals even shorter than a hammer blow. (Such intervals can be indistinguishable for some computer measuring systems.) And furthermore our experiment is a nice motivation for the study of capacitors and RC circuits. Our device is not a “measuring instrument”, in fact. It is nothing more than several elements connected together. And it can be made on a shoestring budget.
A Simple measurement – and some calculations for intermediate students
Our measurement makes use of the charging process of a capacitor. The capacitor is initially uncharged. The contacts A and B are connected to the hammer and to the anvil (see Figure 2). The capacitor will charge through the resistor R as long as the hammer is in contact with the anvil. We can determine the duration of the blow from the final voltage across the capacitor.
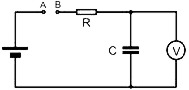
Fig. 2 An RC short time measurement circuit
The whole process can be described with just the knowledge of mathematics and physics from the first year of university studies. If Ub is the voltage across the capacitor and U is the voltage of the battery, then the current that flows into the capacitor is I = (Ub −U)/R. (We neglect the current that flows through the voltmeter.) The charge Q which is stored in the capacitor grows in the time interval Δt by an amount ΔQ = I·Δt and the voltage across the capacitor increases likewise ΔU = ΔQ / C = (Ub−U)·Δt / (R·C). After dividing by Δt we get a nice differential equation dU/dt = (Ub−U)/(R·C) in the limit Δt→0. The solution of this equation under the initial condition U(t = 0) = 0 is U = Ub·(1−exp(−t/T)) where the time constant is T = RC. The time of charging calculated from the final voltage across the capacitor is t = –T · ln(1–U/Ub).
This is a university-level description of the relation between the time t and the voltage U. This derivation can also be presented with a more detailed commentary to high school students who are more interested in physics, to show them the usefulness of differential equations in physics. Luckily, “normal people” can do without these equations.
Ultimately simple calculation
The time-voltage dependence gets markedly simpler if the voltage U across the capacitor is significantly lower than the voltage of the battery. The current I flowing into the capacitor is practically constant in time in this case. Thence the charge on the capacitor and its voltage grows linearly in time.
Let us look at a particular example: we charge the capacitor with a 4.5 V battery through a 4.7 kΩ resistor. The current which flows into the empty capacitor is about 1 mA. It represents a charge of 1 microcoulomb in every millisecond. (ΔQ = I·Δt = 10-3A · 10-3 s = 10-6 C)
The voltage across a 100 μF capacitor grows by 1 μC/100 μF = (1/100) V = 10 mV in each millisecond. (ΔU = ΔQ / C = 10-6 C/10-4 F = 10-2V). 10 millivolts of voltage across the capacitor means 1 millisecond of contact, 1 millivolt means one tenth of a millisecond.
With these particular elements we simply divide the voltage in millivolts by ten and we get the contact duration in milliseconds. We can measure time intervals to a maximum of tens of milliseconds if we settle for an error of several percent. The comparison with the exact equation shows that the error is lower than 5 % for a 40 ms interval.
The resistance of the voltmeter and other influences
We considered the resistance of the voltmeter as infinite until now. But the capacitor does slowly discharge through the resistance RV of the voltmeter. What is the influence of this effect on the measurement?
Today’s hand-held digital multimeters which can be used for the measurement typically have an internal resistance of 1 MΩ. The time constant is T = RVC = 100 s for a 100 μF capacitor. It yields a 1 % drop of the voltage in every second. If we read the voltage in a few seconds after the blow of the hammer on the anvil, the error is a few percent.
We can utilize the discharging process of the capacitor to calibrate our instrument. A capacitor of 100 microfarad is most likely an electrolytic capacitor – and the real capacitance of this type differs very often from the value given by the manufacturer. (It is usually higher.) If we want to measure the time intervals more precisely, we must determine the actual capacitance. We can measure the time after which the voltage is e times smaller than the initial value, for example. This time T is equal to the time constant RC from which we can easily obtain the capacitance C.
Another problem related to the electrolytic capacitor is its discharging time. The dielectric inside the capacitor remains partially polarized after a quick short-circuiting of the capacitor. The voltage of an electrolytic capacitor that was charged to the full voltage of the battery and then short-circuited to zero grows slowly even if it is not connected to any source of voltage. So do not forget to discharge the capacitor for a sufficient time before every measurement. We must also be aware of the polarity of the electrolytic capacitor. The usual modern electrolytic capacitors have a mark on the negative pole which must be connected to the negative pole of the battery.
Other suggestions
Just briefly:
• If we do not want to use an electrolytic capacitor, we will have to work with a capacitance lower than 1 μF which requires a voltmeter with much larger internal resistance. This condition can also be met if we use an operational amplifier, for example.
• We can also use the operational amplifier to construct an “integrator”. The time evolution of the voltage is then linear even for higher voltages.
• A larger capacitance C or resistance R is required for measurement of longer time intervals such as reaction times. We must reduce C or R to measure shorter time intervals.
• Other short time intervals that can be measured are, for example, the duration of the blowing of a fuse or the delay between the ruptures of two thin wires which can be used instead of a photogate to measure the velocity of some object.
• And a last note about the experiment with the hammer and the anvil: The duration of the blow is about one millisecond or less. If we put a nail on the anvil and strike its head sideways, the blow lasts (more than ten times) longer. The duration of the blow is even longer if we strike something really soft, such as a piece of tin.
Conclusion
The advantage of this measurement is among others its cheapness. A resistor costs a few pennies, a capacitor costs about one dollar and a simple multimeter is about $10.
References
[1] Dvořák, L. Netradiční měřicí přístroje 3. In: Sborník z konference Veletrh nápadů učitelů fyziky 8. JČU České Budějovice 2003, s. 131-137.
[2] http://kdf.mff.cuni.cz/Hrastice
The seminar that is mentioned in this text was financially supported by Grant B1828/2004 of the University Development Fund, „Rozvoj aktivizujících forem práce ve vzdělávání učitelů matematiky a fyziky“; and by the Development Project of the Ministry of Education, Youth and Sports of the Czech Republic Number 368, „Heuréka II“.