About paper
Czech originalThree Tricks from Optics
In this contribution we will describe several unusual experiments useful for the purposes of school physics. They are suitable for the students’ individual experiments at school or at home.
1. Refractive index of water (the One line method)
The reader is surely familiar with the fact that the perceived distance of a coin on the bottom of a pool of water is smaller than the real distance. The ratio of the real and perceived distance (when looking from above) equals the refractive index of water (relative to air). This allows us to calculate the refractive index of water. We can use a simple trick to do this calculation with a glass of water.
TRICK no. 1
A glass with a thin, flat bottom is filled with water and placed on top of a sheet of paper we drew a straight line c on. We observe the line through the water column placed from above the glass. The distance of the refracted line c’ is in a smaller depth than the depth of the object (a) underneath the glass.
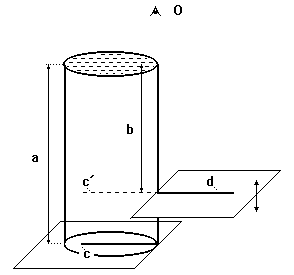
Fig. 1
To determine the perceived distance b, we use another sheet of paper with a line d drawn on it. This we place adjacent to the glass so that both lines (the perceived one in the glass and the real one next to it) form a straight line. To achieve this, we need to place the other sheet of paper a certain distance above the table. We verify the straightness of the lines by observing them from different angles by moving our eye perpendicularly to the lines.
Having achieved the “straightness” we need, we measure the distance a andb, a being the distance between the paper under the glass and the water surface. The distance b is measured from the distance of the paper next to the glass and the water surface. The equation for the refractive index of water is n = a/b. This equals approximately 1.33.
2. Total reflection (mirror from a tic-tac box and a wooden board)
A tic-tac container can be turned into a perfect mirror, thanks to trick no. 2.
TRICK no. 2
The first thing we need for this experiment is a transparent tic-tac box; we remove the label and the detachable top as well. Using a rubber band we attach the box to the end of a plastic ruler P as shown in fig. 2a. The opening of the box should point downwards.
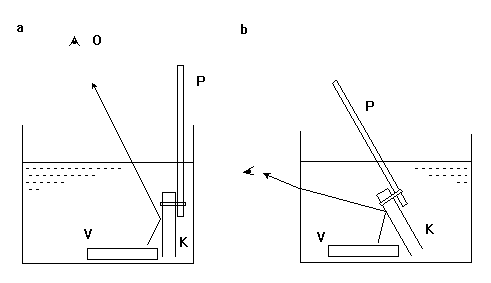
Fig. 2
To achieve the best effect, we put a colourful jar lid V inside a transparent container filled with water. Using a ruler, the upper end of which we hold in our hand, we put the tic-tac container in the water. Air should stay within the container. It’s the air inside the tic-tac container which makes total reflection possible (at certain angles). When looking from above (fig. 2a), the container reflects light like a perfect mirror, and we can clearly see the reflection of the jar lid. The mirroring is similar to a normal pocket mirror which we affix to another ruler for comparison.
Total reflection is responsible for a perfect image of the jar lid and is caused by the light reflecting from the box at an angle greater than the critical angle.
When looking through the side of the water container (and holding the ruler vertically) the tic-tac container seems transparent because in this case the conditions for total reflection are not met.
Demonstration of the experiment
For demonstrational purposes of the experiment a slightly different version of the experiment is more suitable, as shown in fig. 2b. Here the ruler P with the tic-tac container K is tilted and students observe the reflection of the colourful jar lid in the “tic-tac” mirror through the vertical glass pane of the water container. The surface of the box perfectly reflects light only when the ruler is tilted properly. If the ruler is more perpendicular, the box doesn’t reflect and the box appears transparent.
We can observe changes in reflection under different angles.
Of course we can use any box of the right shape instead of the tic-tac container. However, it is important that the container be filled with air when underwater.
Experiment with a cylindrical container
The effects concerning total reflection can also be observed when using a cylindrical container instead of the tic-tac box. The opening of the container should be either underwater or above the water surface. In any case, the container must be filled with air. The curved wall of the container serves us as a cylindrical mirror when looking from above and in it we can see the colourful jar lid placed on the bottom of the water container. However, the experiment is less impressive than with a “flat surface reflection”.
Even a wooden board can be turned into a mirror, with the help of trick no. 3.
TRICK no. 3
If we want to turn a wooden board d into a perfect mirror, we first need to put it inside a transparent document sleeve o so that when placed in water, the wooden board stays dry. When seen from above, we can observe total reflection; we can clearly see the colourful jar lid reflecting from the wooden board, just as it had been seen with the tic-tac box.
If, however, we tilt the object sufficiently, the reflection of the jar lid can be observed by pupils through the side of the water container. As the board is tilted more upright, the reflective properties of the board disappear and we will see only a wooden board.
It should be stressed that it is not the wooden board itself, but actually the air between the board and the document sleeve in which the board is put, which is responsible for the occurring phenomenon. Total reflection takes place at the boundary of air and the document sleeve. The board fulfils only a geometrical role of holding the straight shape of the sleeve. We can actually put any board inside the document sleeve, provided that a small air pocket can be formed between the board and the sleeve.
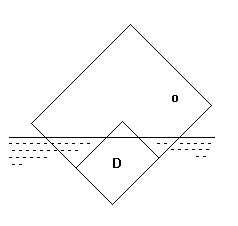
Fig. 3
ADDENDUM Exotic lens – bucket concave lens
We can form a concave lens from water in a small rotating transparent bucket. We rotate the bucket by hanging it onto a thinner string. We twist the upper end with our fingers well, before we lift the bucket from the table. We continue to twist our fingers after lifting the bucket from the table. By doing this we’ll achieve a fast-enough rotation of the bucket and water and a plano-concave water lens will form.
The resulting concave lens has optical properties, which can be observed by placing the rotating water lens above the colourful jar lid and looking through the lens. The image of the jar lid will appear smaller, and this changes as the rotation gets slower.
It should be noted that the experiment with the water lens can be used in hydromechanics as well to demonstrate the properties of rotating liquid and to observe the parabolic profile of the water surface.
References
[1] Baník I. – Baník R.: Niekoľko zaujímavostí z optiky. Zborník “Šoltésove dni - 6”, Bratislava, 14. – 16. December 2000 (in print)