About paper
Czech originalLEDs and Lasers
A laser pointer is an accessible tool and its beam is composed of photons with a wavelength in the interval 630-680 nm. In supplier’s catalogues there are laser diodes with expected wavelength λ = 655 nm for sale at a price of about 550 Kč (€20), and in the marketplace, laser-toys can be found for 210 Kč (€8) or less. What a bargain!
Light-emitting diodes belong to a family of semiconductor devices that students are familiar with thanks to a bunch of laboratory equipment and consumer electronics. Recently, sought after alternative sources of energy are also represented within this family: photovoltaic cells are nothing else than semiconductor diodes. If you are unfamiliar with solar panels, the concept is simple: “semiconductor diode + light = source of electric energy”.
The condition naturally is that the light would penetrate into the diode. Older germanium point-contact diodes (from GA 201 to 205) were encased in glass containers, additionally silicon Zener diodes from 1NZ70 to 8Nz70 are encapsulated in metal, but anodes are led out through glass bushings, and finally all LEDs are transparent or at least translucent.
To perform the first experiment, we use a source of light – an overhead projector, METEX 3850 (or equivalent), digital multimeter and set of diodes.
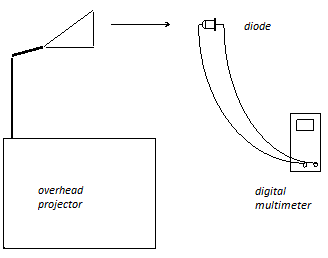
Moving a diode closer to the centre of the overhead projector lens, we obtain quite interesting values of voltage due to the high input resistance of the voltmeter (12 MΩ) which may be regarded as an electromotive force.
| Model of diode |
Type of diode |
emf [mV] |
| GA205 |
germanium point-contact |
57 |
| 6NZ70 |
silicon junction |
330 |
| LQ1102 |
LED red 660 nm |
1290 |
| LQ1412 |
LED yellow 587 nm |
1506 |
| LQ1711 |
LED green 565 nm |
1602 |
Table 1: Electromotive forces of diodes
When a diode is being drawn away from the lens, the voltage magnitude starts to decline and vice versa. Can it be infinitely large or is it physically limited by some specific value? Why do different diodes give different values of emf? The principle behind the generation of this voltage provides the answers.
In the PN junction, unexposed to the light, a space charge region H is created without free charge carriers and an electric field with the intensity of Ed due to the diffusion of electrons from the N region into the P region. An absorbed photon generates the electron-hole pair and the diffusion region splits them: the hole is pushed to the left and the electron to the right.
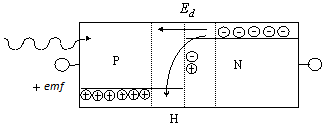
The electric field created by such charge transfer is polarised in the opposite direction to the diffusion field. Thus the electromotive force of a photodiode can not be larger than the band gap of semiconductor in use.
The measurement is affected by the colour of the epoxy cases belonging to the LQ models. Measurements performed on the LEDs enclosed in transparent and almost colourless cases allow this distortion to be excluded. The following diodes satisfy this condition.
| Model |
emf (V) METEX 3850 12 MΩ |
emf (V) MIT 390 >1000 MΩ |
IF (μA) MIT 390 |
I0 (nA) under Uak = -5 V MIT390 |
| L-538SRC/E red |
1.57 |
1.57 |
600 |
0 |
| L-HLMP3850 yellow |
1.58 |
1.58 |
80 |
0 |
| L-HLMP3950 green |
1.66 |
1.63 |
20 |
0 |
| L-53MBDL blue |
0.02 |
0.9 |
0 |
2 |
Table 2: Influence of measuring instrument and colour of epoxy LED cases
Within the blue diode we would expect the largest electromotive force, which we could not measure with METEX. We are able qualitatively to explain why it is so.
The table above presents the values of the electromotive force measured by multimeter MIT 390 whose input resistance on the given range is higher than 1 GΩ.
In this case the blue diode also generates emf = 0.8 V, which is less than we expected.
Dependence of emf on the light intensity is caused by the presence of minority charge carriers – electrons in p-type semiconductor and holes in n-type. The electromotive force is theoretically given by the equation \[ U_e = \frac{kT}{e} \ln \left( 1+ \frac{j_f}{j_s} \right),\] where k is Boltzmann constant, T the thermodynamic temperature, e the charge of an electron, jf the current density generated by split electron-hole pairs after absorption of photons and js the density of the saturation current caused by minority carriers. The saturation current appears as a reverse current in every semiconductor diode. (See Šalimovová, K. V.: Fyzika polovodičov, ALFA, Bratislava 1978)
The photo-generated current (measured with the help of MIT 390) is very small and even immeasurable in the blue diode. On the other hand the reverse current in the blue diode is substantially higher compared to the others, hence the electromotive force is very small.
Instead of the overhead projector we use the laser to illuminate the PN junction. Values achieved for the electromotive forces across the germanium diode, the silicon diode and the red LED would be less than in the previous experiment. For the yellow and green LEDs the result would be almost zero, although the laser beam clearly illuminates the crystal in the diode. The cause lies in the energy of photons and the electronic band structure of semiconductor crystals. During photon absorption in the semiconductor, the electron-hole pair is able to form only if its energy is greater than the band gap (without consideration of the substrate bands or other interactions leading to the electronic band structure disturbances).
It is necessary that h·f ≥ ΔE.
| Model |
emf (V) METEX 3850 |
| L-538SRC/E red |
1.54 |
| L-HLMP3850 yellow |
0.015 |
| L-HLMP3950 green |
0.006 |
| L-53MBDL blue |
0.000 |
Table 3: Electromotive forces of LEDs illuminated by laser
The graph below shows the band gap values (in electronvolts) of semiconductors used for diode production and the wavelengths corresponding to those energies.
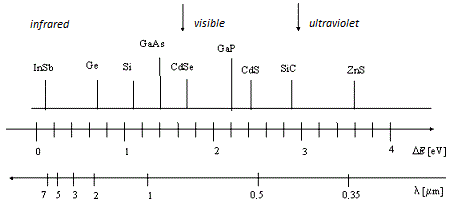
The graph shows that the photon with wavelength 655 nm will successfully generate charge carriers in the red LED but not in yellow or green where its energy is insufficient. For each diode there exists the long wavelength limit, over which photogenerated current and electromotive force is not generated.
This limit is possible to find, at least qualitatively, in the following experiment:
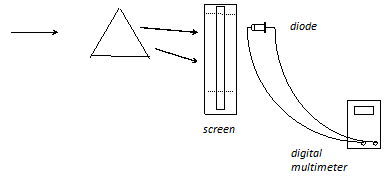
We use a prism to disperse the light into its spectral components, creating the spectrum on the screen. The light of specific wavelengths passes through the slits in the screen to illuminate the diode connected to the voltmeter. Moving the diode from the ultraviolet to infrared light we can determine where the voltage across the diode disappears.
References:
[1] Eckertová L.: Fyzikální elektronika pevných látek UK Praha 1992