About paper
Czech originalWavelength of Light in Water - Easy Measurement Using a CD
It is easy to measure the wavelength of light not only in air, but also in water using a CD. The appropriate methods of measuring the wavelength of light in air are described in papers [1. 2]. In this paper, we focus on how to measure it in water.
For optical measurements with a CD we use the fact that the recording surface represents a good-quality reflective optical grating. The record of a CD has a character of spiral track with a density of 625 tracks on 1 mm. The relevant lattice constant of the CD reflective grating is thus O1O2 = 1.6 micrometres.
General remarks on measuring the wavelength of light using a reflective grid
If the reflective optical grating with the lattice constant O1O2 is illuminated by a monochromatic ray with the incidence angle α, the reflected light waves will be amplified only in such directions, for which the path difference δ of the rays diffracted on two adjacent “points” of diffraction on the grid is equal to an integer multiple of the wavelength λ, that is if δ = i·λ. This condition is met only for the rays that propagate from the point of reflection with the reflecting angles βi. If we measure the angle βi of the appropriate i-th non-zero interference maxima, we can determine the wavelength of light in the given environment based on the formula [1, 2] \[ \lambda = \left| \frac{O_1O_2}{i} (\sin \beta_i - \sin \alpha ) \right|. \]
The incidence angle α is always considered positive, or zero. Yet, the angle βi may reach positive and negative values. The angles βi in the half plane (with respect to the incidence perpendicular), in which the mirror-reflected ray is located, are positive, the angles in the opposite half plane are negative.
Our special case
In view of the arrangement which we will use in the measurement of the wavelength of light in water, a special case of the current configuration is such that we monitor the light reflected in the opposite direction to the direction of the incident ray. If we observe the first interference maximum under the angle β = βi = - α, the corresponding relation for wavelength will be \[ \lambda = \left|O_1O_2 (\sin\alpha - \sin (-\alpha)\right| = \left|2O_1O_2 \sin \alpha\right|. \]
Similarly, for the i-th interference maximum we get the formula \[ \lambda = \left|\frac{2}{i} O_1O_2 \sin \alpha\right|. \]
If the source emits white light, the angles corresponding to each maximum are different for each color. The color effects appear. The above mentioned relations help us to determine the wavelength for different colors.
Measurement in water
The overall configuration in the measurement is shown in Fig.1. The CD (or a piece of a CD) is immersed in water in a shallow container N. The container is tilted to one side during the measurement.
The light beam is emitted from a small light-bulb and propagates down vertically perpendicularly to the water surface. Without any change it propagates further, until it touches the CD recording surface. The lines of the reflective optical grating in the point of incidence of the beam on the CD are perpendicular to the plane of the drawing. The eye of the observer follows a chosen part of the CD as we tilt the container. If the CD is horizontal (at the beginning), in the vertical view the observer sees two identical images of the point emitter - one image is a result of the light reflecting on the water surface, the second is the result of the light reflecting on the CD like in a mirror (zero maximum).
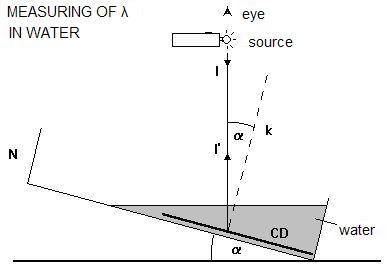
Fig. 1
If we tilt the container, the color of the CD in observed place gradually changes. At a certain inclination of the CD, the observed part of the CD gains a color shade corresponding to our monitored color (e.g. red). In this situation, we measure the angle α of inclination of the container, which is corresponding to the first interference maximum of the given light wave in water. (This angle would be exactly the same even if we performed the whole measurement directly in water, because the water-air interface in our situation does not change the direction of the beam.) The wavelength of light of the given color in water can be determined using the above mentioned relation valid for our special case \[ \lambda_V = \left|2 O_1O_2 \sin \alpha\right|. \]
In a similar way, we can measure the angle α = -βi of the inclination of the container for the i-th interference maximum, while for the wavelength of light in water applies \[ \lambda_V = \left|\frac{2}{i} O_1O_2 \sin \alpha\right|. \]
Literature:
[1] Baník I., Baník R.: Netradičné spôsoby pozorovania interferenčných optických javov. Zborník konf.
[2] Didfyz 96, Natural sciences education for the 21 st centaury, Račkova Dolina 23. až 26. október 1996, s. 104–111
[3] Zámečník J., Baník I. a kol.: FYZIKA – Návody na laboratórne práce, STU Bratislava, 1996, 108 s.
[4] Baník I.: Meranie vlnovej dľžky svetla vo vode pomocou CD-platne, Proceedings: Physical properties of materials, International Workshop, SUT Bratislava 2000, s. 119