Jaké deformační křivky používají fyzikové

Zdeněk Drozd, KDF MFF UK, Ke Karlovu 3, 121 16 Praha 2

Velice zajímavou částí fyziky materiálů je výzkum plastické deformace. V tomto případě je třeba získat deformační křivku, v níž bude právě jenom plastická deformace. Elastickou deformaci do křivky nezahrneme. Jak se to dělá? Pomocí deformačního stroje získáme hodnoty deformační síly a času, který uplynul od začátku deformování. Pokud tyto hodnoty vyneseme do grafu, získáme takovouto křivku:

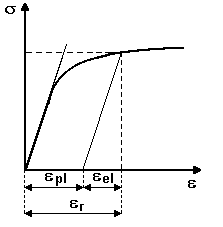
V obrázku je naznačeno oddělení elastické a plastické deformace. Písmeno k označuje směrnici lineární části křivky. Co to je směrnice možná víte z matematiky. Pokud ne, tak směrnice udává „stoupání přímky“. Můžete ji určit způsobem naznačeným na následujícím obrázku:

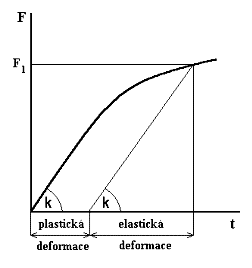
Skutečnému napětí (smluvní napětí se ve fyzice příliš nepoužívá) jsou přiřazeny hodnoty plastické deformace, která se počítá podle vztahu:

,

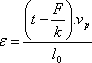kde t je čas od začátku deformování, v_p rychlost pohybu příčníku, k směrnice elastické části, F zatěžovací síla, l₀ počáteční délka vzorku.

Deformační křivka plastické deformace má tedy na vodorovné ose plastickou deformaci e a na svislé ose skutečné napětí.

Poznámka: Fyzikové používají tzv. skutečnou deformaci. Křivky potom znázorňují závislost skutečného napětí na skutečné deformaci. Skutečnou deformaci zde ale nebudeme zavádět. Potřebovali bychom k tomu totiž trošku složitější matematiku. Jenom pro úplnost – skutečná deformace v tahu se počítá podle vzorce ε = ln (1+ε_r), kde ε_r je relativní prodloužení.