Fyzika materiálů
… a co s ní na gymnáziu?
Zdeněk Drozd, KDF MFF UK, Ke Karlovu 3, 121 16 Praha 2
Úvod
Fyzika na gymnáziu – to je téma k dlouhým diskusím. Můžeme se zamýšlet nad metodami výuky, nad obsahem učiva, nad tím jak ukázat, že fyzika je věda užitečná v našem každodenním životě a že by nám mohla pomáhat při řešení problémů, s nimiž se setkáváme. Student gymnázia, který nemá s fyzikou žádné vážné úmysly, protože oblastí jeho zájmu jsou např. tzv. společenské vědy, nemá příliš mnoho příležitostí seznámit se s praktickými aplikacemi fyziky. Záběr učiva fyziky je totiž příliš velký – od mechaniky, přes základy termodynamiky, elektřinu a magnetismus, optiku až k základům moderní astrofyziky, kvantové a relativistické fyziky. Všechny tyto fyzikální oblasti sice mají obrovské aplikace v technice, která ovládá náš svět (astrofyzika a relativistická fyzika jsou na tom ovšem s běžnými aplikacemi zatím ještě trochu hůře), učitel je ale většinou rád, že vůbec stihne probrat teoretické základy jednotlivých témat. Jinak je tomu na „průmyslovkách“. Tam se žáci aplikacím věnují – probírají ale pouze některé pro jejich budoucí praxi důležité partie fyziky.
Laická veřejnost občas argumentuje tím, že na gymnáziu se učí většinou fyzika 17. – 19. století, a na moderní partie už nezbývá čas. To samozřejmě může říct jenom ten, kdo fyzice nerozumí a neví, že bez znalostí základů mechaniky, optiky, elektřiny a magnetismu to ve fyzice jaksi nejde.
Je mnoho oblastí, které by si asi zasloužily větší pozornost, protože jsou dnes základními kameny moderní techniky. Jako příklad nás asi nejprve napadne elektronika. Nikdo zřejmě nepochybuje o jejím významu v dnešním moderním světě – ale že by se jí gymnazisté v rámci výuky fyziky příliš zabývali – to asi říct nemůžeme. Jinou oblastí, která nás pravděpodobně hned nenapadne, je fyzika materiálů. Pokrok civilizace bez nových materiálů je nemyslitelný. Ostatně to, jaký význam měly materiály v dějinách lidské civilizace, už dávno vědí historikové. Ti dokonce jednotlivé vývojové etapy lidstva pojmenovali podle dominujících materiálů, které lidstvo v té které době používalo – doba kamenná, doba bronzová, doba železná. (Co je asi dnes? Že by doba plastová?)
Každý, kdo něco kritizuje, by měl přijít s námětem na řešení diskutovaného problému. To si samozřejmě uvědomuji i já, a proto nebudu hlásat, že do fyziky na gymnáziu se musí zařadit téma fyzika materiálů na úkor něčeho jiného, nebo dokonce bez toho, že by se jiné téma omezilo. No a učitelé ať se pěkně snaží a „nacpou“ toho do hlav ubohých studentů ještě více. Už tak je toho v gymnaziální fyzice dost. Vzhledem k počtu hodin fyziky bych spíše měl říct, že je toho více, než je zdrávo. Co tedy s tím? Učitelé by měli k výuce přistupovat s rozumem, vybrat minimum základních poznatků, které by měli zvládnout všichni žáci. Měli by ovšem také poznat, kdo ze studentů má k fyzice blíže, a těm se věnovat více. Dávat jim náměty k práci navíc – např. k domácím experimentům. Poradit jim vhodnou literaturu, webové stránky, ale také jim např. umožnit účastnit se mimoškolního fyzikálního dění – existují různé kroužky a kurzy pro středoškoláky (dnes i distanční kurzy). Aktivní učitel fyziky by si podle mě měl pečovat o fyzikální výkvět své školy a pro své talentované žáky zřídit nějaký fyzikální klub. Žáci to jistě uvítají a učitel sám bude mít radost z práce se skupinkou fyzikálních nadšenců.
Právě pro takové aktivity je určen můj příspěvek. Námět, jak začít s fyzikou materiálů, v tomto případě s tématem mechanické vlastnosti materiálů. Uvedu stručný úvod do problematiky a ukázku toho, jak ji ověřit experimentem.
Deformace materiálů prakticky
K základním vlastnostem materiálů patří jejich deformační chování. Naznačíme si zde základy teorie pružné a plastické deformace (to jsem ale řekl příliš troufalou věc – ony by ty základy vydaly na tučnou knihu). Nechci ale sepsat několik vzorců a k nim připojit vysvětlující výklad. Ukážu, jak se k tomuto tématu postavit při výuce. Celým problémem nás budou provázet jednoduché experimenty s modelářskou gumou. Dám zde námět, jak studenty provázet tímto učivem s tím, aby měli dost příležitostí sami objevovat nové poznatky. Rozumějte tomu ale správně – nepůjde o objevy něčeho nového, neznámého. Půjde o objevování věcí známých už dávno (i stovky let). Pro studenty to ovšem nové věci většinou budou, a pro ně to tedy budou objevy. Dopřejte svým žákům radost z objevování!
Motivační pokus
Pro každou skupinu žáků připravte několik závažíček o hmotnosti 50 g (aspoň 10), nebo 100 g (aspoň 5). Závažíčka musí mít na obou stranách háčky, aby se mohla věšet jedno na druhé (používají se při pokusech z mechaniky). Pokud jich máte málo, sežeňte si dětské kyblíčky na písek (lehké - umělohmotné). Ty budete plnit vodou a používat jako závaží. Ke každému kyblíku budete potřebovat ještě odměrku na vodu (50 ml). Tu si žáci mohou vyrobit např. z plastového kelímku od jogurtu.
Dále budete potřebovat modelářskou gumu. Stačí vázací guma na křídla modelů. Mám vyzkoušeno, že vhodný průřez je 6 mm x 1 mm. Ta se prodává např. v 5 m balení asi za 30 Kč. Každá skupina bude potřebovat necelý metr gumy.
Vyhlédněte si vhodné místo, kam lze gumu přivázat - zábradlí, futra dveří (na ty je možné přichytit truhlářskou svěrku a máte výborný závěs). Zavěšení gumy nějak vymyslete. Asi půl metru pod závěsem udělají žáci na gumě smyčku, do které budou zavěšovat závaží. Budou-li používat kbelík, přivážou jej také asi půl metru pod závěs. Počítejte s tím, že guma se při pokusu protáhne víc než na dvojnásobek. Musí být tedy přivázaná dostatečně vysoko.
Každá skupina změří počáteční délku gumy l0 mezi uzlíkem u závěsu a uzlíkem u smyčky pro závažíčka (u ucha kyblíku). Na gumu postupně přidávají závažíčka a do tabulky zapisují hmotnost zátěže a odpovídající zatěžující sílu a samozřejmě také délku gumy (musí ji stále měřit mezi uzlíky). Vypočítají ještě prodloužení gumy Δl = l-l0.
Pokud používáte variantu „zatěžovacího kyblíku“, přilévejte do něj vodu po 50 ml. (100 ml odpovídá přibližně 100 g a to představuje zatěžovací sílu přibližně 1 N.)
Zatěžování probíhá tak dlouho, až se guma protáhne aspoň na dvojnásobek počáteční délky.
Dále žáci sestrojí graf závislosti síly potřebné k natažení gumy o Δl na tomto prodloužení. (Na svislé ose bude F na vodorovné Δl.)
Položte otázku: „Myslíte si, že by graf a tabulka, které jste získali, mohly být dostatečným popisem vlastností zkoumané gumy? Nebo by to chtělo nějaké vylepšení?“
Výsledky pokusu mohou žáci zapisovat do následující tabulky.
Tabulka 1
| m / g |
|
|
|
|
|
|
|
|
|
|
|
| F / N |
|
|
|
|
|
|
|
|
|
|
|
| l / cm |
|
|
|
|
|
|
|
|
|
|
|
| Δl / cm |
|
|
|
|
|
|
|
|
|
|
|
vysvětlivky k tabulce:
m - hmotnost zatěžovacích závaží (nebo kyblíku s vodou)
F - zatěžovací síla
l - délka gumového vlákna
Δl - prodloužení gumového vlákna
Pružná deformace
Popisovat deformaci gumového vlákna nebo jiného materiálu pomocí jeho prodloužení není příliš šikovné. Představte si, že máte dvě vlákna stejného průřezu, jejichž délky jsou 10 cm a 1 m. Když na každé z nich pověsíte závaží 100 g, jejich protažení nebude stejné. Delší vlákno se protáhne víc. Kdybyste ale vypočítali, o kolik procent se každé z nich prodloužilo, dostali byste srovnatelné údaje. Proto se deformace těles popisuje veličinou, která má název relativní prodloužení. To lze vypočítat jako poměr prodloužení a počáteční délky zatěžovaného vzorku (gumy). Často se označuje εr. Pro relativní prodloužení platí vztah
![]() .
.
Udávat hodnoty zatěžovací síly (tahové síly) také není nejvhodnější. Kdybyste stejnou silou zatěžovali vlákna různého průřezu, bylo by relativní prodloužení pro každé z nich jiné. To je nešikovné. Určuje se proto, jaká síla působí kolmo na jednotku průřezu zatěžovaného tělesa. V našem případě by bylo jednoduché spočítat, jak velká síla působí na 1 mm2. Chceme-li používat jednotky soustavy SI, musíme učit sílu (v newtonech) působící na 1 m2 průřezu gumového vlákna. Tím získáme tzv. tahové napětí, které se měří v N/m2 neboli v Pa. Obvykle se značí řeckým písmenem σ. Velmi často se jako jednotka napětí používá MPa. Je užitečné pamatovat si, že 1 MPa odpovídá zatížení 1 N na 1 mm2.
Už roku 1676 zjistil Robert Hooke, že pro mnoho materiálů platí při zatěžování jednoduchý zákon – napětí je přímo úměrné relativnímu prodloužení. Hookův zákon platí ale jenom do určitého zatížení, dokud napětí nedosáhne jisté meze. Tato mez se nazývá mezí úměrnosti. Nedojde-li k jejímu překročení, vrátí se po odtížení deformovaný vzorek materiálu do původního tvaru (guma bude mít po sejmutí závažíček původní délku – vyzkoušejte to). Když překročíme mez úměrnosti, dojde k nevratné deformaci materiálu.
Hookův zákon můžeme vyjádřit pomocí rovnice
σ = E εr.
Konstanta úměrnosti E se nazývá modul pružnosti (v tahu). Její jiný název je Youngův modul. Chová-li se materiál při zatěžování tak, že je splněn Hookův zákon, hovoříme o pružné (elastické) deformaci. Některé látky se podle Hookova zákona nechovají nikdy, např. modelína, ale většina materiálů jej až do určitého napětí splňuje.
No a na závěr tohoto krátkého povídání ještě jedna informace. Gumové vlákno se chová při zatěžování jinak než třeba drát. Ten se při jistém napětí začne plasticky deformovat (někdy se říká, že „teče“). U gumy je tomu naopak. Přesáhne-li deformační napětí určitou mez, guma se téměř přestane protahovat (a při zvyšování zatěžovací síly po nějaké době praskne). Je to dáno odlišnou vnitřní stavbou gumy a kovů (drátu v našem příkladu).
Další pokus
Guma je elastický materiál. To znamená, že když ji natáhnete a opět povolíte, vrátí se do původního tvaru - takovou zkušenost jistě máte. Z fyzikálního hlediska ale to, že je guma (nebo jiný materiál) elastická, znamená, že pro ni platí Hookův zákon. Vyzkoušejte to.
Připravte si posuvné měřítko (šupleru) a proveďte se žáky ještě jeden pokus. Opět při něm budou zatěžovat gumu. Tentokrát ale budou ještě měřit a do tabulky zapisovat příčné rozměry gumy (a, b). Z nich vypočítají aktuální průřez gumového vlákna (S) při každém zatížení.
Nyní mohou žáci vypočítat napětí v gumě a relativní prodloužení, která odpovídají jednotlivým prodloužením. Jsou dvě možnosti. Počítat napětí tak, že dělíme zatěžovací sílu počátečním průřezem gumy – získáme tzv. smluvní napětí, nebo použijeme pro výpočet napětí aktuálních hodnot průřezu při každém zatížení – získáme tzv. skutečné napětí. Žáci spočítají obě hodnoty napětí a sestrojí graf závislosti těchto napětí na relativním prodloužení. Takovému grafu se říká deformační křivka. Při pokusu je možné používat následující tabulku (je nutné poznamenat si také počáteční hodnoty l0, S0):
Tabulka 2
| m / g |
|
|
|
|
|
|
|
|
|
|
| F / N |
|
|
|
|
|
|
|
|
|
|
| a / mm |
|
|
|
|
|
|
|
|
|
|
| b / mm |
|
|
|
|
|
|
|
|
|
|
| S / mm2 |
|
|
|
|
|
|
|
|
|
|
| Δl / mm |
|
|
|
|
|
|
|
|
|
|
| εr |
|
|
|
|
|
|
|
|
|
|
| σsml / MPa |
|
|
|
|
|
|
|
|
|
|
| σskut / MPa |
|
|
|
|
|
|
|
|
|
|
Následující obrázek ukazuje, jak mohou oba grafy vypadat.
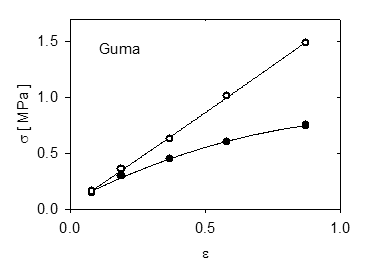
Obr. 1: Graf závislosti smluvního napětí (plné kroužky) a skutečného napětí (prázdné kroužky) na relativním prodloužení gumy.
Je vidět, že o Hookově zákonu lze mluvit v případě skutečného napětí. Žáci také mohou určit modul pružnosti gumy v tahu a porovnat jej s jinými materiály. Můžeme diskutovat o tom, co nám vlastně modul pružnosti říká.
Naznačeným postupem jsme zavedli nejdůležitější veličiny, které se používají pro popis deformace tělesa (vzorku materiálu). Zavedení veličin není úplné. Chybí skutečná deformace. Pro její pochopení je ale nutné umět integrovat, proto ji v tomto textu vynechávám.
Pokusy z gumou, které zde byly popsány, jsou jednoduché na provedení a samozřejmě, že výsledky, které pomocí nich získáte, jsou nepřesné. Jejich úkolem je oživit výuku nového tématu. Při vyhodnocování jsme ale použili stejný postup, jaký používají materiáloví fyzikové. Chcete-li svým žákům poskytnout základní informace o tom, jak se provádí skutečné deformační zkoušky, a chcete-li krátké souhrnné články o deformačních křivkách „klikněte“ na následující hesla:
• deformační křivky v technické praxi
Závěr
Tento příspěvek ukazuje, jak je možné přistoupit na gymnáziu k základnímu tématu fyziky materiálů – k deformačním vlastnostem materiálů. Je samozřejmě možné navázat dalšími tématy. To ale záleží na jednotlivých učitelích a jejich zájmech. Podobně je možné zpracovat i jiné partie fyziky, na které se v běžné výuce nedostane. Každé nové téma, které studentům přiblíží, jak lze fyziku aplikovat v praxi, prokáže výuce fyziky jako celku dobrou službu.